Anticlessidra
L’anticlessidra è un solido geometrico ottenuto sottraendo due coni identici da un cilindro equilatero che circoscrive una sfera.
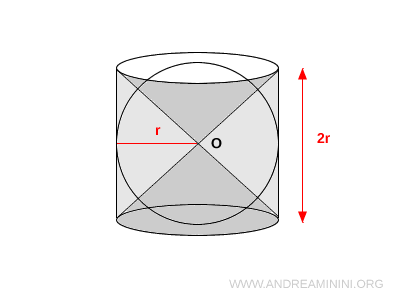
Il risultato è un solido apparentemente semplice ma con proprietà geometriche interessanti sia nel volume che nella simmetria.
Come costruire un'anticlessidra
Si parte da una sfera di centro O e raggio $R$.
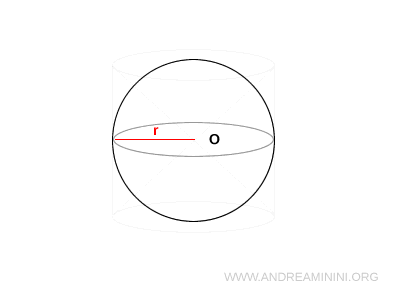
A questa sfera circoscrivo un cilindro equilatero, cioè un cilindro il cui diametro di base $ r $ è uguale all’altezza $ h $, quindi:
- Altezza del cilindro: $h = 2R$
- Raggio di base del cilindro: $r = R$
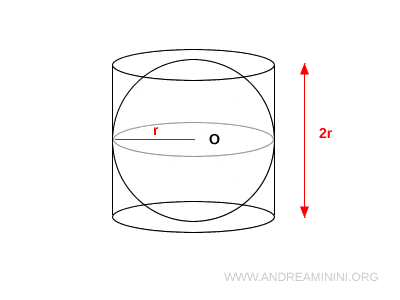
A questo punto, costruisco due coni con vertice in O e le basi coincidenti con le basi del cilindro.
Ogni cono ha quindi:
- Altezza: $R$
- Raggio di base: $R$
Infine, sottraggo questi due coni dal volume del cilindro.
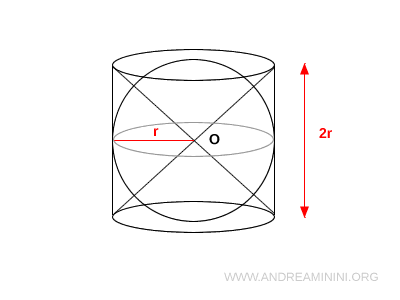
Il solido che ottengo è detto anticlessidra ed è la differenza tra il cilindro e i due coni.
Somiglia a un cilindro scavato alle estremità da due coni uguali, uno capovolto rispetto all’altro.
Volume dell’anticlessidra
L’anticlessidra ha lo stesso volume della sfera inscritta nel cilindro.
Il volume del cilindro equilatero è:
$$ V_{\text{cil}} = \pi R^2 \cdot 2R = 2\pi R^3 $$
Il volume di un cono con raggio $R$ e altezza $R$ è:
$$ V_{\text{cono}} = \frac{1}{3} \pi R^2 \cdot R = \frac{1}{3} \pi R^3 $$
Siccome ci sono due coni, il volume totale da sottrarre è:
$$ 2 \cdot V_{\text{cono}} = 2 \cdot \frac{1}{3} \pi R^3 = \frac{2}{3} \pi R^3 $$
Quindi, il volume dell’anticlessidra è:
$$ V_{\text{anticlessidra}} = V_{\text{cil}} - 2 \cdot V_{\text{cono}} = 2\pi R^3 - \frac{2}{3} \pi R^3 = \frac{4}{3} \pi R^3 $$
Il volume dell’anticlessidra è esattamente uguale al volume della sfera di raggio $R$:
$$ V_{\text{sfera}} = \frac{4}{3} \pi R^3 $$
Esempio
Se la sfera ha raggio $R = 3$ cm, il volume dell’anticlessidra sarà:
$$ V = \frac{4}{3} \pi (3)^3 = \frac{4}{3} \pi \cdot 27 = 36\pi \approx 113,1 \, \text{cm}^3 $$
Quindi, l'anticlessidra evidenzia le relazioni tra figure tridimensionali.
Pur essendo costruita a partire da forme semplici, il suo volume coincide perfettamente con quello della sfera circoscritta, un risultato non ovvio ma rigorosamente dimostrabile.
Nota. L'anticlessidra può essere usata per introdurre il principio del confronto dei volumi, utile nei problemi di integrazione e nella comprensione del metodo degli indivisibili, già utilizzato da Archimede. Ad esempio, se divido i solidi in parti elementari come sezioni, segmenti, ecc. e li confronto con quelli di un altro solido, se ogni “pezzo” corrisponde, allora anche il volume totale dei due solidi è lo stesso, ossia i solidi sono equivalenti in volume. E' la base del principio di Cavalieri.
Dimostrazione
Considero un cilindro equilatero di altezza $2r$ e raggio $r$, poggiato su un piano $p$, una sfera inscritta nel cilindro e due coni opposti che hanno il vertice nel punto $ O $ (centro della sfera) e le basi coincidenti con il cilindro.
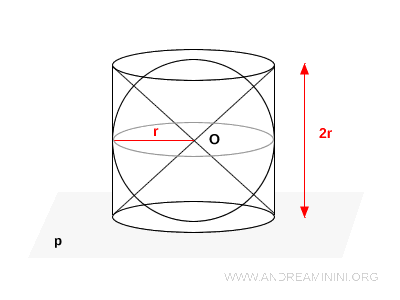
Taglio il cilindro con un piano parallelo $p'$, posto a distanza $h$ dal centro $O$ della sfera inscritta nel cilindro.
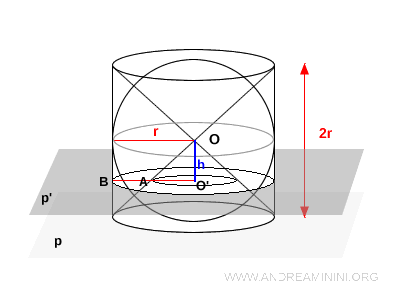
L'intersezione del piano $p'$ con il cono (parte dell’anticlessidra) è una circonferenza di raggio $h$. Infatti, il triangolo $OO'A$ è un triangolo rettangolo e isoscele, poiché $ OO' = O'A $ essendo un cilindro equilatero, quindi i cateti misurano entrambi $h$, ossia $O'A = h$.
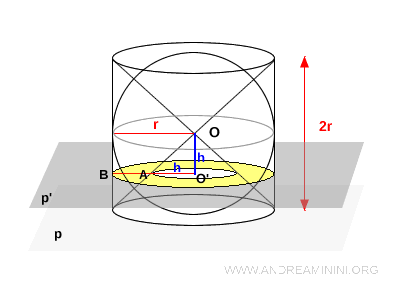
L'intersezione del piano $p'$ con l'anticlessidra è quindi una corona circolare: il raggio esterno è $r$ (quello del cilindro), il raggio interno è $h$ (quello della sezione del cono).
L’area di questa corona è:
$$ A_c = \pi r^2 - \pi h^2 = \pi (r^2 - h^2) $$
Ora considero la sfera inscritta nel cilindro.
Il piano $p'$ interseca la sfera in un cerchio. Il raggio di questo cerchio è $O'C$, dove $ C $ è un punto di intersezione sulla superficie della sfera.
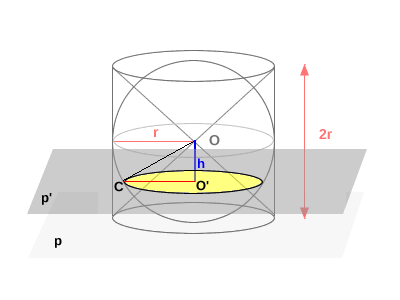
Il triangolo $O'OC $ è rettangolo in $ O' $, quindi posso applicare il teorema di Pitagora:
$$ O'C^2 = OC^2 - OO'^2 = r^2 - h^2 $$
L’area del cerchio intersezione tra la sfera e il piano $p'$ è:
$$ A_s = \pi \cdot O'C^2 = \pi (r^2 - h^2) $$
Quindi, l’area della sezione orizzontale della sfera coincide con quella della sezione dell’anticlessidra, per qualunque piano $p'$ parallelo a $p$.
Per il principio di Cavalieri, due solidi con la stessa altezza e con sezioni parallele congruenti hanno lo stesso volume.
Di conseguenza: l’anticlessidra e la sfera hanno lo stesso volume.
E così via.
