L'estensione dei solidi
Nella geometria solida l’estensione di un solido rappresenta la quantità di spazio occupato da un corpo tridimensionale.
Non è qualcosa che si misura direttamente come la lunghezza o l’area: è un concetto primitivo, cioè accettato senza bisogno di una definizione formale. Si può comprendere attraverso l’intuizione e l’esperienza.
Ad esempio, quando osservo un oggetto tridimensionale, come una scatola, una sfera o una piramide, la prima cosa che percepisco è lo spazio che occupa. Quanto è "grande" o quanto è "piccolo".
Questo spazio occupato non è solo una misura fisica, ma un concetto fondamentale per definire il volume, l'equivalenza e la congruenza tra i solidi.
E' intuitivo che due oggetti sono estesi allo stesso modo se occupano lo stesso volume nello spazio, anche se hanno forma diversa.
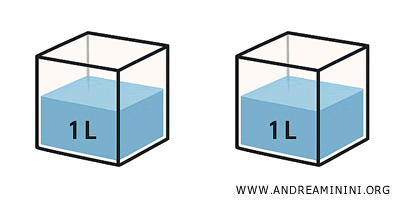
Esempio. Un litro d’acqua versato in una bottiglia, in un cubo o in una sfera riempie ciascun contenitore completamente. I contenitori, pur con forme diverse, hanno la stessa estensione.
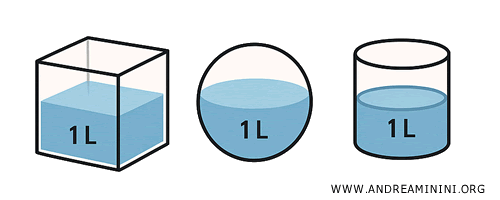
In geometria, si usa il volume per quantificare e confrontare estensioni. Ma attenzione: il volume non dipende dalla forma, solo dalla quantità di spazio occupato.
Equivalenza tra solidi
Due solidi A e B si dicono solidi equivalenti se hanno la stessa estensione. $$ A \doteq B $$ Dove $ \doteq $ è il simbolo dell'equivalenza.
Questa relazione è molto simile a quella che si applica ai numeri o agli insiemi, e soddisfa tre proprietà fondamentali:
- Riflessiva: ogni solido è equivalente a sé stesso.
- Simmetrica: se A è equivalente a B, allora B è equivalente ad A.
- Transitiva: se A è equivalente a B e B è equivalente a C, allora A è equivalente a C.
Queste proprietà definiscono una relazione di equivalenza.
Pertanto, l'equivalenza tra solidi è una relazione di equivalenza che suddivide i solidi in classi di estensione, cioè insiemi di solidi che occupano la stessa quantità di spazio.
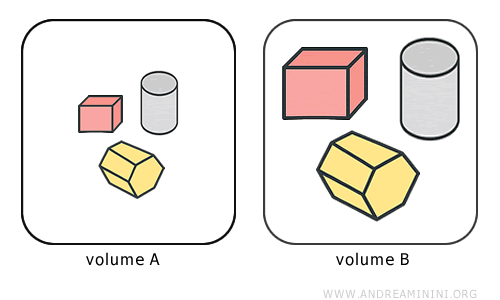
Il volume è una misura numerica dell’estensione di un solido. Quindi, le classi di estensione sono associate al volume degli oggetti.
Come capire se due solidi sono equivalenti
Generalmente i solidi vengono suddivisi in unità di volume più piccoli e riassemblati.
Ad esempio, se ho un solido e lo divido in quattro cubi più piccoli ottengo quattro solidi che posso riassemblare in modo diverso incastrandoli tra loro.
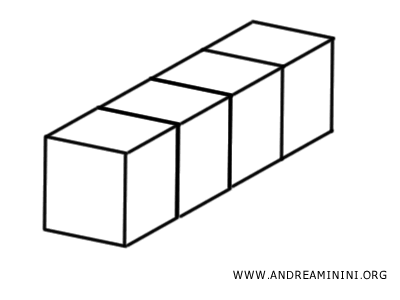
Il nuovo solido ha la stessa estensione del solido originale, perché ho solo riorganizzato lo spazio, non ho aggiunto né tolto nulla. Quindi i due solidi sono solidi equivalenti e hanno lo stesso volume.
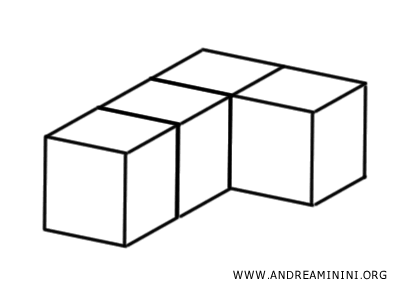
Tuttavia, la forma del nuovo solido è cambiata, quindi i due solidi non sono congruenti.
E' un po' come giocare con i mattoncini. Se uso sempre lo stesso numero di mattoncini per costruire qualcosa, il volume di ciò che costruisco è sempre lo stesso indipendentemente dalla forma.
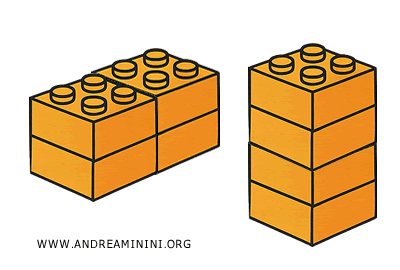
La differenza tra congruenza ed equivalenza
La congruenza e l'equivalenza sono due concetti distinti:
- Solidi congruenti: hanno la stessa forma e dimensione. Quindi, sono sempre equivalenti.
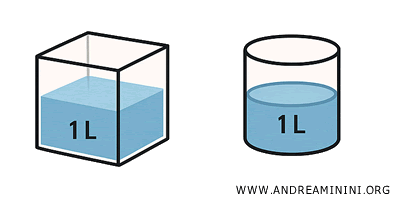
- Solidi equivalenti: hanno lo stesso volume, ma non necessariamente la stessa forma. Quindi, non sempre congruenti. Ad esempio, un cilindro e un prisma possono avere la stessa altezza e lo stesso volume, ma forme completamente diverse. Sono equivalenti, ma non congruenti.
Comprendere l’estensione dei solidi è essenziale per costruire il concetto di volume e per confrontare figure tridimensionali nella geometria.
È ciò che ci permette di dire che una bottiglia da un litro ha la stessa capacità, a prescindere dalla sua forma.
In conclusione, l’estensione non si vede, ma si misura attraverso il volume. E proprio come due libri di forme diverse possono occupare lo stesso scaffale, due solidi diversi possono riempire lo stesso spazio.
E così via.
