Parallelepipedo
Il parallelepipedo è un prisma in cui le basi sono due parallelogrammi.
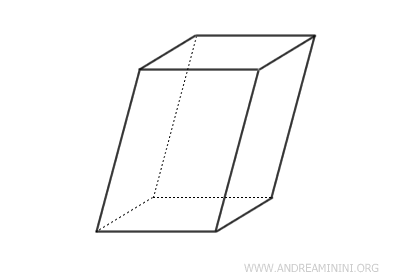
Si tratta di un solido a 6 facce, dove ciascuna faccia è un parallelogrammo, 12 spigoli e 8 vertici.
Un parallelepipedo ha le seguenti caratteristiche:
- Le facce opposte sono parallele e congruenti tra loro.
- Gli spigoli opposti sono paralleli e congruenti tra loro.
- I vertici opposti sono allineati su rette parallele.
Le lunghezze dei tre spigoli che escono da un vertice sono dette dimensioni del parallelepipedo.
La geometria del parallelepipedo è stata studiata fin dai tempi degli antichi greci, con matematici come Euclide che hanno scritto trattati sulle sue proprietà e caratteristiche.
Tipi di parallelepipedi
Esistono diversi tipologie di parallelepipedi in base alla natura delle sue facce.
- Parallelepipedi retti
Un parallelepipedo retto ha dei rettangoli nelle facce laterali.
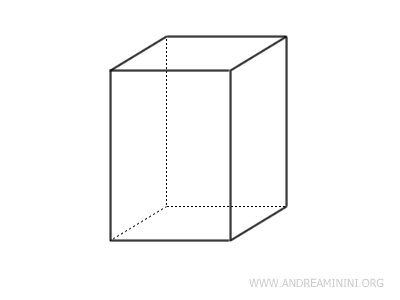
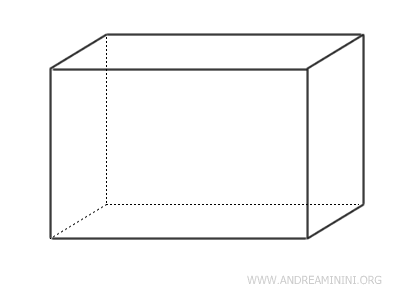
- Parallelepipedi rettangolari
Il parallelepipedo rettangolo è un parallelepipedo in cui le basi sono dei rettangoli. Di conseguenza, tutte le facce sono dei rettangoli.
- Parallelepipedi obliqui
In un parallelepipedo obliquo le facce laterali non sono dei rettangoli. Almeno una delle facce è un rombo o un parallelogramma generico.

In particolar modo sono abbastanza comuni nella geometria solida i seguenti casi particolari di parallelepipedo:
- Romboedro
E' un parallelepipedo in cui le sei facce sono rombi congruenti.
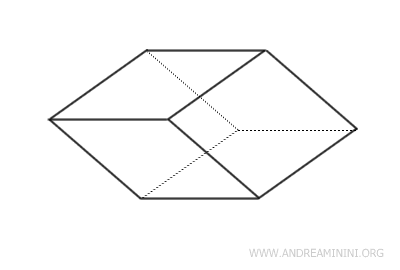
- Cubo
E' un parallelepipedo in cui le sei facce sono quadrati congruenti. Si tratta di un caso particolare sia di parallelepipedo rettangolo che di romboedro.
Le formule del parallelepipedo
Come in ogni prisma il volume V di un parallelepipedo è dato dal prodotto dell'area di una delle sue basi AB per l'altezza h.
$$ V = A_B \cdot h $$
Questo accade perché il parallelepipedo è una forma particolare di prisma.
Parallelepipedo rettangolo
Nel caso di un parallelepipedo rettangolare, dove le dimensioni delle basi sono l (lunghezza), w (larghezza) e h (altezza).
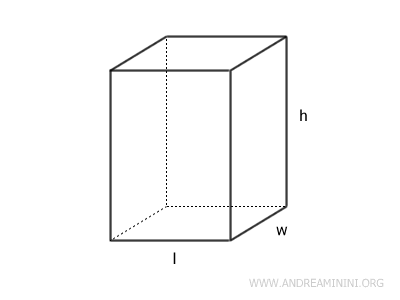
Il volume V è uguale al prodotto delle tre dimensioni:
$$ V = l \cdot w \cdot h $$
Dove il prodotto AB=l·w è l'area di una base.
$$ V = A_B \cdot h $$
La superficie laterale SL del parallelepipedo rettangolo è uguale al perimetro della base 2(w+l) per l'altezza (h).
$$ S_L =2 \cdot (w + l ) \cdot h $$
Dove PB=2(w+l) è il perimetro di una base.
$$ S_L =P_B \cdot h $$
In alternativa, la superficie laterale si può calcolare anche come somma delle aree delle facce laterali
$$ S_L = 2 \cdot (w \cdot h + l \cdot h ) $$
La superficie totale ST di un parallelepipedo è la somma delle aree di tutte le sue sei facce. E' uguale alla superficie laterale SL=2(w+l)h più due volte l'area del poligono della base 2lw:
$$ S_T = S_L + 2 S_B $$
$$ S_T = 2(w+l)h + 2lw $$
$$ S_T = 2lw + 2lh + 2wh $$
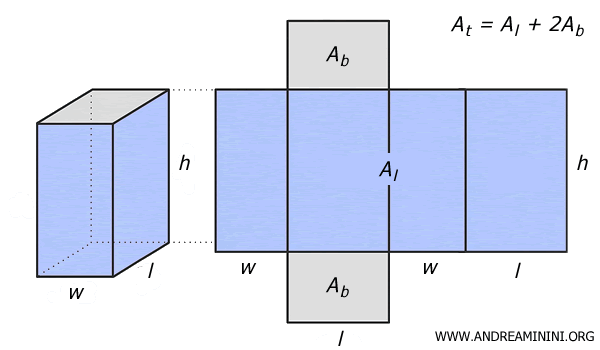
Nota. Basta ricordarsi che la superficie totale o area totale $ A_t $ è uguale alla somma tra l'area laterale $ A_l $ più due volte l'area di base $ A_l $. Guardando lo sviluppo del parallepipedo rettangolo il senso della formula diventa più evidente.
La diagonale (d) del parallelepipedo rettangolo è uguale alla radice quadrata della somma dei quadrati di ciascuna dimensione
$$ d = \sqrt{l^2+w^2+h^2} $$
Il parallelepipedo rettangolo
Un parallelepipedo rettangolo è un solido in cui le basi e le facce laterali sono rettangoli.
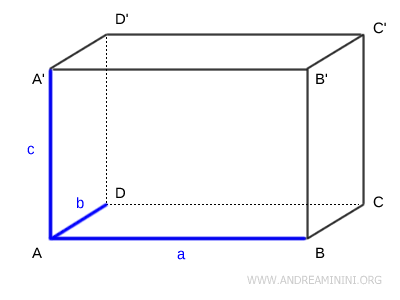
Le dimensioni del parallelepipedo sono le lunghezze dei tre spigoli uscenti da uno stesso vertice: \( a, b, c \).
Nota. Il concetto delle dimensioni di un parallelepipedo è più intuitivo e comunemente usato nel caso di un parallelepipedo rettangolo, dove gli spigoli sono perpendicolari tra loro e la geometria è più semplice e facilmente misurabile. Ad esempio, per misurare la lunghezza delle diagonali si può usare il teorema di Pitagora. In un parallelepipedo generico, invece, le dimensioni esistono ancora ma i calcoli per lunghezze e diagonali diventano più complessi perché i lati non sono necessariamente perpendicolari tra loro. In questo caso vanno considerati anche gli angoli tra gli spigoli.
La diagonale del parallelepipedo \( d \) è il segmento che unisce due vertici opposti.
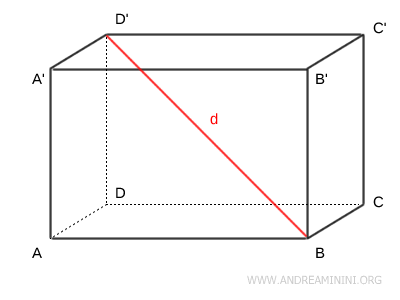
In un parallelepipedo rettangolo le diagonali sono congruenti tra loro.
La formula per misurare la lunghezza della diagonale dipende da tutte e tre le dimensioni del solido.
\[ d = \sqrt{a^2 + b^2 + c^2} \]
Questa formula posso utilizzarla per calcolare la distanza massima tra due vertici opposti.
Dimostrazione. Per dimostrare questa formula considero la diagonale $ d $ del parallelepipedo e la diagonale della base $ d_b $ del rettangolo ABCD.
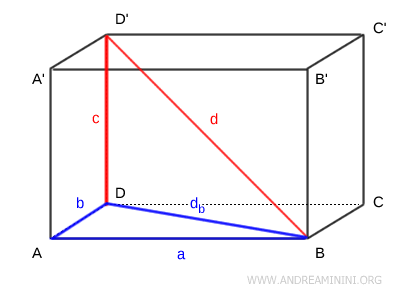
Applico il teorema di Pitagora al triangolo rettangolo $ ABD $ formato dai lati della base e ottengo la lunghezza della diagonale $ d_b $ del rettangolo. \[ d_b^2 = a^2 + b^2 \] \[ d_b = \sqrt{a^2 + b^2} \] Ora applico il teorema di Pitagora al triangolo rettangolo rettangolo $ DBD' $ che ha come cateti la diagonale della base \( d_b \) e l'altezza \( c \) \[ d^2 = d_b^2 + c^2 \] Sapendo che \( d_b^2 = a^2 + b^2 \) \[ d^2 = (a^2 + b^2) + c^2 \] \[ \sqrt{d^2} = \sqrt{a^2 + b^2 + c^2} \] \[ d = \sqrt{a^2 + b^2 + c^2} \] Quindi, la lunghezza della diagonale del parallelepipedo rettangolo è data dalla formula: \[ d = \sqrt{a^2 + b^2 + c^2} \] .
Osservazioni e note
Alcune osservazioni e note a margine sui parallelepipedi.
- Le facce opposte di un parallelepipedo sono congruenti e parallele
Le superfici opposte di un parallelepipedo, cioè quelle che non hanno vertici in comune, sono sia congruenti che parallele tra loro.
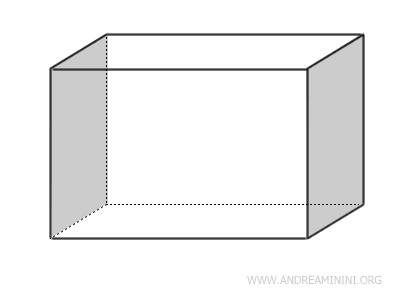
- Le diagonali del parallelepipedo passano tutte per uno stesso punto nel quale si bisecano in due segmenti congruenti.
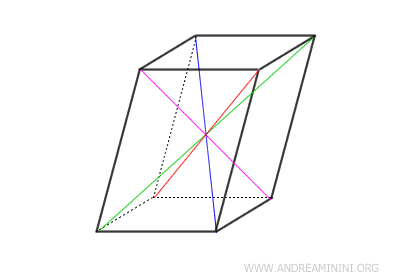
Dimostrazione. In questo parallelepipedo la figura $ ABC'D' $ è un parallelogramma perché ha i lati opposti congruenti e paralleli, quindi le sue diagonali $ AC' $ e $ BD' $ si incontrano nel loro punto medio $ O $. Quindi $ OA \cong OC' \cong OB \cong OD' $.
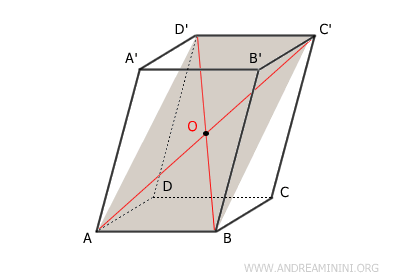
Anche la figura $ BCD'A' $ è un parallelogramma perché ha i lati opposti congruenti e paralleli. Quindi le diagonali $ BD' $ e $ A'C' $ si incontrano nel loro punto medio $ O $ dove si bisecano $ OB \cong OC \cong OA' \cong OD' $. Il punto $ O $ è lo stesso del caso precedente $ ABC'D' $ perché il segmento $ BD' $ è in comune.
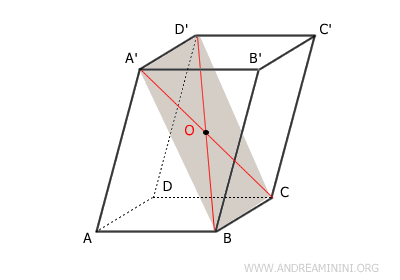
Lo stesso discorso può essere ripetuto con le altre diagonali del parallelepipedo ottenendo lo stesso risultato. Tutte le diagonali si bisecano in due segmenti congruenti nello stesso punto O. - In un parallelepipedo rettangolo le diagonali sono tutte congruenti fra loro.
- Se due parallelepipedi rettangoli hanno basi congruenti $ A_B $, allora i loro volumi sono proporzionali alle rispettive altezze. $$ \frac{V_1}{V_2} = \frac{A_B \cdot h_1}{A_B \cdot h_2} = \frac{h_1}{h_2} $$
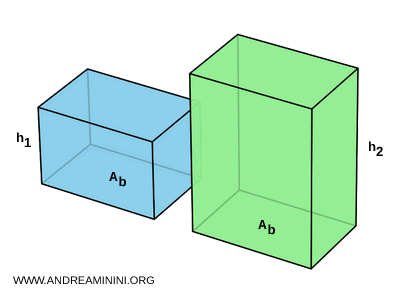
Dimostrazione. Il volume $ V $ di un parallelepipedo rettangolo si calcola come prodotto delle tre dimensioni: $$ V = l \cdot w \cdot h $$ dove il prodotto $A_B = l \cdot w $ rappresenta l’area della base. Quindi: $$ V = A_B \cdot h $$ Se due parallelepipedi hanno basi congruenti, cioè con la stessa area $ A_B $, e volumi uguali, allora devono avere anche la stessa altezza: $$ V_1 = V_2 \quad \text{e} \quad A_{B_1} = A_{B_2} \quad \Rightarrow \quad h_1 = h_2 $$ Viceversa, se i due parallelepipedi hanno basi congruenti ma volumi diversi, allora i volumi saranno proporzionali alle relative altezze: $$ \frac{V_1}{V_2} = \frac{A_B \cdot h_1}{A_B \cdot h_2} = \frac{h_1}{h_2} $$ Pertanto, il volume è proporzionale all’altezza, a parità di base.
E così via.
