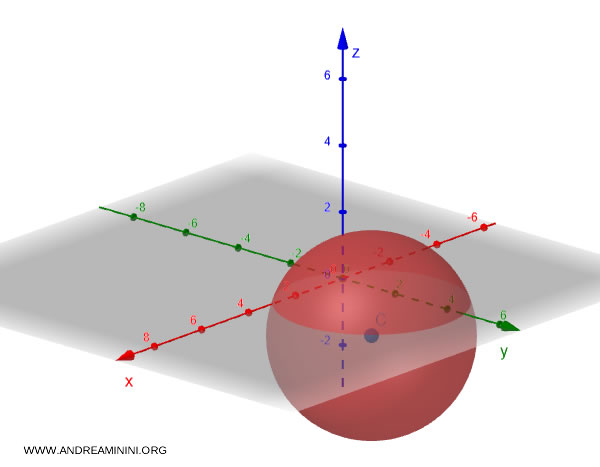
Sfera
La sfera un solido ottenuto dalla rotazione completa di un semicerchio attorno al suo diametro. E' una figura geometrica perfettamente simmetrica.
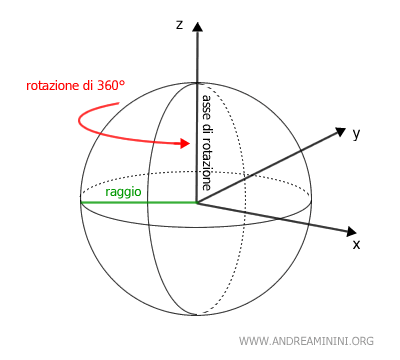
La rotazione di 360° della semicirconferenza traccia la superficie sferica.
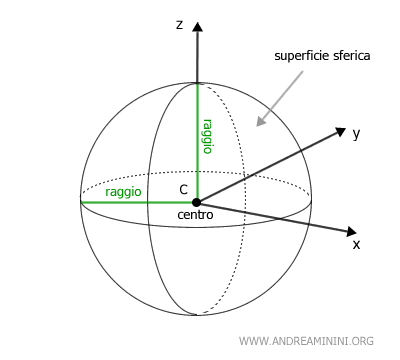
Il punto C è il centro della sfera ed è equidistante da ogni punto della superficie sferica.
Il raggio della semicirconferenza determina il raggio della sfera ossia il segmento che congiunge il centro della sfera con i punti della superficie sferica.
Allo stesso modo, posso considerare la sfera come un solido di rotazione ottenuto tramite la rotazione di 180° di un cerchio. Il risultato finale è lo stesso.
La sfera può essere definita anche come l'insieme di tutti i punti nello spazio (luogo geometrico) che si trovano a una distanza minore o uguale da un punto comune chiamato centro (C).
La superficie sferica, invece, è il luogo geometrico dei punti che hanno la distanza dal centro uguale al raggio della sfera.
I primi a studi della sfera risalgono all'antichità. Matematici greci come Platone e Archimede furono i primi a studiare le proprietà della sfera. In particolar modo, Archimede scoprì formule fondamentali per calcolare il volume e l'area superficiale delle sfere. La sfera ha avuto un ruolo significativo anche nella filosofia e nella cosmologia. Per i filosofi greci, la sfera rappresentava la perfezione, l'armonia e l'universo. Questo simbolismo si trova anche in alltre culture, dove la sfera è spesso associata ai concetti di completezza e infinito.
Le formule
Le principali formule per calcolare le metriche di una sfera:
- Superficie sferica
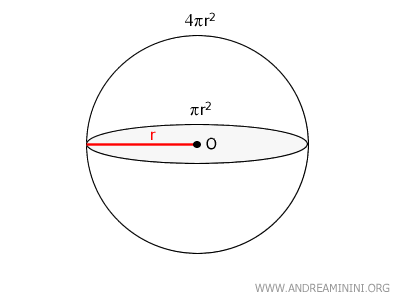
L'area superficiale di una sfera è data dalla formula $$ 4πr^2 $$ dove r è il raggio della sfera.Nota. L'area della sfera è quattro volte l'area del cerchio massimo. $$ 4 \cdot \pi r^2 $$
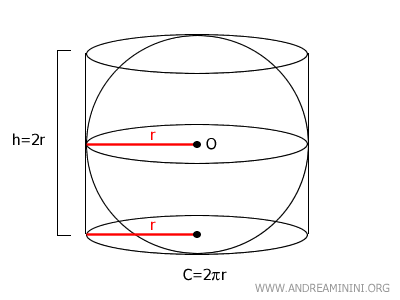
Si può anche dimostrare che l'area della sfera è equivalente alla superficie laterale $ A_L $ del cilindro circoscritto alla sfera. $$ A_L = C \cdot h = 2 \pi r \cdot 2r = 4 \pi r^2 $$
- Volume
Il volume di una sfera è proporzionale al cubo del suo raggio ed è dato dalla formula seguente: $$ \frac{4}{3}πr^3$$
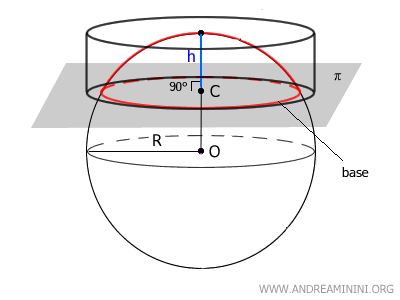
Le calotte della sfera
Una calotta sferica è una parte della superficie di una sfera compresa tra un piano secante e la sfera stessa.
Quando un piano (π) interseca una sfera, divide la sua superficie in due parti: ciascuna di queste prende il nome di calotta o calotta sferica.
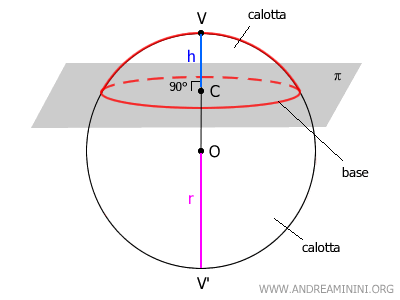
Ogni calotta è caratterizzata da tre elementi fondamentali:
- La base: è la circonferenza che ottengo tramite 'intersezione tra il piano e la sfera. E' un cerchio con centro nel punto C.
- Il vertice (V): è il punto della sfera più distante dal piano, allineato con il centro della base lungo il diametro della sfera.
- L’altezza (h): è la distanza tra il vertice (V) della calotta e il centro (C) della base. Questa altezza è sempre perpendicolare al piano della base.
Il diametro VV' della sfera che passa per il centro (C) della base è anche l’asse di simmetria della calotta. Questo asse attraversa la calotta verticalmente e la divide in due parti uguali.
Alcuni casi particolari
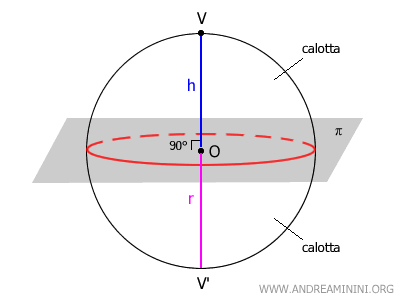
Se il piano (π) passa esattamente per il centro (O) della sfera, le due calotte risultanti sono emisferi congruenti.
In questo caso particolare, ogni calotta non è più una semplice porzione curva, ma esattamente la metà della superficie della sfera.
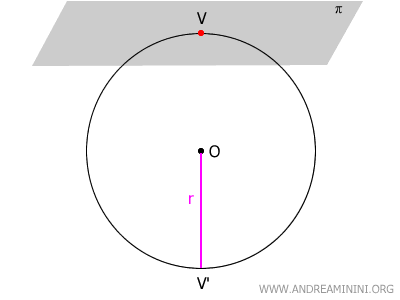
Se invece il piano (π) è tangente alla sfera, la calotta scompare e resta solo un punto V sulla superficie della sfera.
Nota. La calotta sferica ha diverse proprietà geometriche. Ad esempio, mantiene la simmetria e la curvatura originale della sfera, con un vertice e una base ben definiti.
L'area della calotta sferica
L'area della calotta sferica si calcola tramite la formula
$$ A= 2 \pi R h $$
Dove $ R $ è il raggio della sfera e $ h $ è l'altezza della calotta.
Esempio
Immagino una sfera con raggio \( R = 5\,cm \). Se taglio la sfera esattamente a metà, ottengo una calotta con $ h = R = 5\,cm $.
Applicando la formula ottengo la superficie della calotta
\[ A = 2 \pi R h = 2 \pi \cdot 5 \cdot 5 = 50 \pi \approx 157.08\,cm^2 \]
E' esattamente l’area della metà della superficie sferica.
Dimostrazione. L’area della superficie sferica è: \[ A_{\text{totale}} = 4 \pi R^2 \] Questa formula rappresenta l’intera superficie di una sfera di raggio \( R \). Se divido la sfera a metà con un piano passante per il centro, ottengo un emisfero, la cui superficie è esattamente la metà: \[ A_{\text{emisfero}} = 2 \pi R^2 \] Ora osservo un caso particolare: una calotta sferica la cui altezza \( h \) è esattamente uguale al raggio \( R \) della sfera. In altre parole, la calotta coincide con l’intero emisfero. Sostituendo nella formula generica della calotta o della zona: \[ S = 2 \pi R h \] e ponendo \( h = R \), ottengo: \[ S = 2 \pi R \cdot R = 2 \pi R^2 \] che corrisponde perfettamente all’area dell’emisfero trovata in precedenza. Questo conferma che la formula \( S = 2 \pi R h \) è corretta anche nei casi estremi, come quello di una calotta emisferica.
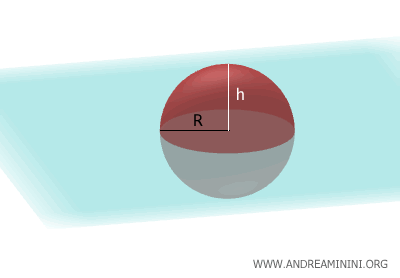
Di conseguenza, l’area della zona sferica è equivalente all’area della superficie laterale di un cilindro che abbia lo stesso raggio della sfera e un’altezza uguale a quella della calotta. Anche la superficie laterale di un cilindro è $ S_L = 2 \pi R h $
La zona sferica
La zona sferica è la parte di superficie sferica delimitata da due piani paralleli secanti.
I due piani intersecano la sfera in due circonferenze chiamate basi della zona, tagliando la superficie sferica in tre parti distinte.
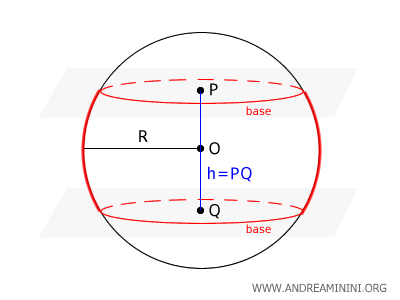
La parte compresa tra i due piani prende il nome di zona sferica. È una sorta di fascia curva, avvolgente, che si sviluppa tra due “tagli” circolari sulla sfera.
Nota. In altre parole, se immagino la sfera come il globo terrestre, è come tracciare due linee di latitudine distinte, la zona sferica è l'anello compreso tra di esse.
Il diametro della sfera che passa per il segmento $ PQ $ che unisce i centri $ P $ e $ Q $ delle due basi è detto asse di simmetria della zona, mentre la distanza tra i centri delle due basi prende il nome di altezza della zona e si indica con \( h \).
L'area della zona sferica
L’area \( S \) di una zona sferica si calcola con la stessa formula usata per una calotta sferica:
\[ S = 2 \pi R h \]
Dove \( R \) è il raggio della sfera e \( h \) è l’altezza della zona ossia la distanza tra i due piani che la delimitano.
Nota. Di fatto, la calotta sferica è un caso particolare di zona sferica, in cui uno dei due piani coincide con l’estremo della sfera, cioè taglia la sfera tangenzialmente. Per questa ragione la formula per il calcolo dell’area è esattamente la stessa, anche in questo caso l’area dipende solo dal raggio della sfera e dall’altezza della porzione curva.
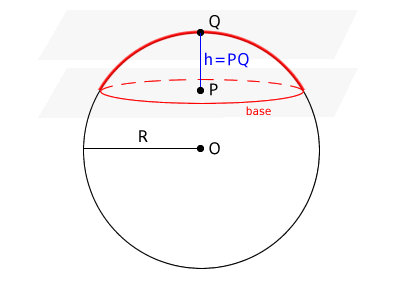
Esempio
Considerio una sfera con raggio \( R = 10\,cm \) e due piani paralleli che tagliano la sfera generando una zona sferica alta \( h = 4\,cm \).
L'area della zona sferica è circa \( 251.33\,cm^2 \)
$$ S = 2 \pi R h = 2 \pi \cdot 10 \cdot 4 = 80 \pi \approx 251.33\,cm^2 $$
Nota. L’area della zona sferica può essere assimilata all’area della superficie laterale di un cilindro che abbia lo stesso raggio della sfera e un’altezza uguale a quella della zona. Anche la superficie laterale di un cilindro è $ S_L = 2 \pi R h $
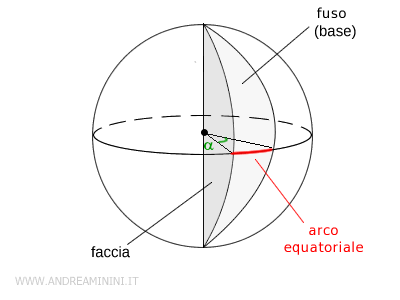
Il fuso sferico
Il fuso sferico è una porzione della superficie di una sfera delimitata da due semipiani che passano per il centro della sfera.
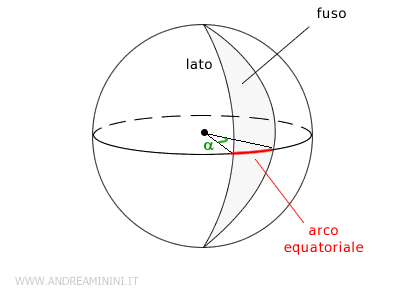
Gli elementi principali del fuso sferico sono:
- Diedro del fuso: è l'angolo solido (α) formato dai due semipiani.
- Arco equatoriale: è l’arco di circonferenza massima (simile all’equatore) contenuto nel fuso.
- Lati del fuso: sono le semicirconferenze individuate dai due semipiani sulla superficie della sfera.
In parole semplici, un fuso sferico assomiglia a una "fetta" di arancia, tagliata lungo i suoi spicchi.
La superficie del fuso sferico
L'area del fuso dipende dall'ampiezza del diedro. Posso calcolarla in due modi:
- Se l'angolo del diedro è espresso in radianti: \[ S_f = 2 \alpha_{\text{rad}} R^2 \]
- Se l'angolo del diedro è espresso in gradi: \[ S_f = \frac{\alpha^\circ}{90^\circ} \pi R^2 \]
Dove \( S_f \) è l'area del fuso, \( R \) è il raggio della sfera, \( \alpha_{\text{rad}} \) è l'ampiezza del diedro in radianti, \( \alpha^\circ \) è l'ampiezza del diedro in gradi.
L'importante è ricordare che l'area dipende direttamente dalla misura dell’angolo diedro (α), proporzionata all’intera superficie della sfera.
Dimostrazione. L'area totale della superficie di una sfera è: \[ A_{\text{totale}} = 4\pi R^2 \] Il fuso rappresenta una frazione di quest'area, proporzionale all'ampiezza del diedro. Quindi, in radianti: la proporzione è tra \( \alpha_{\text{rad}} \) e \( 2\pi \) (l’angolo completo). \[ A_{\text{fuso}} = 4\pi R^2 \cdot \frac{ \alpha_{\text{rad}} }{2 \pi} =2\alpha_{\text{rad}} R^2 \] In gradi: la proporzione è tra \( \alpha^\circ \) e \( 360^\circ \), \[ A_{\text{fuso}} = 4\pi R^2 \cdot \frac{ \alpha_{\text{rad}} }{360°} = \frac{\alpha^\circ}{90^\circ} \pi R^2 \]
Esempio
Devo calcolare l'area di un fuso sferico di una sfera di raggio \( R = 5 \, \text{cm} \), con diedro di \( 60^\circ \). Applico la formula:
\[ S_f = \frac{60^\circ}{90^\circ} \pi R^2 = \frac{2}{3} \pi (5)^2 \]
\[ S_f = \frac{2}{3} \pi \times 25 = \frac{50}{3} \pi \, \text{cm}^2 \]
L'area del fuso è circa \( 52,36 \, \text{cm}^2 \).
Esempio 2
Una sfera ha raggio \( 10 \, \text{cm} \). Un fuso ha un diedro di \( \frac{\pi}{4} \, \text{radianti} \). Ora calcolo l'area del fuso usando la formula in radianti:
\[ S_f = 2 \alpha_{\text{rad}} R^2 = 2 \times \frac{\pi}{4} \times 10^2 \]
\[ S_f = \frac{\pi}{2} \times 100 = 50\pi \, \text{cm}^2 \]
Pertanto, l'area del fuso è circa \( 157,08 \, \text{cm}^2 \).
Il segmento sferico
Un segmento sferico è una porzione di solido che si ottiene tagliando una sfera con uno o due piani paralleli.
A] Il segmento sferico a una base
Un segmento sferico a una base si ottiene tagliando la sfera con un solo piano ed eliminando la parte sopra o sotto il piano.
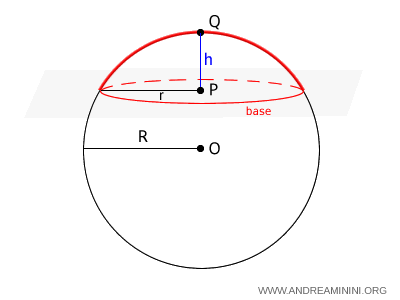
La superficie inferiore (o superiore) del segmento è una calotta sferica, detta anche "calotta emisferica", se il piano taglia a metà la sfera.
La base del segmento è un cerchio corrispondente alla sezione della sfera sul piano.
Formula del volume
Se il segmento sferico ha altezza $ h $ e la base ha raggio $ r $, il volume del segmento sferico è equivalente alla somma di una sfera di diametro congruente a $ h $ e di un cilindro con la stessa base del segmento e un'altezza $ h/2 $.
$$ V = \frac{4}{3} \pi ( \frac{h}{2} )^3 + \pi r^2 \cdot \frac{h}{2} $$
Questa formula è semplicemente la somma di due volumi, quello di una sfera e di un cilindro.
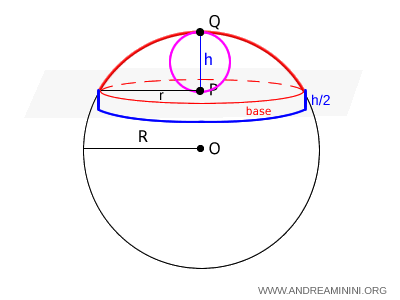
Può essere usata sia per calcolare il volume della parte superiore del segmento a una base, come nell'esempio precedente, sia quello della parte inferiore.
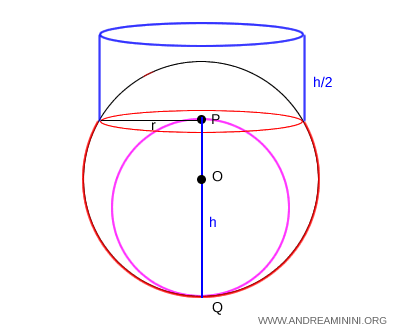
La forma compatta della formula del volume
La formula del volume può essere scritta anche nella forma semplificata
$$ V = \frac{1}{3} \pi h^2 (3R-h) $$
Dove $ R $ è il raggio della sfera.
Dimostrazione. Considero il segmento sferico a una base con altezza $ h =CV $ e raggio di base $ r=BC $
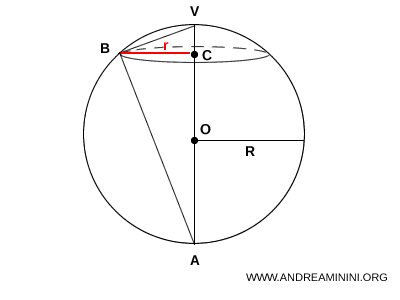
Applico il secondo teorema di Euclide al triangolo rettangolo VAB si ottiene la relazione $$ BC^2 = AC \cdot CV $$ Dove $ BC $ è il raggio $ r $ della base del segmento sferico. $$ r^2 = AC \cdot CV $$ Il segmento $ AC = 2R - h $ è la differenza tra il diametro della sfera e l'altezza del segmento sferico. $$ r^2 = (2R - h ) \cdot CB $$ Infine, $ CV $ è l'altezza $ h $ del segmento sferico. $$ r^2 = (2R - h ) \cdot h $$ $$ r^2 = 2Rh - h^2 $$ Sostituisco $ r^2 $ nella formula del volume del segmento sferico $$ V = \frac{4}{3} \pi ( \frac{h}{2} )^3 + \pi r^2 \cdot \frac{h}{2} $$ $$ V=\frac{4}{3}\,\pi\!\left(\frac{h}{2}\right)^{\!3}+ \pi \bigl(2Rh-h^{2}\bigr) \frac{h}{2} $$ $$ V=\frac{4}{3}\,\pi\!\left(\frac{h}{2}\right)^{\!3}+\pi R h^{2}-\frac{\pi h^{3}}{2} $$ Sviluppo il primo termine $$ V=\frac{4}{3}\,\pi\;\frac{h^{3}}{8} +\pi R h^{2}-\frac{\pi h^{3}}{2} $$ $$ \begin{aligned} V &=\frac{\pi h^{3}}{6}+\pi R h^{2}-\frac{\pi h^{3}}{2} \\[2pt] &=\pi R h^{2}\;+\;\left(\frac{1}{6}-\frac{1}{2}\right)\pi h^{3} \\[2pt] &=\pi R h^{2}-\frac{\pi h^{3}}{3} \end{aligned} $$ In forma fattorizzata diventa $$ \boxed{\;V=\frac{1}{3}\,\pi\,h^{2}\,(3R-h)\;} $$ che è la forma compatta del volume del segmento sferico a una base.
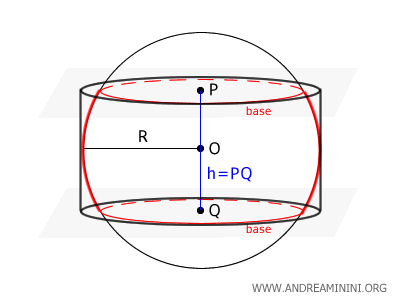
B] Il segmento sferico a due basi
Un segmento sferico a due basi è un pezzo di sfera compreso tra due piani paralleli che tagliano la sfera.
In altre parole, è un solido composto da una sfera tagliata da due piani orizzontali: la parte della sfera che rimane fra i due piani si chiama segmento sferico.
Il risultato finale è una sorta di cilindro curvo.
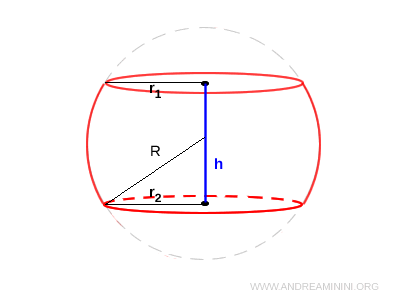
Gli elementi di cui è composto sono:
- La base superiore e la base inferiore sono due cerchi (le sezioni della sfera con i piani).
- La superficie laterale curva è la zona sferica.
- L'altezza del segmento sferico $ h $ è la distanza fra i due piani.
- Il raggio della sfera è il raggio della sfera da cui proviene il segmento.
Nota. Il segmento sferico non va confuso con la calotta sferica, che è il pezzo di sfera sopra (o sotto) un solo piano di taglio. Non è nemmeno il fuso sferico, un settore della superficie sferica delimitato da due semipiani che passano per il centro.
Formula del volume
Se il segmento sferico ha altezza $ h $ e le basi hanno raggi $ r_1 $ e $ r_2 $, e la sfera ha raggio $ R $, il volume è:
$$ V = \frac{πh}{6} (3r_1^2 + 3r_2^2 + h^2) $$
Nota. Il volume del segmento sferico a due basi è equivalente alla somma del volume di due cilindri, ciascuno di altezza pari a metà del segmento ($ h/2 $) e con basi congruenti a quelle del segmento, più il volume di una sfera di diametro uguale all'altezza del segmento.
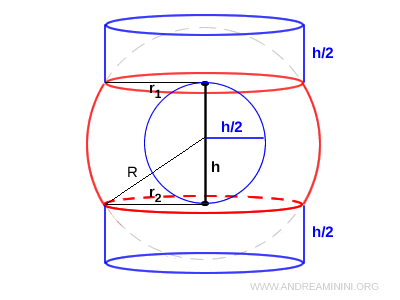
Ad esempio, i volumi dei due cilindri sono $$ V_1 = \pi r_1^2 \cdot \frac{h}{2} $$ $$ V_2 = \pi r_2^2 \cdot \frac{h}{2} $$ Il volume della sfera con diametro uguale a $ h $ e raggio $ h/2 $ è $$ V_3 = \frac{4}{3} \pi ( \frac{h}{2} )^3 $$ Sommo i tre volumi $$ V = V_1+ V_2+ V_3 $$ $$ V = \pi r_1^2 \cdot \frac{h}{2} + \pi r_2^2 \cdot \frac{h}{2}+ \frac{4}{3} \pi ( \frac{h}{2} )^3 $$ $$ V = \pi r_1^2 \cdot \frac{h}{2} + \pi r_2^2 \cdot \frac{h}{2}+ \frac{4}{3} \pi \frac{h^3}{8} $$ $$ V = \pi r_1^2 \cdot \frac{h}{2} + \pi r_2^2 \cdot \frac{h}{2}+ \frac{1}{6} \pi h^3 $$ $$ V = \frac{1}{6} \pi h \cdot ( 3r^2_1 + 3r^2_2 +h^2) $$ Il risultato finale è la formula del volume del segmento sferico.
Lo spicchio sferico
Lo spicchio sferico è la parte solida di una sfera compresa tra due semicerchi distinti, che corrispondono alle "facce" dello spicchio. La superficie curva che li congiunge è un fuso sferico, detto talvolta anche "base laterale".
La forma di questo solido è simile a uno spicchio di arancia.
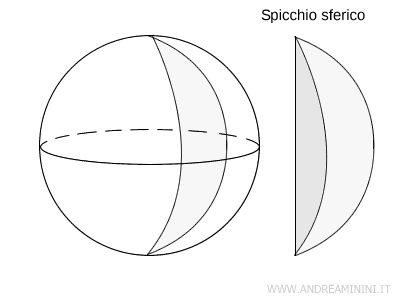
Il volume dello spicchio sferico è proporzionale all'angolo di apertura tra le due facce.
Se l’angolo è espresso in radianti:
$$V : \frac{4}{3} \pi R^3 = \alpha_{rad} : 2\pi$$
Da cui ottengo la formula del volume dello spicchio sferico:
$$V = \alpha_{rad} \cdot \frac{2}{3} R^3$$
Nota. Se l’angolo è espresso in gradi, la proporzione diventa: $$V : \frac{4}{3} \pi R^3 = \alpha : 360^\circ$$ La formula dl volume corrispondente è: $$V = \frac{\alpha}{360^\circ} \cdot \frac{4}{3} \pi R^3$$ ossia $$V = \frac{\alpha}{270^\circ} \pi R^3$$
L'anello sferico
L’anello sferico è un solido che nasce dalla sottrazione di un tronco di cono inscritto da un segmento sferico a due basi.
Si forma considerando un segmento sferico a due basi e un tronco di cono inscritto, i cui contorni coincidono con quelli del segmento sferico.
Le due sezioni circolari definiscono le basi del segmento.
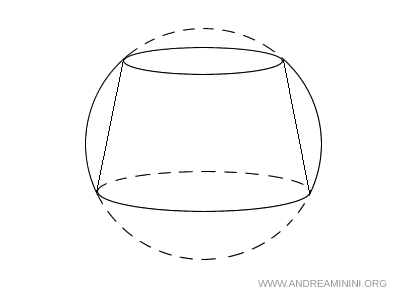
All’interno di questo segmento sferico si può inscrivere un tronco di cono, ovvero la parte di un cono compresa tra due piani paralleli alle sue basi.
Le basi del tronco coincidono con le basi circolari del segmento sferico.
La porzione di sfera compresa tra la superficie laterale del tronco di cono e la zona sferica compresa nel segmento sferico, costituisce l'anello sferico.
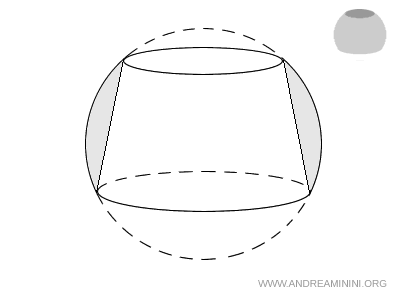
In altre parole, l’anello sferico è ciò che resta della zona sferica dopo aver “scavato” al suo interno la superficie del tronco di cono.
Il volume dell'anello sferico
Il volume dell'anello sferico è la differenza tra il volume del segmento sferico e quello del tronco di cono inscritto.
$$ V = \frac{1}{6} \pi a^2 h $$
Dove $ a $ è l'apotema del tronco di cono mentre $ h $ è l'altezza.
Dimostrazione. Parto dalla definizione del volume dell'anello sferico come differenza dei volumi del segmento sferico e del tronco di cono. $$ V_{\text{anello}} = V_{\text{segmento sferico}} - V_{\text{tronco di cono}} $$ Il volume del segmento sferico a due basi di altezza $h$, con raggi delle basi $r_1$ e $r_2$, è dato da: $$
V_{\text{segmento sferico}} = \frac{\pi h}{6} \left( 3r_1^2 + 3r_2^2 + h^2 \right)
$$ Il volume del tronco di cono di altezza $h$, con raggi di base $r_1$ e $r_2$, è:
$$ V_{\text{tronco di cono}} = \frac{1}{3} \pi h \left( r_1^2 + r_1 r_2 + r_2^2 \right) $$ Ora calcolo la differenza: $$ V_{\text{anello}} = V_{\text{segmento sferico}} - V_{\text{tronco di cono}} $$ $$ V_{\text{anello}} = \frac{\pi h}{6} \left( 3r_1^2 + 3r_2^2 + h^2 \right) - \frac{1}{3} \pi h \left( r_1^2 + r_1 r_2 + r_2^2 \right) $$ Metto tutto sotto il comune denominatore: $$ V_{\text{anello}} = \frac{\pi h}{6} \left[ (3r_1^2 + 3r_2^2 + h^2) - 2 ( r_1^2 + r_1 r_2 + r_2^2 ) \right]
$$ Sviluppo i termini all’interno della parentesi: $$ V_{\text{anello}} = \frac{\pi h}{6} \left[ 3r_1^2 + 3r_2^2 + h^2 - 2r_1^2 - 2r_1 r_2 - 2r_2^2 \right] $$ $$ V_{\text{anello}} = \frac{\pi h}{6} \left[ r_1^2 + r_2^2 + h^2 - 2 r_1 r_2 \right] $$ I termini seguenti formano il quadrato di un binomio $ r_1^2 + r_2^2 - 2r_1 r_2 = (r_1 - r_2)^2 $. Quindi la parentesi si semplifica in: $$ V_{\text{anello}} = \frac{\pi h}{6} \left[ (r_1 - r_2)^2 + h^2 \right] $$ Ora introduco l’apotema $a$ del tronco di cono. Geometricamente, si ha $ a^2 = (r_1 - r_2)^2 + h^2 $. In questo modo ottengo finalmente la forma compatta che volevo dimostrare: $$ V_{\text{anello}} = \frac{1}{6} \pi a^2 h $$ Dove $a$ è l'apotema del tronco di cono inscritto e $h$ è l'altezza del segmento sferico.
Il settore sferico
Un settore sferico è una porzione della sfera delimitata da un cono avente per vertice il centro della sfera e per base una calotta sferica.
In altre parole, un settore sferico è la parte di sfera che si ottiene facendo ruotare di 360° un settore circolare di un cerchio intorno a un diametro che non lo attraversa.
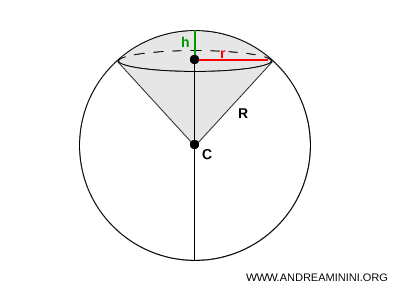
Lo si può considerare come un solido formato da un segmento sferico a una base e un cono retto con la stessa base e il vertice nel centro della sfera.
Tuttavia, questo è solo un caso particolare di settore sferico.
Il volume del settore sferico è
$$ V = \frac{2}{3} \pi R^2 h $$
Dove $ R $ è il raggio della sfera e $ h $ è l'altezza del segmento sferico.
L'area della superficie è invece
$$ A = \pi R(2 h+r) $$
Dove $ r $ è il raggio del settore circolare.
Dimostrazione. Partendo dalla scomposizione in segmento sferico e cono con vertice nel centro della sfera, e usando la relazione fra i parametri geometrici, si arriva esattamente alla formula classica del volume del settore sferico. Il volume del segmento sferico è $$ V_{\text{seg}}=\frac{1}{3}\,\pi\,h^{2}\,(3R-h) $$ Il volume di un cono con vertice nel centro della sfera è $$ V_{\text{cono}}=\frac{1}{3}\,\pi\,r^{2}\,(R-h) $$ Dal triangolo rettangolo che si forma tagliando la sfera con il piano di base si ottiene una relazione tra $r$, $h$ e $R$ $$ r^{2}=R^{2}-(R-h)^{2}=2Rh-h^{2} $$ Per una spiegazione dettagliata su quest'ultimo passaggio, rimando alla dimostrazione che ho già fatto per ottenere la formula compatta del volume di un segmento sferico. Il volume del settore sferico può essere ottenuto sommando il volume del segmento sferico e del cono $$ \begin{aligned} V_{\text{settore}} &=V_{\text{seg}}+V_{\text{cono}} \\[2pt] &=\frac{1}{3}\,\pi\Bigl[h^{2}(3R-h)+r^{2}(R-h)\Bigr]. \end{aligned} $$ Sostituisco $ r^2 = 2Rh-h^{2} $ $$ \begin{aligned} h^{2}(3R-h)&+(2Rh-h^{2})(R-h) \\[2pt] &=\;3Rh^{2}-h^{3} \;+\; 2R^{2}h-3Rh^{2}+h^{3} \\[2pt] &=2R^{2}h \end{aligned} $$ Quindi, la forma del settore sferico è $$ \boxed{\,V_{\text{settore}}=\frac{1}{3}\,\pi\,(2R^{2}h)=\frac{2}{3}\,\pi\,R^{2}h\,} $$ In poche parole, la combinazione di “segmento sferico + cono” porta dunque, alla formula classica del volume del settore sferico.
Queste formule valgono solo per un settore sferico classico, ovvero la porzione di sfera delimitata da un cono retto avente il vertice nel centro della sfera.
In casi più complessi (settori obliqui, gusci sferici, combinazioni di solidi), per ottenere il volume è necessario analizzare la geometria specifica del settore sferico.
Altri casi di settori sferici
A seconda dei casi il volume di un settore sferico posso ottenerlo come somma o differenza del volume di altri solidi.
Ad esempio, in questo caso il volume del settore sferico è la differenza tra il volume di un segmento sferico e il volume di due coni.
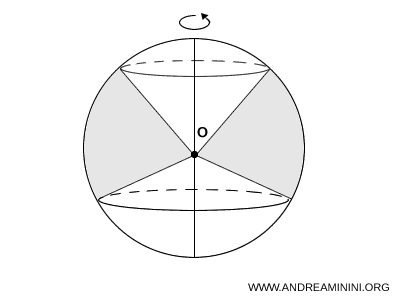
In quest'altro caso, invece, il volume del settore sferico si ottiene tramite la differenza di altri due settori sferici.
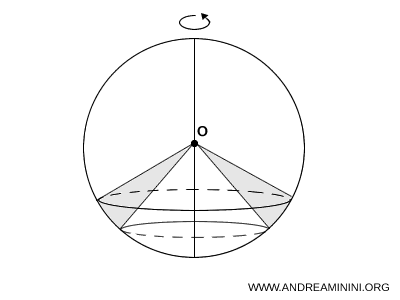
Quindi, la formula del volume va considerata caso per caso.
La sfera nella geometria analitica
In geometria analitica, la sfera è rappresentata da un'equazione che definisce tutti i punti nello spazio che hanno una distanza costante da un punto fisso, il centro.
L'equazione standard di una sfera con centro nel punto (x0,y0,z0) e raggio r è la seguente:
$$ (x−x_0)^2+(y−y_0)^2+(z−z_0)^2=r^2 $$
Dove (x,y,z) sono le coordinate di un punto qualsiasi dello spazio.
Sviluppando i calcoli si ottiene l'equazione della superficie sferica.
$$ x^2 + y^2 + z^2 + ax+by+cz + d = 0 $$
Dove $ a=-2x_0 $, $ b = -2y_0 $, $ c = - 2z_0 $, $ d = x_0^2 + y_0^2 + z_0^2 - r^2 $.
Questa equazione è una generalizzazione dell'equazione del cerchio nel piano cartesiano, estesa alla terza dimensione.
Quindi, le coordinate del centro $ (x_0, y_0, z_0) $ della sfera sono:
$$ x_0 = - \frac{a}{2} $$
$$ y_0 = - \frac{b}{2} $$
$$ z_0 = - \frac{c}{2} $$
Pertanto, il centro della sfera si trova alle coordinate
$$ c = (x_0, y_0, z_0 ) = \left( - \frac{a}{2} , - \frac{b}{2} , - \frac{c}{2} \right) $$
Se la sfera è centrata nell'origine O(0,0,0) del piano l'equazione si riduce a
$$ x^2 + y^2 +z^2 = r^2 $$
Il raggio della sfera è, invece, determinato dall'equazione:
$$ r = \sqrt{x_0^2 + y_0^2 + z_0^2 - d} $$
Spiegazione. Sapendo che il coefficiente $ d $ è: $$ d = x_0^2 + y_0^2 + z_0^2 - r^2 $$ Ricavo il raggio $ r $ $$ r^2 = x_0^2 + y_0^2 + z_0^2 - d $$ Calcolo la radice quadrati in entrambi i membri dell'equazione $$ \sqrt{ r^2 } = \sqrt{ x_0^2 + y_0^2 + z_0^2 - d } $$$$ r = \sqrt{ x_0^2 + y_0^2 + z_0^2 - d } $$
Ecco un esempio pratico di sfera costruita al centro del piano cartesiano con un raggio unitario.
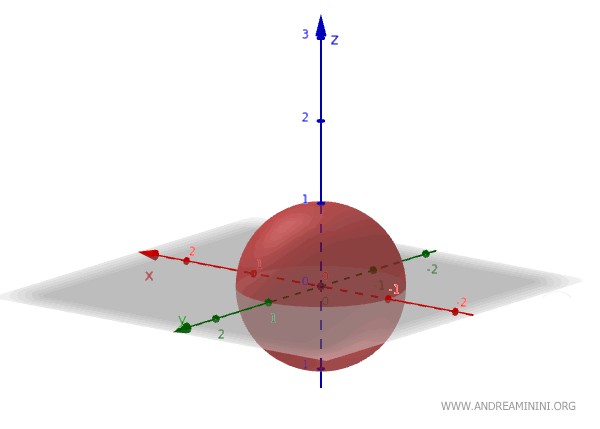
La condizione di realtà della sfera. Sapendo che $ d = a_0^2 + y_0^2 + z_0^2 - r^2 $ ottengo l'equazione del quadrato del raggio $$ r^2 = a_0^2 + y_0^2 + z_0^2 - d $$ Sostituisco le coordinate della sfera $ x_0 = - \frac{a}{2} $, $ y_0 = - \frac{b}{2} $, $ z_0 = - \frac{c}{2} $ $$ r^2 = ( - \frac{a}{2} )^2 + ( - \frac{b}{2} )^2 + ( - \frac{c}{2} )^2 - d $$$$ r^2 = \frac{a^2}{4} + \frac{b^2}{4} + \frac{c^2}{4} - d $$ Poiché il raggio è una lunghezza, quindi è sempre positivo, deduco che l'equazione $ x^2 + y^2 + z^2 + ax+by+cz + d = 0 $ descrive una sfera solo se i coefficienti soddisfano questa condizione $$ \frac{a^2}{4} + \frac{b^2}{4} + \frac{c^2}{4} - d \ge 0 $$
Esempio
Considero una sfera con il centro nel punto $ C: (1, 2, -1) $ e raggio $ 3 $.
L'equazione della superficie sferica è:
$$ (x−x_0)^2+(y−y_0)^2+(z−z_0)^2=r^2 $$
In questo caso le coordinate del centro sono $ x_0 = 1 $, $ y_0=2 $, $z_0 =-1 $ e il raggio è $ r=3 $
$$ (x−1)^2+(y−2)^2+(z−(-1))^2=r^2 $$
$$ (x−1)^2+(y−2)^2+(z+1)^2=3^2 $$
Sviluppo i quadrati.
$$ (x^2-2x+1) + (y^2-4y+4) + (z^2+2z+1)=9 $$
Porto tutti i termini al primo membro e sommo i termini simili.
$$ x^2 + y^2+z^2-2x-4y+2z+1+4+1- 9 = 0 $$
$$ x^2 + y^2+z^2-2x-4y+2z- 3 = 0 $$
Ho così ottenuto l'equazione della superficie sferica.
Verifica della condizione di realtà. In questo caso i coefficienti sono $ a=-2 $, $ b = -4 $, $c=2 $, $d = -3 $. Li sostituisco nella condizione di realtà della sfera per verificare se l’equazione descrive effettivamente una superficie sferica reale: $$ \frac{a^2}{4} + \frac{b^2}{4} + \frac{c^2}{4} - d \ge 0 $$$$ \frac{(-2)^2}{4} + \frac{(-4)^2}{4} + \frac{2^2}{4} - (-3) \ge 0 $$$$ \frac{4}{4} + \frac{16}{4} + \frac{4}{4} +3 \ge 0 $$$$ 1 + 4 + 1 +3 \ge 0 $$$$ 9 \ge 0 $$ La condizione di realtà è soddisfatta, quindi l'equazione $ x^2 + y^2+z^2-2x-4y+2z- 3 = 0 $ descrive effettivamente una superficie sferica reale.
Dimostrazione
Una superficie sferica è composta da punti che hanno la distanza dal centro $ (x_0,y_0, z_0) $ della sfera pari a quella del raggio $ r $ della sfera.
$$ \sqrt{(x-x_0)^2+ (y-y_0)^2 + (z-z_0)^2} = r $$
Elevo al quadrato entrambi i membri dell'equazione
$$ ( \sqrt{(x-x_0)^2+ (y-y_0)^2 + (z-z_0)^2} )^2 = r^2 $$
$$ (x-x_0)^2+ (y-y_0)^2 + (z-z_0)^2 = r^2 $$
Ora espando i quadrati
$$ x^2-2xx_0 +x_0^2 + y^2-2yy_0 +y_0^2 + z^2-2zz_0 +z_0^2 = r^2 $$
Assegno i coefficienti $ a=-2x_0 $, $ b = -2y_0 $, $ c = - 2z_0 $
$$ x^2+ax +x_0^2 + y^2+by +y_0^2 + z^2+cz +z_0^2 = r^2 $$
$$ x^2 + y^2+ z^2 +ax +by +cz +x_0^2 +y_0^2 +z_0^2 - r^2 = 0 $$
Infine, raggruppo l'espressione $ d = x_0^2 + y_0^2 + z_0^2 - r^2 $.
$$ x^2 + y^2+ z^2 +ax +by +cz +d = 0 $$
Il risultato è l'equazione della superficie sferica.
L'equazione della sfera con le coordinate polari
L'equazione della sfera può essere espressa anche tramite le coordinate polari
$$ \begin{cases} x = x_0 + r \sin \theta \cos \theta \\ \\ y = y_0 + r \sin \theta \sin \theta \\ \\ z = z_0 + r \cos \theta \end{cases} $$
Osservazioni
Alcune osservazioni a margine sulla sfera
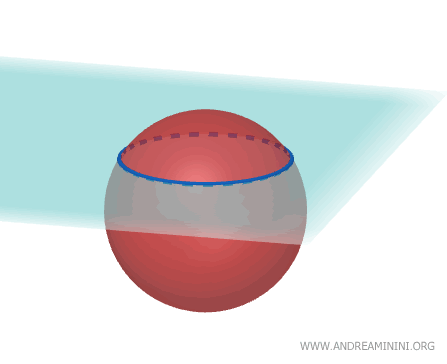
- Sezioni
Qualsiasi intersezione tra un piano e una sfera è un cerchio. Se il piano passa per il centro, la circonferenza è massima.
- Corda
Una corda della sfera è un segmento che congiunge due punti qualsiasi distinti sulla superficie della sfera. - Diametro
Il diametro della sfera è il doppio del raggio. Consiste in una corda passante per il centro della sfera. $$ d = 2r $$ - Piano esterno, tangente e secante di una sfera
Un piano α rispetto a una sfera Σ di centro C e raggio r è detto- esterno se la distanza tra il piano α e la sfera Σ è maggiore del raggio r. Il piano e la sfera non hanno punti in comune
- tangente se la distanza tra il piano α e la sfera Σ è uguale al raggio r.
- secante se la distanza tra il piano α e la sfera Σ è minore del raggio r.
- Iperper-sfera (o n-sfera)
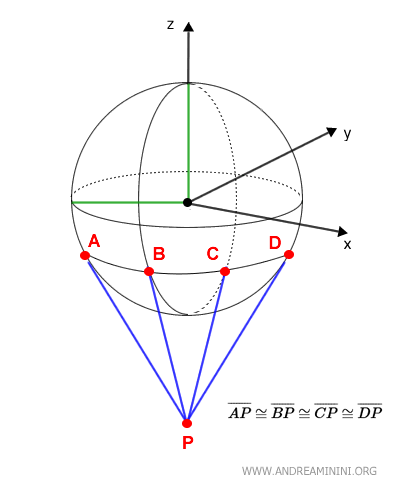
Generalizzazione della sfera a dimensioni superiori. Una 4-sfera è l'analogo quattro-dimensionale della sfera ordinaria. - Teorema dei segmenti tangenti a una sfera da un punto esterno
I segmenti tangenti a una sfera condotti da un punto P esterno alla sfera sono tra loro congruenti $ \overline{AP} \cong \overline{BP} \cong \overline{CP} \cong \overline{DP} $ Tutti i segmenti tangenti alla sfera condotti dallo stesso punto P formano un cono su base circolare.
E così via.
