Prisma

Un prisma è un poliedro caratterizzato da due facce parallele e congruenti, denominate basi, mentre le sue facce laterali sono tutte parallelogrammi.

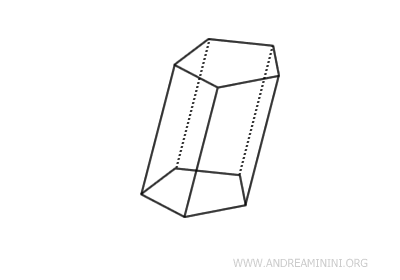
Il prisma è una figura solida fondamentale della geometria dello spazio.

Le caratteristiche del prisma

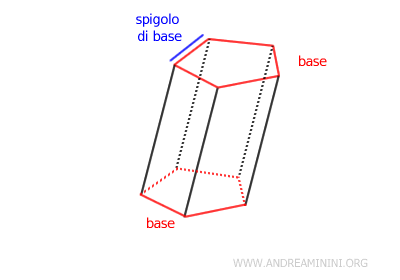
Le facce parallele e congruenti sono dette basi del prisma. Possono avere qualsiasi forma.

Ogni spigolo delle basi è detto spigolo di base.

La forma delle basi dà il nome al prisma. Ad esempio, un prisma con basi triangolari è chiamato prisma triangolare. Quello con basi a quattro angoli è detto prisma quadrangolare, a cinque angoli pentagonale, a sei angoli esagonale ecc. Se il poligono che definisce le basi è un poligono regolare, il prisma è detto prisma regolare. Viceversa, è detto "non regolare".

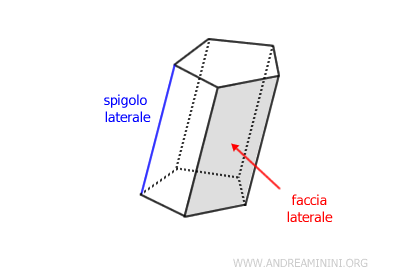
Le altre facce laterali sono dette facce laterali e sono parallelogrammi che congiungono i corrispondenti vertici delle basi.

Il segmento che congiunge due vertici non appartenenti alla stessa base è detto spigolo laterale.

In un prisma gli spigoli laterali sono tutti congruenti tra loro.

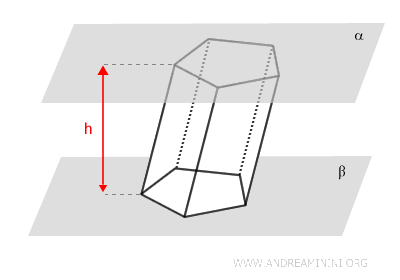
La distanza tra le due basi definisce l'altezza del prisma.

Le diagonali del prima sono i segmenti che congiungono due vertici che non appartengono alla stessa base.

Tipi di prismi

I prismi possono essere classificati in base alla forma delle loro basi:

• Prisma triangolare
  Ha basi a forma di triangolo.
• Prisma quadrangolare
  Ha basi a forma di quadrilatero.
• Prisma pentagonale
  Ha basi a forma di pentagono.
  
• Parallelepipedo
  Un parallelepipedo è un prisma le cui basi sono parallelogrammi.
  

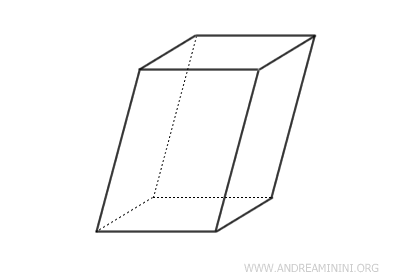
E così via, per ogni altro tipo di poligono.

Inoltre, i prismi possono essere classificati in base alla loro inclinazione:

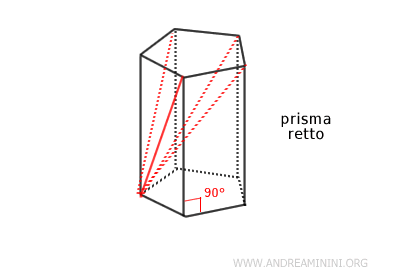
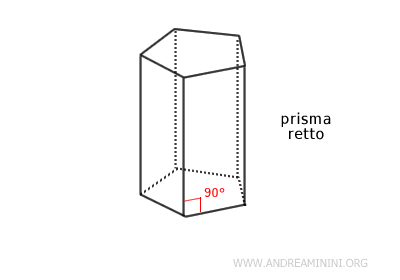
• Prisma retto
  Le facce laterali sono rettangoli e l'angolo tra la base e le facce laterali è di 90 gradi. Quindi, in un prisma retto gli spigoli laterali coincidono con l'altezza e sono perpendicolari ai piani delle basi.
  
• Prisma obliquo
  Le facce laterali sono parallelogrammi, ma non rettangoli.
  
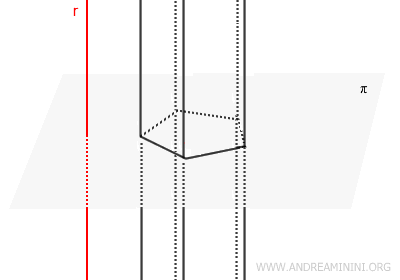
• Prisma indefinito
  Un prisma indefinito è una figura geometrica generata da un poligono e da un fascio di rette parallele a una retta \( r \) data, non appartenente al piano del poligono. Si estende indefinitamente in entrambe le direzioni lungo le rette parallele, formando una struttura tridimensionale infinita.
  
• Prisma definito
  Un prisma definito, o semplicemente prisma, è un poliedro ottenuto sezionando un prisma indefinito con due piani paralleli che lo intersecano. Ha due basi poligonali congruenti e dei parallelogrammi nelle facce laterali.
  

Il volume e la superficie di un prisma

Il volume di un prisma è dato dal prodotto dell'area della base A per l'altezza h del prisma: $$ V = A \cdot h $$

La superficie totale S di un prisma è la somma delle aree delle due basi e delle aree delle facce laterali.

Se P è il perimetro della base e h è l'altezza del prisma, l'area delle facce laterali è P h. Pertanto, la superficie totale è:

$$ S = 2A + P \cdot h $$

Il prisma retto

Un prima retto è un tipo di prisma in cui gli spigoli laterali sono perpendicolari al piano delle basi.

In un prisma retto le facce laterali sono dei rettangoli e l'altezza del prisma coincide con la lunghezza degli spigoli laterali.

Note

Alcune note aggiuntive, teoremi e osservazioni personali sul prisma.

• Teorema dell'equivalenza tra prismi
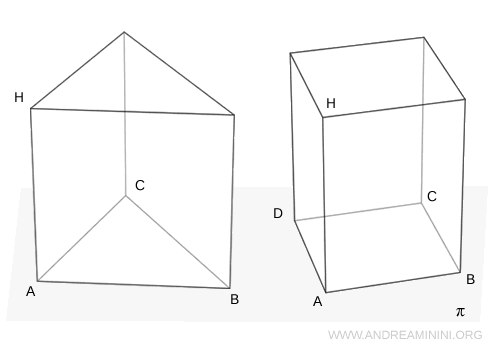
  Due prismi sono equivalenti in volume se hanno basi equivalenti (cioè con la stessa area) e altezze congruenti.

  Dimostrazione. Considero due prismi non necessariamente congruenti che poggiano su un medesimo piano $ \pi $. Per ipotesi iniziale, i due solidi hanno le basi di area uguale $ \text{Area}(ABC) = \text{Area}(ABCD) $ e la stessa altezza $ AH $.
  
  Sia $ \pi' $ un piano parallelo alla base che interseca entrambi i prismi. Le sezioni ottenute da questo piano, ovvero $A'B'C'$ e $A'B'C'D'$, sono congruenti alle rispettive basi, poiché i prismi sono tali per definizione, ossia i loro vertici corrispondenti sono uniti da segmenti paralleli e congruenti all’altezza.
  
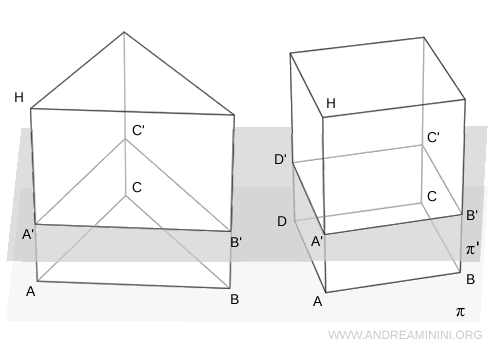
  Poiché le sezioni in ogni piano $ \pi' $ parallelo alla base hanno sempre la stessa area, secondo il principio di Cavalieri i due solidi hanno lo stesso volume. Quindi, i due prismi sono solidi equivalenti.

• Se due prismi hanno basi congruenti, i loro volumi sono proporzionali alle altezze.

  Dimostrazione. Il volume $V$ di un prisma qualsiasi si calcola come prodotto tra l’area della base e l’altezza (cioè la distanza perpendicolare tra le due basi):  $$ V = A_B \cdot h $$ dove $A_B$ è l’area della base e $h$ è l’altezza del prisma. Se due prismi hanno basi congruenti, ossia con la stessa area $A_B$, e volumi uguali, allora devono avere anche la stessa altezza:  $$ V_1 = V_2 \quad \text{e} \quad A_{B_1} = A_{B_2} \quad \Rightarrow \quad h_1 = h_2 $$ Viceversa, se i due prismi hanno basi congruenti ma volumi diversi, allora i volumi saranno proporzionali alle rispettive altezze:  $$ \frac{V_1}{V_2} = \frac{A_B \cdot h_1}{A_B \cdot h_2} = \frac{h_1}{h_2} $$ Quindi, a parità di base, il volume di un prisma è proporzionale alla sua altezza.

E così via