Piramide regolare

Una piramide regolare è una piramide retta la cui base è un poligono regolare, cioè un poligono con tutti i lati e gli angoli uguali.

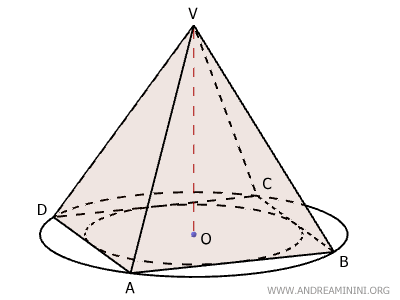
Questo significa che la base può essere un triangolo equilatero, un quadrato, un pentagono regolare, e così via.

Una piramide regolare ha queste caratteristiche

• Base regolare. La base della piramide è sempre un poligono regolare, quindi può essere inscrivibile e circoscrivibile a una circonferenza.
• Facce laterali congruenti. Tutte le facce laterali sono triangoli isosceli uguali tra loro.
• Altezza della piramide. La piramide è retta, quindi la sua altezza (OV) cade esattamente nel centro della base, indicato con O. Dove O è anche il centro del cerchio inscritto o circoscritto.
• Apotema della piramide. Ogni faccia laterale ha un’altezza chiamata apotema, che è la distanza tra il vertice della piramide e il punto medio del lato della base. Essendo una piramide retta, tutti gli apotemi sono congruenti.

La piramide regolare è una delle forme geometriche che hanno colpito di più l'uomo per la sua simmetria e semplicità. 

Nota. Basti pensare che le piramidi regolari sono utilizzate frequentemente in architettura e ingegneria. Il più noto esempio è la grande Piramide di Cheope in Egitto, basata su una struttura quasi perfettamente regolare.

Esempio di piramide regolare

Considero una piramide con base quadrata (ABCD), quindi un tetragono regolare.

Il vertice V si trova esattamente sopra il centro O della base. Il segmento OV è l'altezza della piramide ed è perpendicolare al piano della base ABCD.

Le quattro facce laterali sono triangoli isosceli congruenti.

$$ ABV \cong ADB \cong BCV \cong CDV $$

L'altezza delle facce laterali è l’apotema ed è congruente in ogni faccia. Ad esempio $ EV \cong FV $.

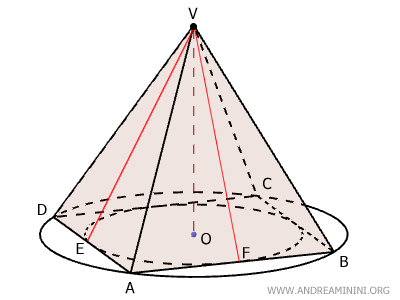
La piramide è perfettamente simmetrica, quindi posso inscrivere e circoscrivere la sua base in una circonferenza.

La dimostrazione

Una piramide regolare ha come base un poligono regolare.

Un poligono regolare è sempre inscrivibile e circoscrivibile in un cerchio.

Considero i punti di tangenza (E e F) tra la circonferenza interna e i lati del poligono.

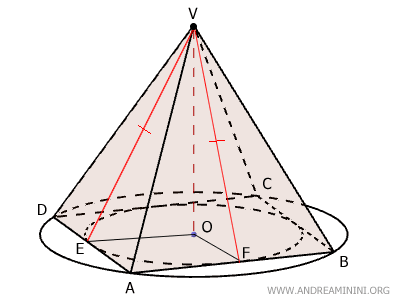
I segmenti EV e FV sono gli apotemi delle facce laterali ADV e ABV della piramide retta (vedi dimostrazione), quindi sono le altezze delle facce laterali e formano un angolo di 90° rispettivamente con i lati AD e AB della base.

I segmenti OE e OF sono congruenti perché sono il raggio della stessa circonferenza.

$$ OE \cong OF $$

Gli angoli $ E \hat{O} V \cong F \hat{O} V $ sono congruenti a 90° perché il segmento $ OV $ è l'altezza della piramide e, quindi, è perpendicolare alla base ABCD.

$$ E \hat{O} V \cong F \hat{O} V = 90° $$

Pertanto, i triangoli OEV e OFV sono congruenti per il primo criterio di congruenza perché hanno due lati congruenti e l'angolo tra di questi (90°) è congruente.

Questo significa che i segmenti $ EV \cong FV $, ossia gli apotemi della piramide, sono congruenti.

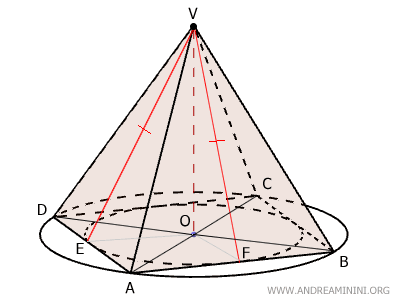
Poiché lo stesso ragionamento posso ripeterlo per ogni faccia laterale della piramide, deduco che gli apotemi sono congruenti in una piramide regolare.

Ora considero i segmenti $ OA \cong OB \cong OC \cong OD $ che sono congruenti tra loro perché sono il raggio della circonferenza esterna.

I triangoli $ OAV \cong OBV \cong OCV \cong ODV $ sono congruenti perché hanno due lati congruenti e l'angolo tra questi congruente (90°).

Quindi, i segmenti $ AV \cong BV \cong CV \cong DV $ sono congruenti.

Questo significa che i triangoli $ ABV $ e $ ADV $ sono triangoli isosceli perché hanno due lati congruenti.

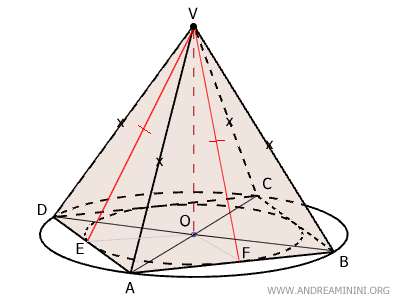
Pertanto, l'altezza (apotema) di questi triangoli coincide con la mediana e i punti E e F sono rispettivamente punti medi dei lati AD e AB.

$$ AE \cong ED \cong AF \cong BF $$

Per il terzo criterio di congruenza, i triangoli $ ABV \cong ADV $ sono congruenti perché hanno i lati congruenti nello stesso ordinte.

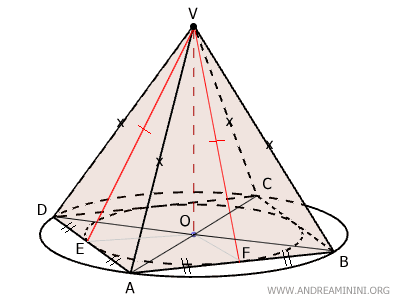
Poiché lo stesso ragionamento posso ripeterlo per ogni lato, posso affermare che le facce laterali della piramide sono triangoli isosceli congruenti tra loro.

Formule utili

Alcune formule fondamentali per calcolare le principali grandezze di una piramide regolare.

• Area della base
  Questa formula permette di calcolare l’area della base, che dipende dal numero di lati e dalla lunghezza di ciascun lato. \[ A_b = \frac{n \cdot l^2}{4} \cdot \cot \frac{180^\circ}{n} \] Dove \( n \) è il numero di lati della base, \( l \) è la lunghezza di un lato del poligono di base, \( \cot \) è la cotangente dell’angolo centrale associato al poligono regolare. Per una base quadrata, ad esempio, la formula si riduce a **\( A_b = l^2 \)**, poiché il quadrato ha un’area molto semplice da calcolare.

  Esempio. Se la base è un pentagono regolare con \( l = 5 \) cm, la sua area sarà:\[
  A_b = \frac{5 \cdot 5^2}{4} \cdot \cot \frac{180^\circ}{5} \approx 43.01 \text{ cm}^2 \]

• Area laterale
  Questa formula calcola l’area totale delle facce laterali della piramide.  \[ A_L = \frac{n \cdot l \cdot a}{2}  \] Dove \( n \) è il numero di lati della base, \( l \) è la lunghezza di un lato della base, \( a \) è l’apotema della piramide, ossia l’altezza di ciascun triangolo isoscele che forma le facce laterali. Poiché ogni faccia laterale è un triangolo isoscele, l’area di una singola faccia è \( \frac{l \cdot a}{2} \). Moltiplicando per il numero totale di lati \( n \), ottengo l’area laterale complessiva. 

  Esempio. Se la piramide ha base esagonale (\( n = 6 \)), ogni lato misura \( 4 \) cm e l’apotema della piramide è \( 7 \) cm, l’area laterale sarà: \[ A_L = \frac{6 \cdot 4 \cdot 7}{2} = 84 \text{ cm}^2 \]

• Volume della piramide
  Questa formula calcola il volume della piramide regolare. \[ V = \frac{A_b \cdot h}{3} \] Dove \( A_b \) è l’area della base, \( h \) è l’altezza della piramide, ovvero la distanza tra il vertice e il centro della base. La formula è simile a quella del volume di un prisma, con la differenza che il volume della piramide è un terzo di quello di un prisma con la stessa base e altezza. Questo perché la piramide "si restringe" verso il vertice, occupando meno spazio rispetto a un solido con base e altezza uguali.

  Esempio. Se una piramide ha una base quadrata con lato \( l = 6 \) cm, quindi \( A_b = 36 \) cm², e un’altezza di \( 10 \) cm, il volume sarà: \[ V = \frac{36 \cdot 10}{3} = 120 \text{ cm}^3 \]

E così via.