Cono troncato
Un cono troncato (o tronco di cono) è un solido che si ottiene tagliando un cono con un piano parallelo alla sua base, tagliando la parte superiore del cono.
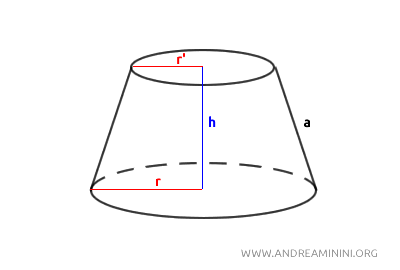
Questa operazione produce una figura geometrica solida che ha due basi circolari di diametro diverso, una maggiore (la base del cono originale) e una minore (la sezione del taglio).
I lati del cono troncato sono inclinati e convergono verso il centro della base maggiore, se immagino di estendere le linee.
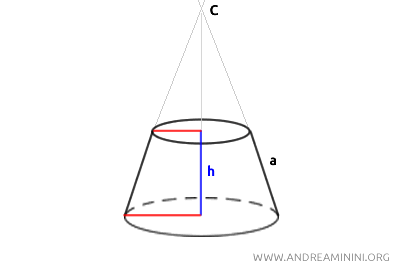
In altre parole, le linee immaginarie che ottengo prolungando l'apotema (a) del cono convergono verso la proiezione C del centro del cono troncato.
Le caratteristiche del tronco di cono
Il tronco di cono si ottiene tramite la rotazione completa a 360° di un trapezio lungo il lato perpendicolare alle basi, che corrisponde all'altezza (h) del solido.
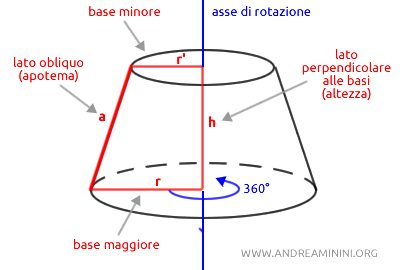
La retta a cui appartiene il lato perpendicolare alle basi è detta asse di rotazione del tronco di cono.
Il lato obliquo della rotazione è, invece, l'apotema (a) ovvero l'altezza della superficie laterale.
Nota. Questa forma è comune in molti contesti, dalla matematica alla vita quotidiana, dove può essere vista in oggetti come bicchieri di carta o lampade. Si trova in diverse strutture come cupole, torri o camini, dove la forma del cono troncato è utilizzata per la sua stabilità ed estetica. E' utilizzata anche negli altoparlanti per migliorare la direzionalità e l'efficienza della trasmissione del suono.
Le formule
Le caratteristiche principali di un cono troncato sono l'altezza (la distanza verticale tra le due basi), il raggio della base maggiore, e il raggio della base minore.
- Superficie di base
L'area di base deve essere calcolata sia sulla base maggiore AB che sulla base minore A'B che, essendo diverse, hanno un differente raggio (r≠r').
- Base maggiore $$ A_B = \pi r^2 $$
- Base minore $$ A'_B = \pi r'^2 $$
Nota. La somma delle superfici di base del tronco di cono è $$ A_B + A'_B = \pi r^2 + \pi r'^2 = \pi ( r^2 + r'^2 ) $$
- Superficie laterale
La superficie laterale AL si calcola usando l'apotema (a) ossia l'altezza della superficie laterale. $$ A_L = \pi a (r+r') $$Nota. La superficie laterale del tronco di cono è uguale al prodotto tra l'apotema e la somma delle semicirconferenze di base. $$ A_L = a \cdot ( \frac{1}{2} \cdot 2 \pi r + \frac{1}{2} \cdot 2 \pi r') $$ $$ A_L = a \cdot ( \pi r + \pi r') $$ $$ A_L = a \cdot \pi \cdot (r + r') $$
- Superficie totale
La superficie totale si calcola sommando le aree di base AB e A'B con la superficie laterale AL $$ A_T = A_L + A_B + A'_B $$ - Volume
Il volume del cono troncato si calcola usando la seguente formula: $$ V = \frac{1}{3} \pi h (r^2+r'^2+r \cdot r') $$ Dove h è l'altezza del cono troncato, r è il raggio della base maggiore, e r' è il raggio della base minore.Dimostrazione. Considero un cono grande di raggio $ R $, altezza $H$, da cui taglio via un cono piccolo di raggio $r' $ e altezza $h'$.
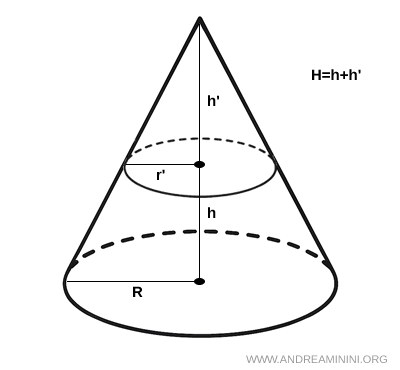
I due coni sono simili, quindi vale la proporzione $$ r':R = h':H $$ Dove $ H = h+h' $ posso vederla come la somma dell'altezza del cono più piccolo e quella del tronco di cono. $$ r':R = h':(h+h') $$ Quindi, riscrivendo la proporzione come una frazione ottengo: $$ \frac{r'}{R} = \frac{h'}{H} = \frac{h'}{h + h'} $$ Da questa ricavo l'altezza del cono più piccolo. $$ \frac{r'}{R} = \frac{h'}{h + h'} $$ $$ r' (h+h') = R h' $$ $$ r'h+r'h' = R h' $$ $$ r'h = R h' - r'h' $$ $$ r'h = h' (R - r') $$ $$ h' = \frac{r'}{R - r'} \cdot h $$ A questo punto, il volume dei due coni è il seguente:- $V_1 = \frac{1}{3} \pi R^2 (h + h')$ (volume del cono grande)
- $V_2 = \frac{1}{3} \pi r'^2 h'$ (volume del cono piccolo)
La relazione tra le aree dei cerchi in un cono e le distanze dal vertice
In un tronco di cono l'area del cerchio di base e del cerchio ottenuto da una sezione parallela stanno tra loro come i quadrati delle distanze dal vertice. \[\frac{A_1}{A_2} = \left( \frac{h_1}{h_2} \right)^2 \]
Dove:
- \( A_1 \) è l’area del cerchio di base (più grande);
- \( A_2 \) è l’area della sezione parallela alla base (più piccola);
- \( h_1 \) è la distanza tra il vertice e il piano di base;
- \( h_2 \) è la distanza tra il vertice e il piano della sezione.
Quando seziono un cono con un piano parallelo alla base, ottengo un secondo cerchio più piccolo, simile al cerchio di base.
Le figure simili mantengono proporzioni costanti nei loro lati corrispondenti, ma le aree si scalano al quadrato mentre i volumi al cubo del rapporto lineare.
Per questa ragione le aree di questi due cerchi, quello di base e quello sezionato, sono in una relazione ben precisa, fondata sulle distanze dal vertice del cono.
Esempio pratico
Considero un cono troncato in cui l'altezza del cono sia: \( h_1 = 12 \, \text{cm} \)
E la sezione avvenga a \( h_2 = 4 \, \text{cm} \) dal vertice
Allora, il rapporto tra le aree sarà:
\[ \frac{A_1}{A_2} = \left( \frac{12}{4} \right)^2 = 3^2 = 9 \]
Da questo deduco la proporzione tra le due aree.
\[ A_1 = 9 \cdot A_2 \]
In parole semplici: il cerchio di base è 9 volte più grande in area del cerchio sezionato.
Dimostrazione
Considero un cono e una sezione parallela alla base.
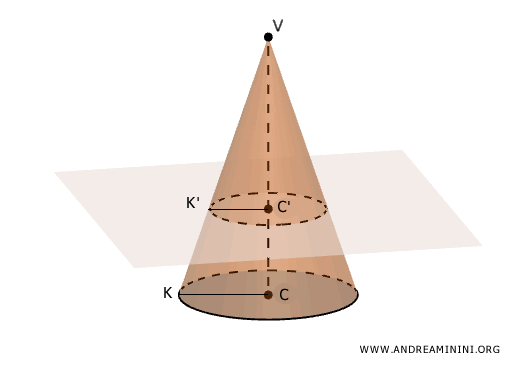
I triangoli VCK e VC'K' sono simili secondo il primo criterio di similitudine, perché hanno tutti gli angoli congruenti nello stesso ordine .
Quindi, i lati dei due triangoli hanno lo stesso rapporto di proporzionalità.
$$ VC : VC' = CK : C'K' $$
ovvero
$$ \frac{VC}{VC'} = \frac{CK}{C'K'} $$
Elevo al quadrato entrambi i membri
$$ \left( \frac{VC}{VC'} \right)^2 = \left( \frac{CK}{C'K'} \right)^2 $$
$$ \frac{VC^2}{VC'^2} = \frac{CK^2}{C'K'^2} $$
L'area di un cerchio è il raggio al quadrato per π=3.14, quindi il rapporto delle aree dei due cerchi è uguale al rapporto dei rispettivi raggi al quadrato.
$$ \frac{ \pi \cdot (CK)^2}{ \pi \cdot (C'K')^2} = \frac{ CK^2 }{ C'K'^2 } $$
Dove $ A= \pi \cdot (CK)^2 $ è l'area del cerchio di base e $ A_s = \pi \cdot (C'K')^2 $ è l'area del cerchio della sezione.
$$ \frac{ A}{ A_s} = \frac{ CK^2 }{ C'K'^2 } $$
Quindi, per la proprietà transitiva le aree dei cerchi hanno lo stesso rapporto dei quadrati delle rispettive distanze dal vertice V del cono.
$$ \frac{VC^2}{VC'^2} = \frac{CK^2}{C'K'^2} = \frac{ A}{ A_s} $$
$$ \frac{VC^2}{VC'^2} = \frac{ A}{ A_s} $$
Come volevasi dimostrare.
E così via.
