Teorema degli apotemi di una piramide retta
In una piramide retta, le altezze delle facce laterali (apotemi) sono tra loro congruenti e passano per i punti di tangenza della circonferenza inscritta con i lati della base.
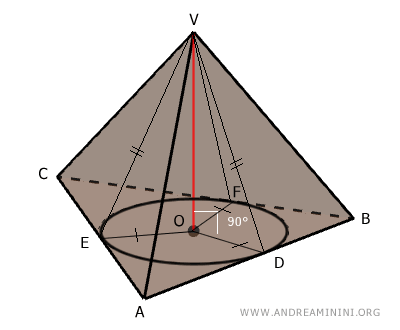
Le altezze delle facce laterali sono i segmenti perpendicolari tracciati dal vertice della piramide ai lati della base.
Questo teorema afferma che sono tra loro congruenti e passano per i punti di tangenza tra la circonferenza inscritta nella base e i lati della base stessa.
A cosa serve saperlo?
Il teorema garantisce una simmetria delle facce laterali nella piramide retta e mi permette di calcolare facilmente le altezze laterali conoscendo il raggio della circonferenza inscritta.
Nota. In particolar modo, se la base è un poligono regolare, la lunghezza delle altezze laterali può essere determinata usando semplici formule geometriche.
La dimostrazione
Considero una piramide retta
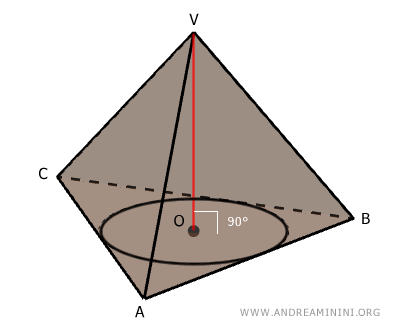
Quindi, per l'ipotesi iniziale il segmento OV è perpendicolare al piano della base ABC della piramide.
Traccio i segmenti che congiungono il centro della circonferenza con i punti di tangenza D, E, F.
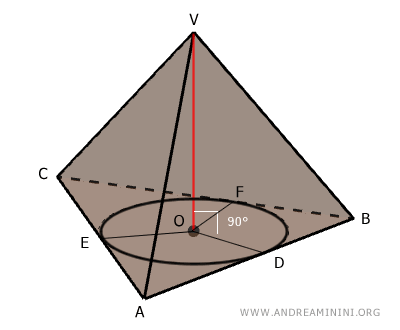
I segmenti OD, OE, OF sono congruenti tra loro perché sono il raggio della stessa circonferenza.
$$ OD \cong OE \cong OF $$
Inoltre i segmenti OD, OE, OF sono rispettivamente perpendicolari ai lati AB, AC, BC perché D, E, F sono punti di tangenza della circonferenza.
$$ OD \perp AB $$
$$ OE \perp AC $$
$$ OF \perp BC $$
Traccio i segmenti che congiungono ogni punto di tangenza D, E, F con il vertice V della piramide.
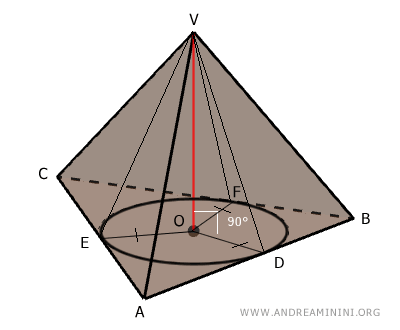
Per il teorema delle tre perpendicolari, sapendo che il segmento OV è perpendicolare alla base ABC e OD è perpendicolare al lato AB, anche il segmento VD della faccia laterale è perpendicolare al lato AB.
$$ VD \perp AB $$
Quindi, il segmento VD è l'altezza della faccia laterale ABV della piramide.
Posso affermare lo stesso anche per le altezze VE e VF delle altre facce laterali.
$$ VE \perp AC $$
$$ VF \perp BC $$
Ora i triangoli OVD e OVE hanno un lato coincidente (OV) e un lato congruente (OD≅OE), con l'angolo tra di essi congruente (90°), quindi per il primo criterio di congruenza sono triangoli congruenti.
$$ OVD \cong OVE $$
Essendo triangoli congruenti, anche i lati VE e VD sono congruenti.
$$ VD \cong VE $$
Quindi, le altezze delle due facce laterali sono congruenti.

Con lo stesso procedimento posso dimostrare che anche le altre altezze delle facce laterali, in questo caso OF, sono tra congruenti con OE e OD.
Ho dimostrato che in una piramide retta tutte le altezze delle facce laterali sono tra loro congruenti.
E così via.
