Ellisse

L'ellisse è una figura piana definita come il luogo dei punti in cui la somma delle distanze da due punti fissi F₁ e F₂, chiamati fuochi, è costante ed è maggiore della distanza tra i due fuochi.

Data un'ellisse con fuochi F₁ e F₂, per ogni punto P sull'ellisse, la somma delle distanze PF₁+PF₂ è costante.

$$ \overline{PF_1} + \overline{PF_1} = 2a $$

Ad esempio, se considero un punto qualsiasi P dell'ellisse e sommo le distanze del punto rispetto ai fuochi F₁ e F₂ ottengo sempre un valore costante k=2a

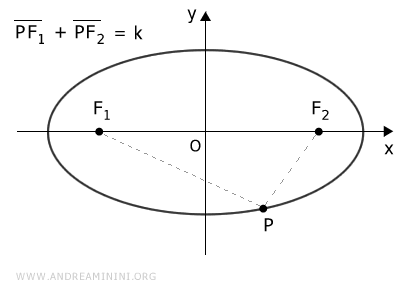
La distanza focale $ \overline{F_1F_2} $ è la distanza tra i due fuochi ed è sempre inferiore alla somma delle distanze PF₁+PF₂.

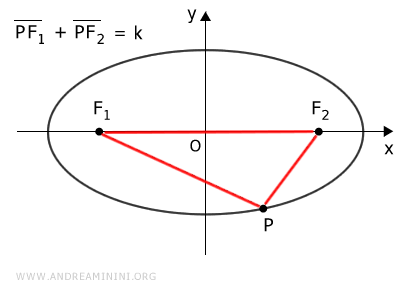
$$ \overline{PF_1} + \overline{PF_2} > \overline{F_1F_2}  $$

Nota. Questo è dovuto alla proprietà dei triangoli in base alla quale ogni lato del triangolo è inferiore alla somma degli altri due lati. I punti P, F₁ e F₂ formano un triangolo. Quindi, il lato F₁F₂ è inferiore alla somma degli altri due lati PF₁+PF₂.

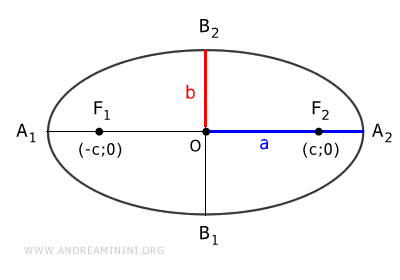
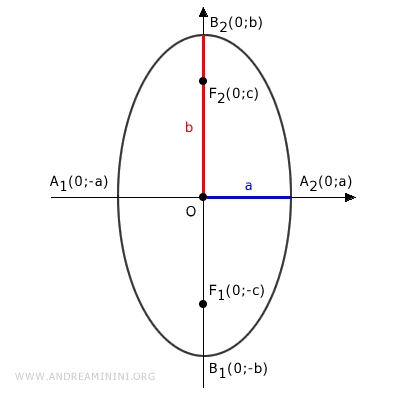
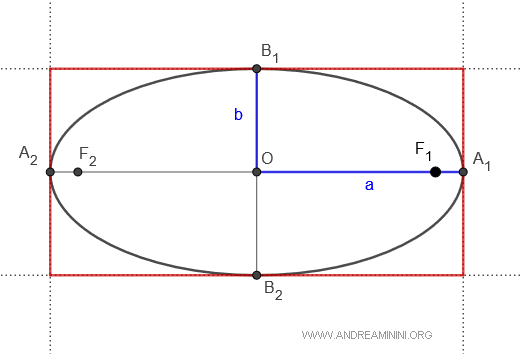
Gli assi di un'ellisse sono le due linee perpendicolari A₁A₂ e B₁B₂ che attraversano il suo centro (O), chiamate rispettivamente asse maggiore e asse minore.

• L'asse maggiore è la linea che passa per i fuochi ed è il diametro più lungo.
• L'asse minore è la linea perpendicolare all'asse maggiore ed è il diametro più corto.

 

Quindi, la distanza focale è $ \overline{F_1F_2} = 2c $, la lunghezza dell'asse maggiore è $ \overline{A_1A_2} = 2a $ e dell'asse minore è $ \overline{B_1B_2} = 2b $.

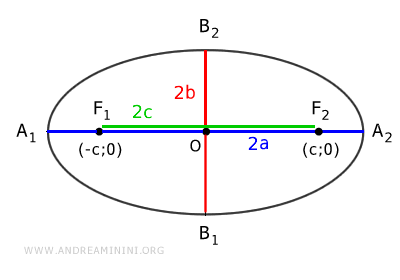
Il punto medio dell'asse maggiore è chiamato centro dell'ellisse.

Quando i due assi coincidono (a=b), l'ellisse diventa un cerchio.

I punti A₁, A₂, B₁, B₂ sono detti vertici dell'ellisse.

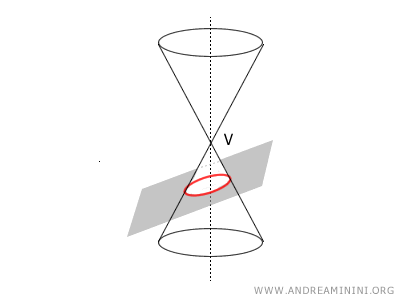
Dal punto di vista geometrico l'ellisse è una conica perché si ottiene facendo intersecare un piano orientato con un cono, in modo da formare un angolo compreso tra θ e π/2 rispetto all'asse del cono.

L'equazione dell'ellisse

L'ellisse ha una formula standard, detta equazione canonica (o normale) dell'ellisse, quando è centrata sull'origine del sistema di coordinate cartesiane:

\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]

Dove "a" è la metà della lunghezza dell'asse maggiore e "b" è la metà della lunghezza dell'asse minore, x e y sono le coordinate di un punto P qualsiasi dell'ellisse.

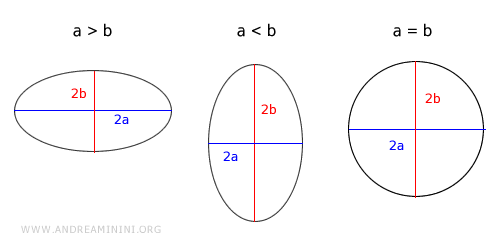
• Se a > b l'ellisse è orientata lungo l'asse x
• Se a < b l'ellisse è orientata lungo l'asse y
• Se a = b l'ellisse è un cerchio

Le formule per trovare le coordinate dei fuochi in una ellisse cambiano a seconda della relazione tra i semiassi "a" e "b".

• Se a>b $$ F_1 ( - \sqrt{ a^2 - b^2 } ;0 ) $$ $$ F_2 ( \sqrt{ a^2 - b^2 } ;0 ) $$
• Se a<b $$ F_1 (0; - \sqrt{ b^2 - a^2 } ) $$ $$ F_2 ( 0; \sqrt{ b^2 - a^2 } ) $$

Dove "a" e "b" sono le lunghezze dei semiassi dell'ellisse.

 

I vertici dell'ellisse, invece, si trovano alle seguenti coordinate (x;y)

$$ A_1 ( -a; 0) $$

$$ A_2 ( a; 0) $$

$$ B_1 ( 0; -b) $$

$$ B_2 ( 0; b) $$

Questi ultimi sono i punti di intersezione con gli assi cartesiani.

La forma più o meno schiacciata dell'ellisse è detta eccentricità (e) ed è determinata dalla seguente formula

• Se a>b la formula dell'eccentricità è $$ e = \frac{c}{a} $$
• Se a<b la formula dell'eccentricità è $$ e = \frac{c}{b} $$
• Se a=b si può usare indiferentemente una delle precedenti formule

Dove "a" è il semiasse maggiore (metà della lunghezza dell'asse maggiore 2a), "b" è il semiasse minore (metà della lunghezza dell'asse minore 2b) e "c" è la distanza focale (la distanza di ciascun fuoco dal centro dell'ellisse)

La distanza "c" di ciascun fuoco dal centro dell'ellisse si ottiene usando il teorema di Pitagora.

$$ c = \sqrt{a^2 -b^2} $$

In entrambi i casi, poiché c<a e c<b deduco che l'eccentricità è un parametro compreso tra 0 e 1.

$$ 0 \le e < 1 $$

Quanto più l'eccentricità tende a 1, tanto più l'ellisse è schiacciata sull'asse x.

Viceversa quanto più l'eccentricità tende a 0, tanto più l'ellisse si avvicina a un cerchio. Con e=0 l'ellisse diventa un cerchio.

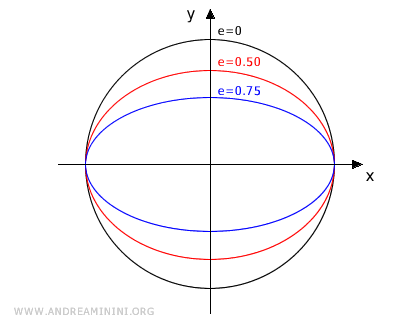
In altre parole, l'eccentricità può essere vista come la misura della "rotondità" dell'ellisse, che varia tra 0 (circonferenza) e 1 (ellissi molto allungate).

Nota. Quindi, la circonferenza può essere considerata come un caso particolare di ellisse in cui i due fuochi coincidono con il centro della circonferenza.

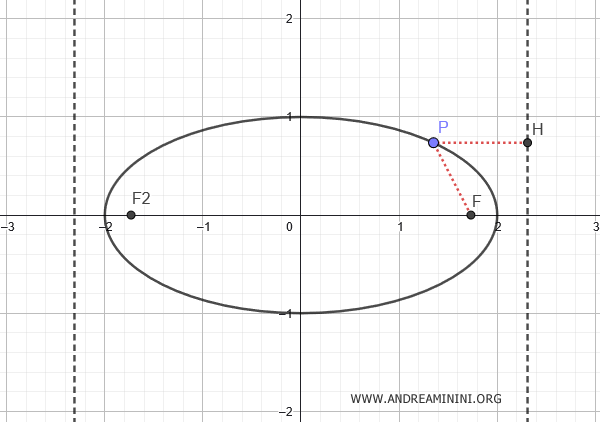
Ogni ellisse ha due fuochi e due rette direttrici simmetriche e perpendicolari all'asse focale.

Se l'asse focale è l'asse x, le rette direttrici sono le seguenti:

$$ x = \pm \frac{a^2}{c} $$

Se l'asse focale è l'asse y, le rette direttrici sono:

$$ y = \pm \frac{b^2}{c} $$

In generale, come per ogni conica, dato un punto $ P(x;y) $ dell'ellisse il rapporto tra la distanza $ \overline{PF} $ del un punto dal fuoco e quella $ \overline{PH} $ del punto dalla direttrice è costante, ed è uguale all'eccentricità.

$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$

Un esempio pratico

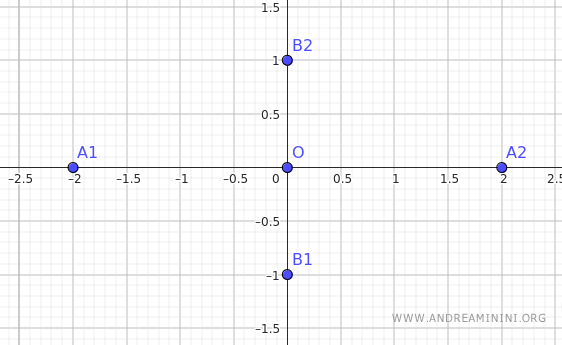
Provo a costruire una ellisse considerando come semiasse orizzontale e verticale a=2 e b=1

Per semplicità il centro dell'ellisse coincide con l'origine degli assi cartesiani O(0;0).

Quindi, sapendo che a=2 e b=1, i vertici dell'ellisse sono A₁(-2;0), A₂(2;0), B₁(0;-1), B₂(0;1),

Per trovare i fuochi dell'ellisse utilizzo le formule seguenti:

$$ \begin{cases} F_1 ( - \sqrt{ a^2 - b^2 } ;0 ) \\ \\ F_2 ( \sqrt{ a^2 - b^2 } ;0 ) \end{cases} $$

Sostituisco in entrambe i valori dei semiassi a=2 e b=1

$$ \begin{cases} F_1 ( - \sqrt{ 2^2 - 1^2 } ;0 ) \\ \\ F_2 ( \sqrt{ 2^2 - 1^2 } ;0 ) \end{cases} $$

$$ \begin{cases} F_1 ( - \sqrt{ 4 - 1 } ;0 ) \\ \\ F_2 ( \sqrt{ 4 - 1 } ;0 ) \end{cases} $$

$$ \begin{cases} F_1 ( - \sqrt{ 3 } ;0 ) \\ \\ F_2 ( \sqrt{ 3 } ;0 ) \end{cases} $$

Pertanto la distanza dei fuochi dal centro dell'ellisse è c=√3

I due fuochi dell'ellisse si trovano alle coordinate F₁(-√3;0) e F₂(√3;0)

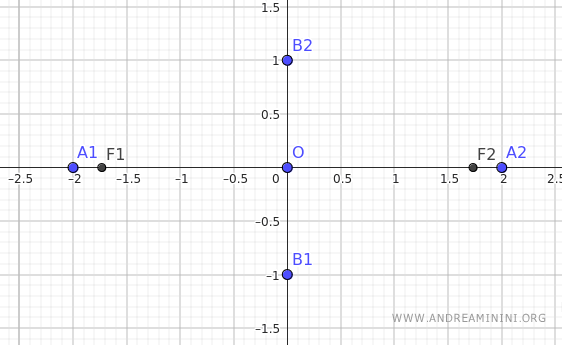
A questo punto, una volta noto il valore "c", posso calcolare l'eccentricità dell'ellisse.

Poiché a>b utilizzo la formula seguente

$$ e = \frac{c}{a} = \frac{ \sqrt{3} }{2} ≈ 0.86 $$

Infine, utilizzo l'equazione canonica dell'ellisse per trovare i vari punti dell'ellisse.

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{2^2} + \frac{y^2}{1^2} = 1 $$

$$ \frac{x^2}{4} + y^2 = 1 $$

Ricavo la componente y

$$ y^2 = 1-\frac{x^2}{4} $$

Poi applico la radice quadrata in entrambi i membri dell'equazione

$$ \sqrt{y^2} = \sqrt{ 1-\frac{x^2}{4}} $$

$$ y = \pm \sqrt{ 1-\frac{x^2}{4}} $$

In questa forma l'equazione mi permette di trovare la componente y di ogni punto a partire dalla componente x nell'intervallo [-a,a] ossia [-2,2].

x	y
-2	0
-1	±0.86
0	±1
1	±0.86
2	0

Questi sono i punti appena trovati

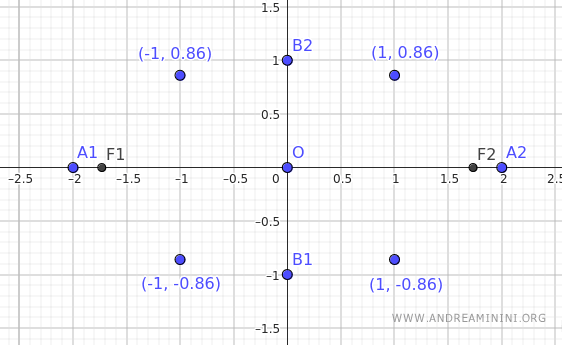
Già da questi pochi punti posso immaginare la forma dell'ellisse.

Ripetendo i calcoli posso trovare altri punti dell'ellisse per completare il disegno.

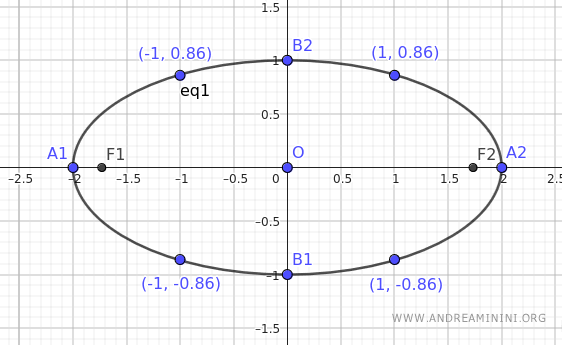
Nota. In questo esempio ho utilizzato Geogebra per costruire l'ellisse. E' un buon metodo per imparare le proprietà dell'ellisse "sul campo" provando a cambiare i valori dei semiassi.

La dimostrazione

Le ellissi più semplici sono quelle che hanno il centro O nell'origine degli assi cartesiani e i fuochi sull'asse x delle ascisse o sull'asse y delle ordinate.

A] Ellisse con i fuochi sull'asse x

In questo caso i fuochi si trovano sull'asse delle ascisse e l'asse maggiore è l'asse orizzontale ossia a>b.

$$ a>b $$

Per ipotesi i fuochi si trovano alle coordinate F₁(-c;0) e F₂(c;0) alla stessa distanza dal centro dell'ellisse.

I due fuochi distano tra loro 2c.

$$ \overline{F_1F_2} = 2c $$

Per definizione l'ellisse è il luogo dei punti per i quali la somma delle distanze ai due fuochi è costante.

$$ \overline{PF_1} + \overline{PF_2} = k $$

Qual è il valore della costante k?

Per scoprirlo prendo in considerazione come punto P il vertice A₂ sull'asse maggiore x

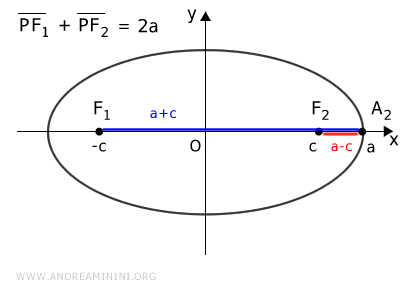
In questo caso la distanza dai fuochi è la seguente.

$$ \overline{A_2F_1} = a+c $$

$$ \overline{A_2F_2} = a-c $$

Sommo le due distanze e ottengo il valore k=2a

$$ \overline{A_2F_1} + \overline{A_2F_2} = k $$

$$ (a+c) + (a-c) = k $$

$$ a+c + a-c = k $$

$$ 2a = k $$

Poiché il valore k è costante per qualsiasi punto dell'ellisse, deduco che la somma delle distanze PF₁+PF₂ è sempre uguale a 2a

$$ \overline{PF_1} + \overline{PF_2} = 2a $$

Come trovare le coordinate dei fuochi?

Per capirlo prendo in considerazione il vertice B₂ sull'asse minore y sapendo che k=2a.

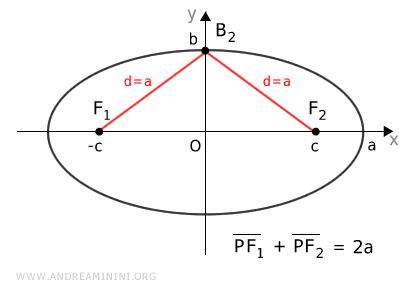
La somma delle distanze del punto B₂ dai fuochi è uguale a 2a

$$ \overline{B_2F_1} + \overline{B_2F_2} = 2a $$

In questo caso la distanza da ciascun fuoco è la stessa, perché il punto B₂ giace su un asse di simmetria dell'ellisse.

$$ \overline{B_2F_1} = \overline{B_2F_2} = a $$

Questo significa che la distanza (d=a) tra un vertice sull'asse y e uno dei fuochi è la metà della lunghezza dell'asse maggiore (2a).

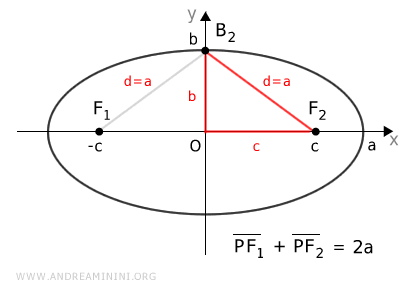
A questo punto per calcolare il valore della componente c applico il Teorema di Pitagora sul triangolo rettangolo OB₂F₂ sapendo che l'ipotenusa è d=a mentre i cateti hanno lunghezze pari ad "a" e "c"

$$ a^2 = b^2 + c^2 $$

Questo mi permette di ricavare la componente "c"

$$ c^2 = a^2 - b^2 $$

$$ \sqrt{ c^2 } = \sqrt{ a^2 - b^2 } $$

$$ c = \sqrt{ a^2 - b^2 } $$

Pertanto, le coordinate dei fuochi sono le seguenti

$$ F_1 ( - \sqrt{ a^2 - b^2 } ;0 ) $$

$$ F_2 ( \sqrt{ a^2 - b^2 } ;0 ) $$

Come si ottiene l'equazione dell'ellisse?

Considero un punto P(x;y) qualsiasi lungo l'ellisse.

 

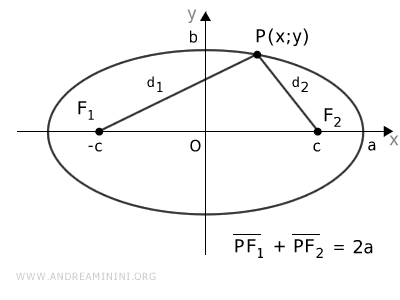
Utilizzando il teorema di Pitagora posso calcolare le distanze del punto P dai fuochi F₁ e F₂ dell'ellisse

$$ d_1 = \sqrt{(x+c)^2+y^2} $$

$$ d_2 = \sqrt{(x-c)^2+y^2} $$

Sapendo che in ogni punto P dell'ellisse la somma delle distanze d₁+d₂ è costante ed è uguale a 2a

$$ d_1 + d_2 = 2a $$

$$ \sqrt{(x+c)^2+y^2} + \sqrt{(x-c)^2+y^2} = 2a $$

Se manipolo algebricamente la somma usando la relazione d₁+d₂=2a e il teorema di Pitagora c²=a²-b², dopo alcune semplificazioni e rielaborazioni che possono diventare un po' laboriose, arrivo all'equazione canonica dell'ellisse

Sposto una delle due radici nel membro di destra

$$ \sqrt{(x+c)^2+y^2} = 2a - \sqrt{(x-c)^2+y^2} $$

Elevo entrambi i membri al quadrato

$$ ( \sqrt{(x+c)^2+y^2} )^2 = ( 2a - \sqrt{(x-c)^2+y^2} )^2 $$

$$ (x+c)^2+y^2 = 4a^2 - 2 \cdot 2a \cdot \sqrt{(x-c)^2+y^2} + ( \sqrt{(x-c)^2+y^2} )^2 $$

$$ (x+c)^2+y^2 = 4a^2 - 4a \cdot \sqrt{(x-c)^2+y^2} + (x-c)^2+y^2 $$

Sviluppo i quadrati dei binomi

$$ x^2+2xc+c^2+y^2 = 4a^2 - 4a \cdot \sqrt{(x-c)^2+y^2} + x^2-2xc+c^2+y^2 $$

Poi semplico

$$ 2xc = 4a^2 - 4a \cdot \sqrt{(x-c)^2+y^2} -2xc $$

$$ 2xc + 2xc - 4a^2 = - 4a \cdot \sqrt{(x-c)^2+y^2} $$

$$ 4xc - 4a^2 = - 4a \cdot \sqrt{(x-c)^2+y^2} $$

Elevo al quadrato entrambi i membri dell'equazione per eliminare la radice quadrata

$$ ( 4xc - 4a^2 )^2 = (- 4a \cdot \sqrt{(x-c)^2+y^2} )^2 $$

$$ 16x^2c^2 +16a^4- 32a^2xc = 16 a^2 \cdot [ (x-c)^2+y^2 ] $$

Divido entrambi i membri dell'equazione per 16

$$ \frac{ 16x^2c^2 +16a^4- 32a^2xc}{16} = \frac{ 16 a^2 \cdot [ (x-c)^2+y^2 ] } {16} $$

$$ x^2c^2 +a^4- 2a^2xc = a^2 \cdot [ (x-c)^2+y^2 ] $$

$$ \frac{ x^2c^2 +a^4- 2a^2xc }{a^2} = (x-c)^2+y^2 $$

$$ \frac{ x^2c^2}{a^2} + \frac{a^4}{a^2}- \frac{2a^2xc}{a^2} = (x-c)^2+y^2 $$

$$ \frac{ x^2c^2}{a^2} + a^2 - 2xc = (x-c)^2+y^2 $$

Sviluppo il quadrato del binomio e semplifico

$$ \frac{ x^2c^2}{a^2} + a^2 - 2xc = x^2+c^2-2xc+y^2 $$

$$ \frac{ x^2c^2}{a^2} + a^2 = x^2+c^2+y^2 $$

Sposto i termini noti nel membro di destra

$$ \frac{ x^2c^2}{a^2}-x^2-y^2 = c^2- a^2 $$

$$ x^2 \cdot ( \frac{ c^2}{a^2}-1) -y^2 = c^2- a^2 $$

$$ x^2 \cdot ( \frac{ c^2-a^2}{a^2}) -y^2 = c^2- a^2 $$

Sapendo che c²=a²-b² sostituisco c²-a²=-b²

$$ x^2 \cdot \frac{ -b^2}{a^2}-y^2 = -b^2 $$

$$ - \frac{ x^2b^2}{a^2}-y^2 = -b^2 $$

Poi moltiplico entrambi i membri per -1 in modo da cambiare il segno

$$ [- \frac{ x^2b^2}{a^2}-y^2 ] \cdot (-1) = -b^2 \cdot (-1) $$

$$ \frac{ x^2b^2}{a^2}+y^2= b^2 $$

Infine, divido entrambi i membri per b²

$$ \frac{1}{b^2} \cdot [ \frac{ x^2b^2}{a^2}+y^2 ]= \frac{1}{b^2} \cdot b^2 $$

$$ \frac{ x^2b^2}{a^2b^2}+ \frac{y^2}{b^2}= 1 $$

Il risultato finale è l'equazione canonica dell'ellisse.

$$ \frac{ x^2}{a^2}+ \frac{y^2}{b^2}= 1 $$

Dove x e y sono le coordinate di un punto qualsiasi P dell'ellisse mentre a e b sono le lunghezze dei semiassi dell'ellisse.

B] Ellisse con i fuochi sull'asse y

In questo caso i fuochi si trovano sull'asse y delle ordinate e l'asse verticale dell'ellisse è più lungo dell'asse orizzontale. Quindi, l'ipotesi di partenza è

$$ b > a $$

I due fuochi si trovano alle coordinate F₁(0;-c) e F₂(0;c) alla stessa distanza dal centro dell'ellisse.

La lunghezza dell'asse maggiore è 2b.

Quindi, la somma delle distanze di ogni punto P deve essere uguale a 2b.

$$ \overline{PF_1} + \overline{PF_2} =2b $$

La dimostrazione che la somma è uguale a 2b è simile al caso precedente.

Se considero il punto B₂, le distanze dai due fuochi sono le seguenti:

$$ \overline{B_2F_1} = b+c $$

$$ \overline{B_2F_2} = b-c $$

Sommo le due distanze e ottengo il valore k=2b

$$ \overline{B_2F_1} + \overline{B_2F_2} = k $$

$$ (b+c) + (b-c) = k $$

$$ b+c + b-c = k $$

$$ 2b = k $$

Sapendo che in una ellisse la somma delle distanze dai fuochi è sempre costante, deduco che la somma sia 2b in ogni punto dell'ellisse.

Poiché b>a, in questo caso i fuochi dell'ellisse si trovano sull'asse y

$$ F_1 (0; - \sqrt{ b^2 - a^2 } ) $$ $$ F_2 ( 0; \sqrt{ b^2 - a^2 } ) $$

L'equazione canonica per tracciare l'ellisse è sempre la stessa.

$$ \frac{ x^2}{a^2}+ \frac{y^2}{b^2}= 1 $$

Valgono le stesse proprietà e considerazioni già fatte nella dimostrazione precedente.

La storia dell'ellisse

L'ellisse fu studiata per la prima volta dai matematici greci.

Nel IV secolo a.C. Menaechmus, un allievo di Eudosso e contemporaneo di Platone, è noto per la scoperta delle sezioni coniche, tra cui l'ellisse. Ottenne l'ellisse sezionando un cono con un piano inclinato non parallelo alla base.

Il contributo più significativo alla teoria delle coniche fu dato nel III secolo a.C. da Apollonio che scrisse un'opera in otto libri chiamata "Coniche". Apollonio sistematizzò e ampliò le conoscenze esistenti sulle coniche, introducendo i termini ellisse, parabola e iperbole. Fu anche il primo a ricavare tutte le coniche da un'unico cono. In precedenza si usavano coni diversi per ottenere le varie coniche.

Durante il Medioevo, le conoscenze matematiche degli antichi greci furono preservate e sviluppate dagli studiosi arabi. L'ellisse continuò ad essere studiata e le opere greche furono tradotte in arabo e poi in latino.

Nel XVII secolo, l'ellisse divenne fondamentale nella descrizione delle orbite planetarie. Keplero scoprì che le orbite dei pianeti attorno al Sole non erano circolari ma ellittiche.

Con lo sviluppo della geometria analitica, René Descartes introdusse il concetto di coordinate cartesiane, permettendo la rappresentazione algebrica delle curve. L'equazione standard dell'ellisse, \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \), deriva da questo approccio.

Successivamente l'ellisse ha trovato applicazioni in numerosi campi della scienza e dell'ingegneria. Ad esempio, gli specchi ellittici e lo studio delle traiettorie ellittiche degli oggetti in moto sotto l'azione di forze centrali.

La simmetria dell'ellisse

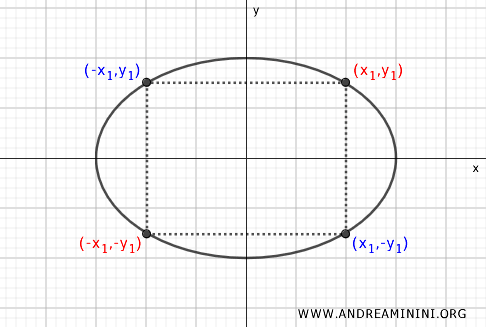
L'ellisse ha la proprietà geometrica di essere speculare rispetto ai suoi due assi principali (asse maggiore e asse minore)

La simmetria dell'ellisse implica che per ogni punto sull'ellisse, ce n'è un altro situato simmetricamente rispetto all'asse maggiore e all'asse minore.

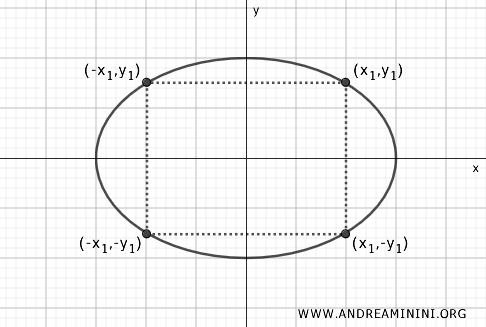
Nota. Questa proprietà deriva dal fatto che le variabili x e y sono elevate al quadrato. Il quadrato di un numero è sempre uguale al quadrato del numero opposto. Quindi $ x^2 = (-x^2) $ e $ y^2 = (-y)^2 $. Questo significa che l'ellisse ha come asse di simmetria l'asse sia l'asse x $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Leftrightarrow \frac{(-x)^2}{a^2} + \frac{y^2}{b^2} = 1 $$ e sia l'asse y $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Leftrightarrow \frac{x^2}{a^2} + \frac{(-y)^2}{b^2} = 1 $$

Esistono tre tipi di simmetrie nell'ellisse:

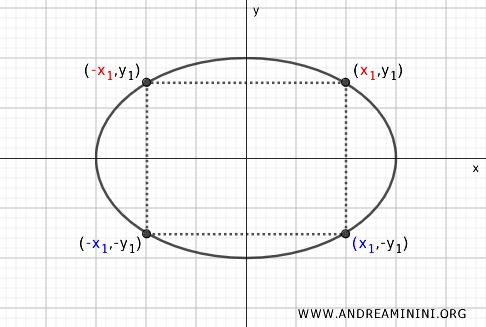
• Simmetria rispetto all'asse y
  Considero un punto \( P(x, y) \) sull'ellisse. Il punto simmetrico rispetto all'asse y è \( P'(-x, y) \). Questa proprietà significa che l'ellisse è identica se riflessa lungo l'asse y.
  
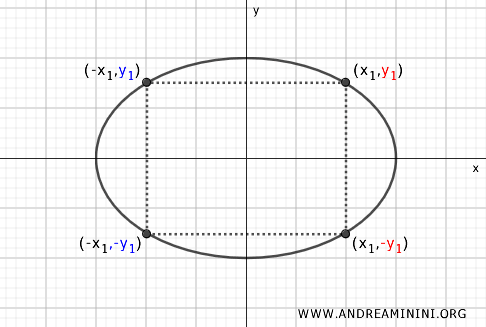
• Simmetria rispetto all'asse x
  Allo stesso modo, per un punto \( P(x, y) \), il punto simmetrico rispetto all'asse x è \( P'(x, -y) \). Anche qui, l'ellisse mantiene la sua forma se riflessa lungo l'asse x.
  
• Simmetria rispetto all'origine degli assi
  Un altro aspetto della simmetria dell'ellisse è che per un punto \( P(x, y) \), esiste un punto simmetrico rispetto al centro, dato da \( P'(-x, -y) \). Questo significa che l'ellisse può essere riflessa rispetto all'origine degli assi e apparirà identica.
  

Osservazioni

Alcune osservazioni e note a margine sulle ellissi

• L'ellisse è inscritta in un rettangolo
  Ogni ellisse è inscritta in un rettangolo che passa per i vertici e ha i lati di lunghezza 2a e 2b.
  
• L'ellisse è una conica
  L'ellisse appartiene alla famiglia delle coniche, come le iperbole, il cerchio e le parabole, perché può essere ottenuta come sezione, facendo intersecare un piano inclinato con un cono circolare.
• Se l'eccentricità è nulla, l'ellisse diventa un cerchio
  Se l'ellisse ha un'eccentricità pari a zero (e=0) coincide con una circonferenza e i due fuochi si trovano entrambi al centro della circonferenza.
• Il diametro dell'ellisse
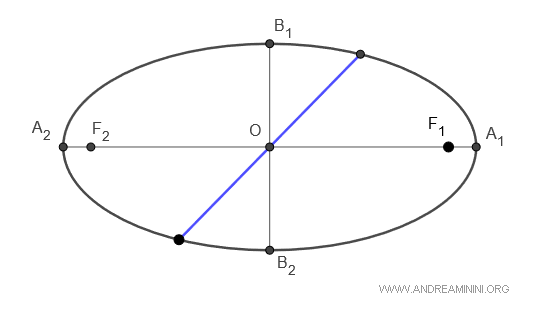
  Ogni corda che passa per il centro dell'ellisse è detta "diametro".
  
• La proprietà focale dell'ellisse
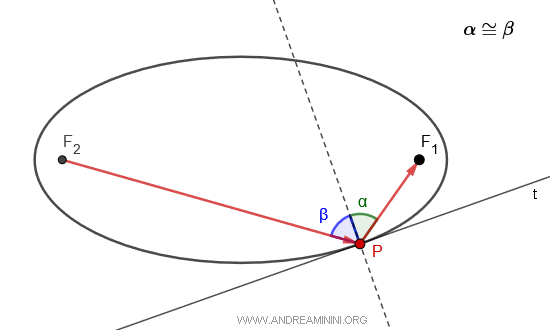
  In ogni punto P di una ellisse la bisettrice dell'angolo formato dai segmenti che congiungono il punto con i fuochi F₁ e F₂ è perpendicolare alla tangente del punto P sulla curva. In altre parole, i raggi focali $ \overline{PF_1} $ e $ \overline{PF_2} $ che congiungono i fuochi con un punto P dell'ellisse formano due angoli congruenti $ \alpha \cong \beta $ rispetto alla perpendicolare della retta tangente (t) nel punto P.
  
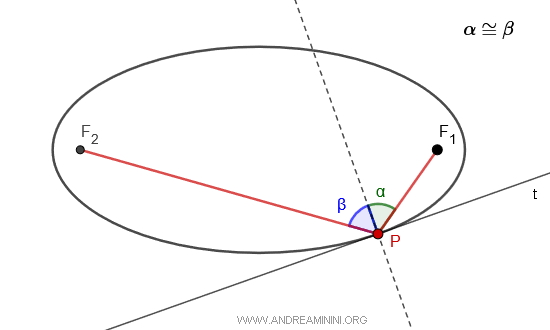
  Questo significa che qualsiasi sorgente luminosa che ha origine da un fuoco verso il punto P, viene riflessa raggiunge l'altro fuoco.
  
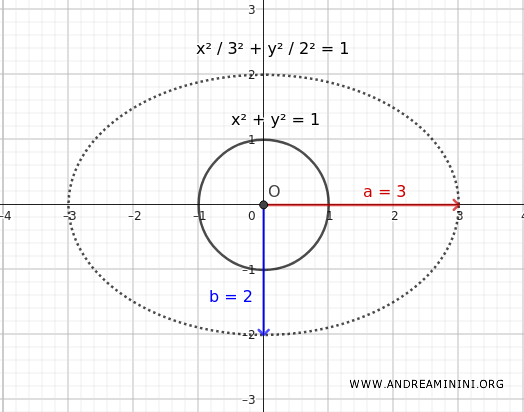
• L'ellisse è una dilatazione della circonferenza
  L'equazione di una circonferenza centrata nell'origine è $$ x^2+y^2=1 $$ Applico una dilatazione di $ ax $ e $ by $ sulle variabili $$ \begin{cases} x'=ax \\ \\ y'=bx \end{cases} $$ Ricavo x e y $$ \begin{cases} x = \frac{x'}{a} \\ \\ y = \frac{y'}{b} \end{cases} $$ Poi sostituisco $ x $ e $ y $ alle variabili dell'equazione della circonferenza $$ x^2+y^2=1 $$ $$ (\frac{x'}{a})^2+(\frac{y'}{b})^2=1 $$ $$ \frac{x'^2}{a^2}+\frac{y'^2}{b^2}=1 $$ Il risultato finale è l'equazione canonica di un'ellisse centrata sull'origine.
  

  Il rapporto tra le aree è proporzionale. La superficie s della circonferenza centrata nell'origine e quella s' dell'ellisse ottenuta con una dilatazione $ a $, $ b $ sono in proporzione $$ s' = s \cdot ab $$ dove $ s = \pi \cdot 1^2 = \pi $ se la circonferenza ha raggio unitario e, di conseguenza, l'area dell'ellisse è la seguente: $$ s' = \pi' \cdot ab $$

E così via.