Iperbole
L'iperbole è una curva piana in cui la differenza delle distanze di ogni punto P dai due punti fissi F1 e F2, chiamati fuochi, è costante (2a) in valore assoluto. $$ | \overline{PF}_1 - \overline{PF}_2 | = 2a $$ Dove 2a è la distanza tra i due vertici dell'iperbole.
Una iperbole è una curva aperta suddivisa in due rami che tendono a infinito lungo la direzione di due rette oblique dette asintoti.
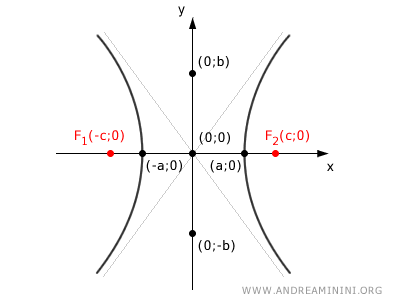
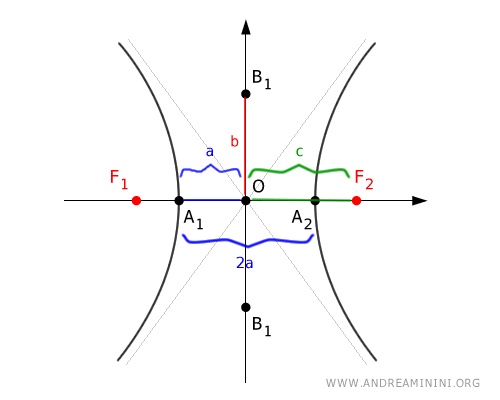
I due vertici (-a;0) e (a;0) dell'iperbole distano tra loro un segmento lungo 2a.
La distanza tra ogni vertice e il centro dell'iperbole è, invece, pari ad "a".
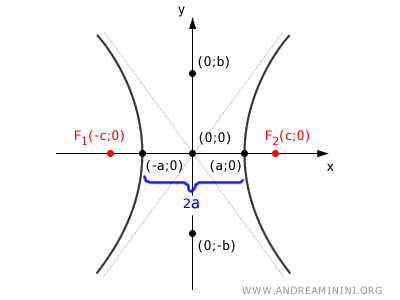
Se prendo due punti qualsiasi P1 e P2 dell'iperbole la differenza delle loro distanze dai fuochi in valore assoluto è sempre la stessa.
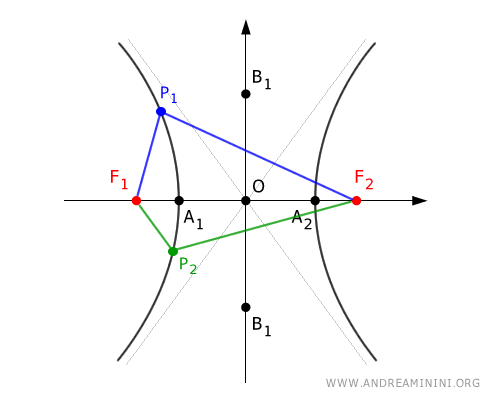
In altre parole ogni coppia di punti dell'iperbole soddisfa questa relazione
$$ | \overline{P_1F_1} - \overline{P_1F_2} | = | \overline{P_2F_1} - \overline{P_2F_2} | $$
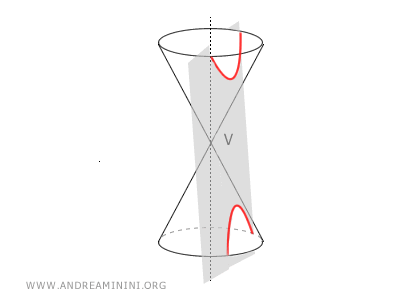
Nota. L'iperbole è una conica perché può essere ottenuta sezionando un cono circolare con un piano che abbia un angolo minore all'apertura del cono.
Le caratteristiche
L'iperbole è un luogo geometrico dove i punti del piano soddisfano una specifica proprietà, quella di mantenere costante la differenza rispetto a due punti fissi F1 e F2 detti fuochi.
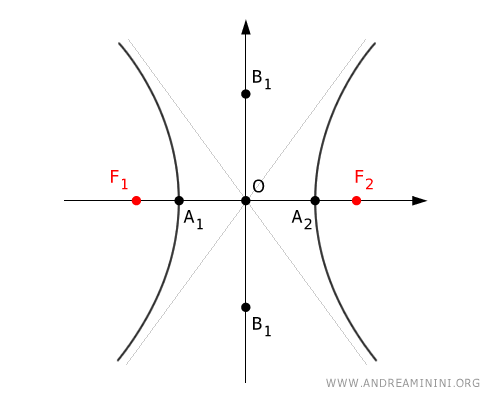
La retta che passa tra i fuochi F1 e F2 è detta asse principale (o asse trasverso).
I punti di intersezione A1 e A2 dell'iperbole con l'asse principale sono detti vertici reali.
Nota. In alcuni testi per "asse trasverso" si intende anche il segmento tra i vertici reali A1 e A2 ossia la distanza tra i due vertici che è sempre pari a 2a. $$ \overline{A_1A_2} = 2a $$ In questi casi, per semiasse trasverso si intende la distanza "a" tra un vertice e il centro O dell'iperbole. $$ \overline{OA_1} = \overline{OA_2} = a $$
L'asse del segmento F1F2 è, invece, detto asse secondario (o asse non trasverso).
I due punti B1 e B2 sull'asse secondario sono detti vertici non reali, perché non sono punti di intersezione dell'iperbole ma contribuiscono a determinare l'inclinazione degli asintoti.
Il punto di intersezione O dei due assi, principale e secondario, è detto centro dell'iperbole.
E' il punto medio $ O $ del segmento \overline{F_1F_2} tra i due fuochi.
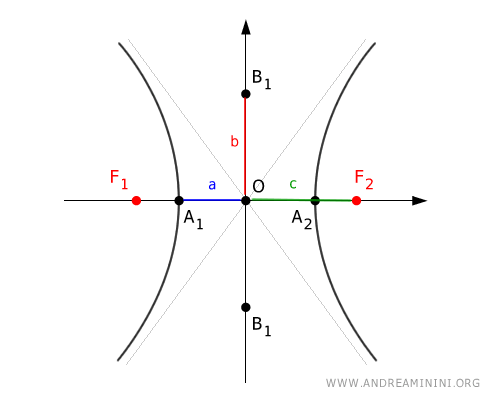
Nel grafico i termini "a", "b" e "c" indicano rispettivamente le distanze dal centro O dei vertici reali, non reali e dei fuochi.
Gli asintoti sono le rette oblique che passano per il centro dell'iperbole O e sono tangenti alla curva all'infinito.
La distanza tra i due fuochi $ F_1 $ e $ F_2 $ è detta distanza focale.
$$ 2c = \overline{F_1F_2} $$
Dato un punto $ P $ sull'iperbole la differenza in valore assoluto dei segmenti $ | \overline{PF}_1 - \overline{PF}_2 | $ è costante ed è pari a $ 2a $
$$ | \overline{PF}_1 - \overline{PF}_2 | = 2a $$
Il punto $ P $ e i fuochi $ F_1 $ e $ F_2 $ formano un triangolo $ PF_1F_2 $ in cui il lato più lungo è sempre $ \overline{F_1F_2} = 2c $.
La differenza degli altri due lati del triangolo è invece $ | \overline{PF}_1 - \overline{PF}_2 | = 2a $
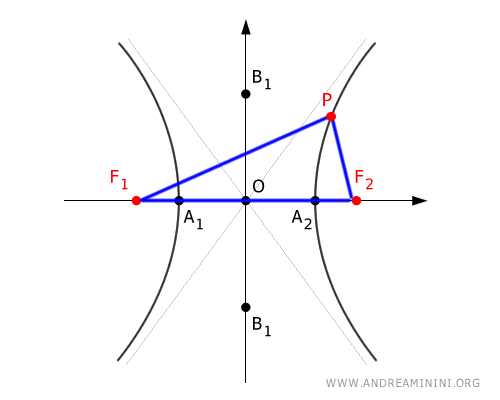
Sapendo che, secondo il teorema delle diseguaglianze triangolari, in un triangolo un lato è sempre maggiore alla differenza degli altri due lati, deduco che 2c>2a
$$ 2c > 2a $$
ovvero
$$ c > a $$
Pertanto, in un iperbole la distanza $ c $ tra un fuoco è il centro $ O $ dell'iperbole è sempre maggiore alla distanza tra un vertice e il centro.
L'equazione canonica dell'iperbole
Per rappresentare un'iperbole è comune utilizzare un sistema di riferimento cartesiano in cui:
- il centro dell'iperbole corrisponde all'origine O(0;0)
- l'asse principale dell'iperbole, quello che passa attraverso i fuochi F1 e F2, coincide con l'asse delle ascisse x o con l'asse delle ordinate y.
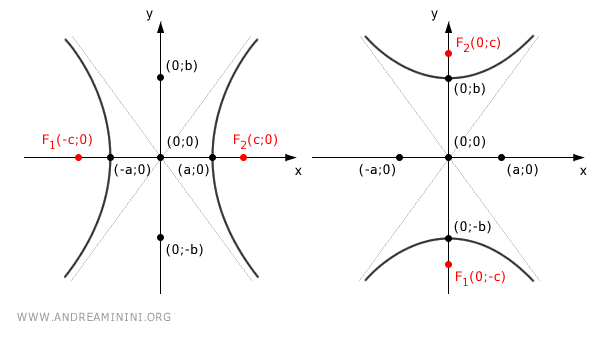
Questa semplificazione mi permette di usare l'equazione canonica dell'iperbole.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$
Dove "a" e "b" sono le semidistanze tra i vertici dell'iperbole.
- Se l'asse principale è l'asse x, il termine noto dell'equazione canonica è +1 $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
- Se l'asse principale è l'asse y, il termine noto dell'equazione canonica è -1 $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
In altre parole, a seconda se i fuochi F1 e F2 si trovino sull'asse delle ascisse (x) o delle ordinate (y), il termine noto dell'equazione canonica dell'iperbole è +1 oppure -1.
In alternativa, posso usare anche l'equazione dell'iperbole in forma esplicita.
$$ y = \pm \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}-1 ) } \ \ \ \ \text{fuochi sull'asse x}$$
$$ y = \pm \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}+1 ) } \ \ \ \ \text{fuochi sull'asse y}$$
In base alla scelta dell'asse principale, i fuochi dell'iperbole sono situati nelle seguenti coordinate:
- Se l'asse principale è l'asse x $$ F_1(-c;0 ) $$ $$ F_2(c;0 ) $$
- Se l'asse principale è l'asse y $$ F_1(0;-c ) $$ $$ F_2(0;c ) $$
Dove "c" è la distanza dei fuochi dal centro dell'iperbole.
$$ c = \sqrt{a^2+b^2} $$
Nota. Se l'asse principale è l'asse x, il valore "c" è sempre maggiore di "a" (c>a). Viceversa, se l'asse principale è l'asse y, il valore "c" è sempre maggiore di "b" (c>b).
Gli asintoti dell'iperbole sono le rette individuate dalle seguenti equazioni
$$ y = \pm \frac{b}{a} x $$
In questo caso semplificato gli asintoti dell'iperbole passano sempre per l'origine O(0;0) degli assi cartesiani e, rispettivamente, per il punto (a;b) o il punto (a;-b).
Infine, l'eccentricità (e) dell'iperbole si misura tramite il rapporto tra la distanza dei fuochi (c) e dei vertici reali (a) dal centro.
$$ e = \frac{c}{a} $$
Quanto più è alto il valore "e" tanto più i rami dell'iperbole sono aperti.
Nota. A differenza dell'ellisse, nel caso dell'iperbole l'eccentricità è sempre un valore maggiore di 1 ossia e>1 perché la distanza dei fuochi dal centro è sempre maggiore della distanza dei vertici.
Ogni iperbole ha due fuochi e due rette direttrici simmetriche e perpendicolari all'asse trasverso.
Se l'asse trasverso è l'asse x, le rette direttrici sono le seguenti:
$$ x = \pm \frac{a^2}{c} $$
Se l'asse trasverso è l'asse y, le rette direttrici sono:
$$ y = \pm \frac{b^2}{c} $$
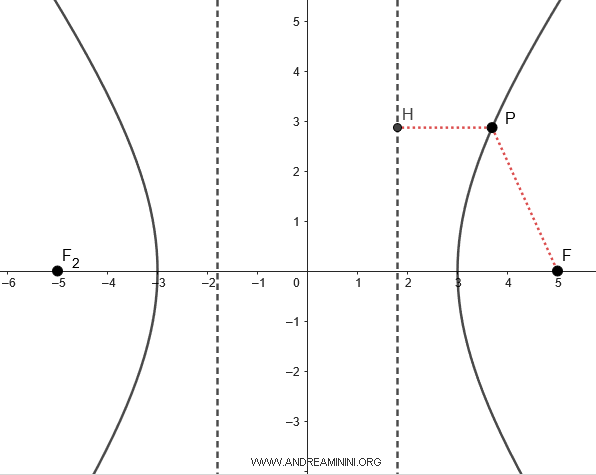
In generale, come per ogni conica, dato un punto $ P(x;y) $ dell'iperbole, il rapporto tra la distanza $ \overline{PF} $ del punto dal fuoco e quella $ \overline{PH} $ del punto dalla direttrice è costante, ed è uguale all'eccentricità (e).
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
Un esempio pratico
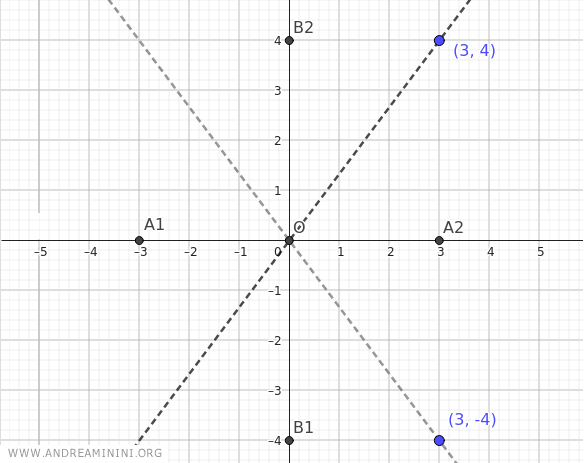
Considero un iperbole con i fuochi nell'asse x, il centro nell'origine degli assi cartesiani O(0;0) e con a=3 e b=4
Per prima cosa individuo i punti (a;b)=(3;4) e (a;-b)=(3;-4)
Poi traccio le rette passanti per il centro dell'iperbole e per i due punti (3;4) e (3;-4).
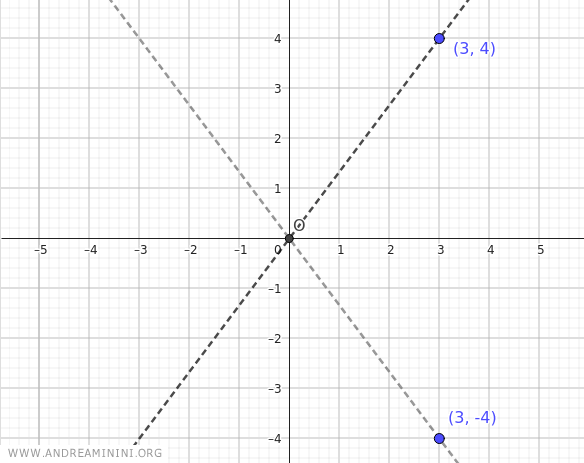
In questo modo ottengo gli asintoti dell'iperbole.
Per trovare gli asintoti avrei potuto anche utilizzare l'equazione in forma esplicita.
$$ y = \pm \frac{b}{a} \cdot x $$
Sostituisco a=3 e b=4
$$ y = \pm \frac{4}{3} \cdot x $$
Una volta tracciati gli asintoti, trovo i vertici dell'iperbole.
In questo caso i fuochi si trovano sull'asse x, quindi i vertici reali dell'iperbole sono A1(-a;0) e A2(a;0) e quelli non reali B1(0;-b) e B2(0;b)
Sapendo che a=3 e b=4 i vertici reali si trovano alle coordinate A1(-3;0) e A2(3;0) mentre i vertici non reali alle coordinate B1(0;-4) e B2(0;4)
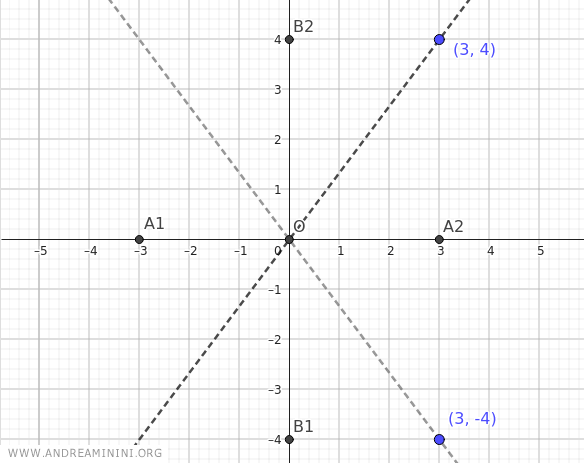
A questo punto devo calcolare le coordinate (x;y) dei fuochi dell'iperbole.
I fuochi si trovano alla distanza "c" dal centro dell'iperbole che trovo usando questa formula
$$ c = \sqrt{a^2+b^2} $$
Sostituisco a=3 e b=4
$$ c = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5 $$
Poiché l'asse principale è l'asse x, i fuochi si trovano alle seguenti coordinate F1(-c;0) e F2(c;0) dove c=5
$$ F_1(-5;0) $$
$$ F_2(5;0) $$
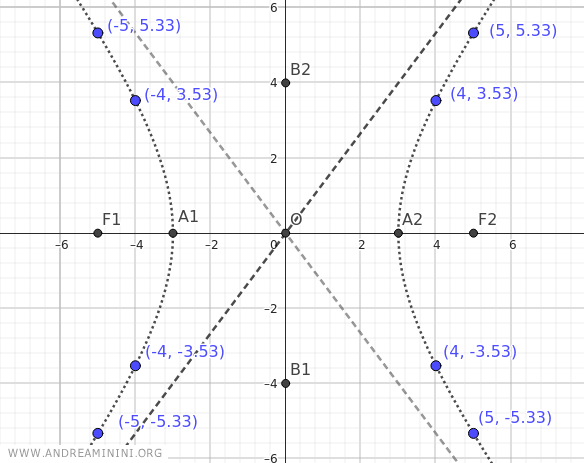
Aggiungo i due fuochi F1(-5;0) e F2(5;0) al piano cartesiano.
Infine, posso trovare gli altri punti dell'iperbole usando l'equazione canonica dell'iperbole.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
In questo caso il termine noto dell'equazione è +1 perché i fuochi dell'iperbole si trovano sull'asse x.
Ricavo y in funzione di tutto il resto.
$$ - \frac{y^2}{b^2} = 1 - \frac{x^2}{a^2} $$
$$ - y^2 = b^2 \cdot ( 1 - \frac{x^2}{a^2}) $$
Moltiplico entrambi i membri dell'equazione per -1 per avere il segno positivo della y
$$ - y^2 \cdot (-1) = b^2 \cdot ( 1 - \frac{x^2}{a^2}) \cdot (-1) $$
$$ y^2 = - b^2 \cdot ( 1 - \frac{x^2}{a^2}) $$
$$ y^2 = b^2 \cdot ( \frac{x^2}{a^2}-1) $$
Per la proprietà invariantiva calcolo la radice quadrata in entrambi i membri dell'equazione
$$ \sqrt{ y^2 } = \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}-1) } $$
$$ y = \pm \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}-1 ) } $$
Sostituisco i parametri a=3 e b=4 dell'iperbole.
$$ y = \pm \sqrt{ 4^2 \cdot ( \frac{x^2}{3^2}-1 ) } $$
$$ y = \pm \sqrt{ 16 \cdot ( \frac{x^2}{9}-1 ) } $$
In questo modo posso trovare la componente y di ogni punto (x;y) a partire dalla componente "x" nell'intervallo (-∞,-a]∪[a,∞) ossia (-∞,-3]∪[3,∞).
| x | y |
|---|---|
| -5 | ±5.33 |
| -4 | ±3.53 |
| -3 | 0 |
| 3 | 0 |
| 4 | ±3.53 |
| 5 | ±5.33 |
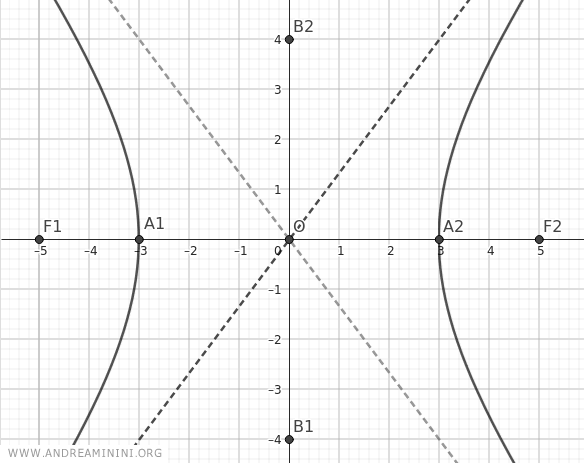
Questi sono i punti appena trovati che già danno l'idea approssimativa della forma dell'iperbole.
Per rendere il grafico più preciso non resta altro da fare che calcolare le coordinate degli altri punti.
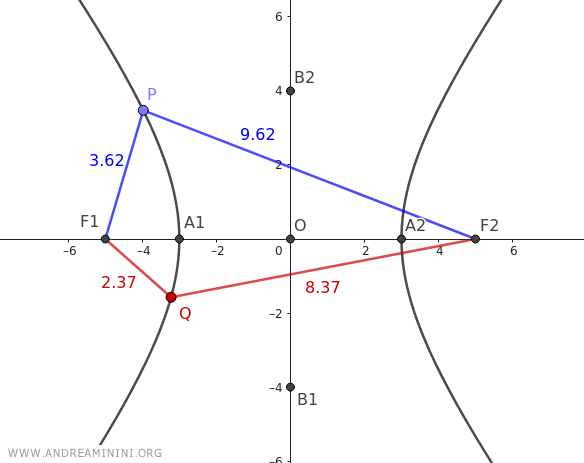
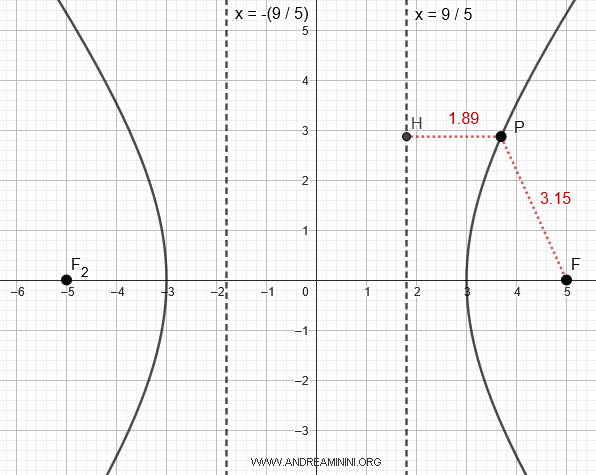
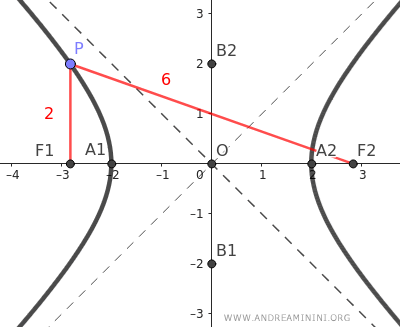
Nota. Come già detto l'iperbole è il luogo geometrico in cui ogni punto ha la stessa differenza delle distanze tra i fuochi in valore assoluto. Arrivato a questo punto posso verificare questa proprietà. Considero due punti P e Q dell'iperbole e calcolo le rispettive distanze dai fuochi. Il punto P (blu) dista 3.62 da F1 e 9.62 da F2. Quindi, la differenza assoluta delle distanze è |9.62-3.62|=6. Il punto Q (rosso) dista 2.37 da F1 e 8.37 da F2. Anche in questo caso la differenza assoluta delle distanze è uguale a 6 perché |8.37-2.37|=6. Lo stesso vale per qualsiasi altro punto dell'iperbole.
L'iperbole ha l'asse trasverso concidente con l'asse x, quindi le rette direttrici sono:
$$ x = \pm \frac{a^2}{c} = \pm \frac{9}{5} $$
Il rapporto tra la distanza $ \overline{PF} $ di un punto $ P(x;y) $ e il fuoco $ F(c,0) $ dell'iperbole e la distanza $ \overline{PH} $ dello stesso punto $ P $ rispetto alla retta direttrice è costante ed è uguale all'eccentricità (e) dell'iperbole.
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
Ad esempio, nel caso particolare del punto $ P $ i segmenti sono lunghi $ \overline{PF} = 3.15 $ e \overline{PH} = 1.89 $
$$ e = \frac{ \overline{PF} }{ \overline{PH} } = \frac{3.15}{1.89} = 1.67 $$
Questo rapporto $ e=1.67 $ è costante per qualsiasi altro punto dell'iperbole.
Nota. Un altro modo per calcolare l'eccentricità dell'iperbole è la formula $$ e = \frac{c}{a} $$ In questo caso $ c=5 $ e $ a=3 $ $$ e = \frac{c}{a} = \frac{5}{3} = 1.67 $$ Il risultato finale è lo stesso.
Esempio 2
In questo esempio calcolo l'iperbole con i fuochi sull'asse delle ordinate y e il centro nell'origine degli assi cartesiani O(0;0), usando gli stessi parametri a=3 e b=4 dell'esercizio precedente.
Gli asintoti sono le rette che passano per l'origine e per i punti (a;b) o (a;-b) ossia (3;4) o (3;-4).

Come si può notare gli asintoti sono sempre gli stessi.
Anche i vertici dell'iperbole sono gli stessi ma, in questo caso, i vertici reali sono B1(0;-b) e B2(0;b) mentre quelli non reali sono A1(-a;0) e A2(a;0)
In altre parole, in questo caso la curva dell'iperbole passa per i punti B1 e B2.
Sapendo che a=3 e b=4, i vertici reali si trovano alle coordinate B1(0;-4) e B2(0;4) mentre i vertici non reali alle coordinate A1(-3;0) e A2(3;0)

I fuochi dell'iperbole si trovano sempre alla distanza "c" dal centro dell'iperbole.
La formula per calcolare la distanza è sempre la stessa.
$$ c = \sqrt{a^2+b^2} $$
Sostituisco a=3 e b=4
$$ c = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5 $$
In questo caso, però, l'asse principale è l'asse y.
Quindi, le coordinate dei fuochi sono diverse dall'esercizio precedente. Sono F1(0;-c) e F2(0;c) con c=5
$$ F_1(0;-5) $$
$$ F_2(0;5) $$
Aggiungo i due fuochi F1(0;-5) e F2(0;5) nel grafico.
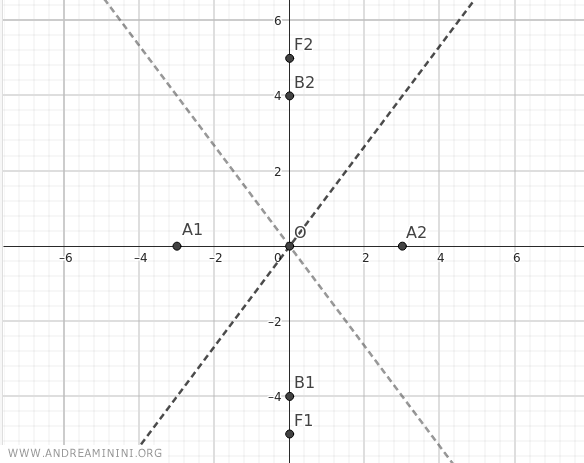
A questo punto posso cercare i vari punti dell'iperbole usando l'equazione canonica dell'iperbole.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
In questo caso il termine noto dell'equazione è -1 perché i fuochi dell'iperbole si trovano sull'asse y.
Ricavo y in funzione di tutto il resto.
$$ y = \pm \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}+1 ) } $$
Sostituisco a=3 e b=4
$$ y = \pm \sqrt{ 4^2 \cdot ( \frac{x^2}{3^2}+1 ) } $$
$$ y = \pm \sqrt{ 16 \cdot ( \frac{x^2}{9}+1 ) } $$
Poi la utilizzo per trovare le coordinate (x;y) di alcuni punti nell'intervallo (-∞,∞).
| x | y |
|---|---|
| -2 | ±4.81 |
| -1 | ±4.22 |
| 0 | 0 |
| 1 | ±4.22 |
| 2 | ±4.81 |
| 3 | ±5.66 |
Queste prime coordinate (x;y) mi danno già l'idea della forma dell'iperbole.
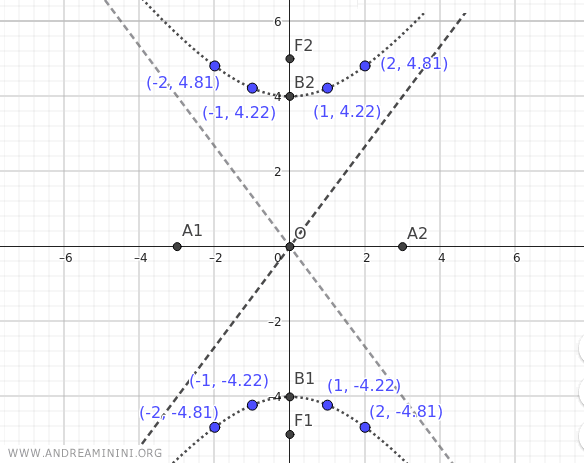
Il risultato finale è una iperbole con i fuochi sull'asse y.
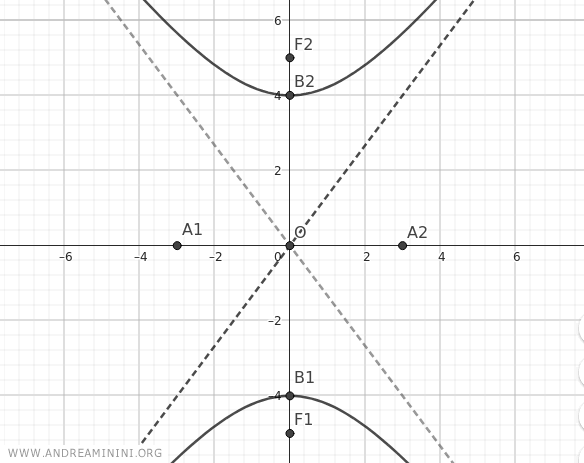
In questo caso l'asso trasverso, quello in cui si trovano i fuochi, coincide con l'asse y.
Quindi, le rette direttrici sono perpendicolari all'asse y.
$$ y = \pm \frac{b^2}{c} = \frac{16}{5} = 3.2 $$
Anche in questo caos il rapporto tra le distanze $ \overline{PF} $ e $ \overline{PH} $ è costante ed è uguale all'eccentricità (e) dell'iperbole.
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
Ad esempio, nel caso particolare del punto $ P $ i segmenti sono lunghi $ \overline{PF} = 3.69 $ e \overline{PH} = 2.95 $
$$ e = \frac{ \overline{PF} }{ \overline{PH} } = \frac{3.69}{2.95} = 1.25 $$
Il rapporto $ e=1.25 $ è l'eccentricità dell'iperbole ed è costante per qualsiasi altro punto dell'iperbole.
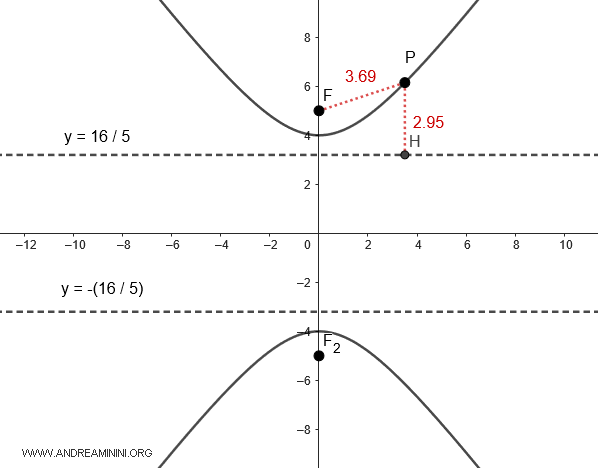
Nota. Un altro modo per calcolare l'eccentricità dell'iperbole con l'asse focale sull'asse y è la seguente formula $$ e = \frac{c}{b} = \frac{5}{4} = 1.25 $$ Il risultato finale è sempre lo stesso.
Osservazioni
Alcune osservazioni e note a margine sull'iperbole
- Iperbole equilatera
L'iperbole equilatera è un caso particolare di iperbole in cui a=b. Nell'iperbole equilatera i vertici reali sull'asse trasverso (A1, A2) e quelli non reali sull'asse non trasverso (B1,B2) hanno la stessa distanza dal centro dell'iperbole.
- Una retta interseca l'iperbole in non più di due punti reali
- Se la retta interseca l'iperbole in due punti distinti è detta retta secante all'iperbole.
- Se la retta interseca l'iperbole in un solo punto è detta retta tangente all'iperbole.
Nota. In un punto P' qualsiasi del piano possono passare al massimo due rette tangenti all'iperbole. In un punto P dell'iperbole, invece, passa una sola retta tangente.
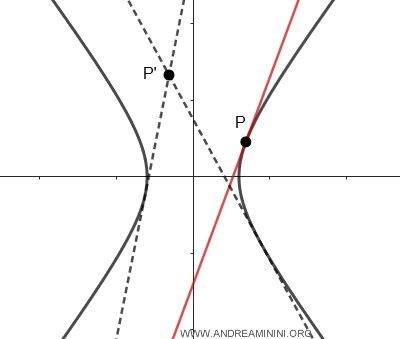
- Quando una retta non interseca l'iperbole in nessun punto, è detta retta esterna all'iperbole.
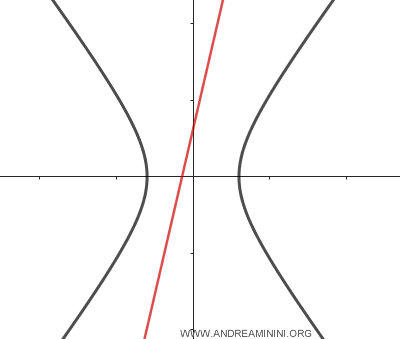
- Se la retta interseca l'iperbole in due punti distinti è detta retta secante all'iperbole.
- Proprietà focale dell'iperbole
In una iperbole se traccio una tangente (t) all'iperbole in un punto \( P \) sulla curva, la perpendicolare (n) a questa tangente nel punto \( P \) divide l'angolo formato dal raggio focale \( PF_1 \) e il prolungamento del raggio focale \( PF_2 \) in due angoli congruenti $ \alpha \cong \beta $.
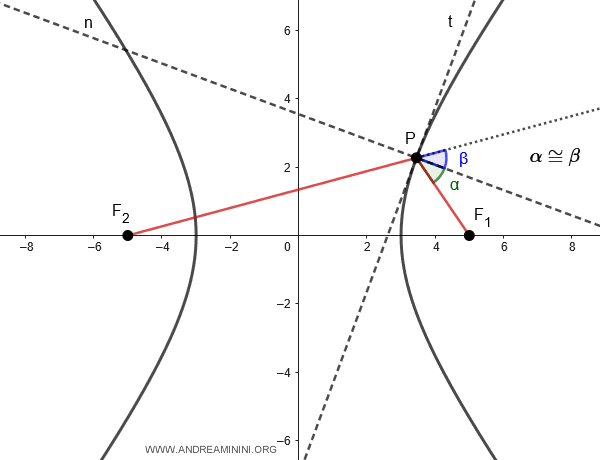
Questo significa che se un fuoco è la sorgente di un raggio luminoso (ad esempio F1 ), questo viene riflesso dallo specchio iperbolico come se provenisse dall'altro fuoco (es. F2 ).
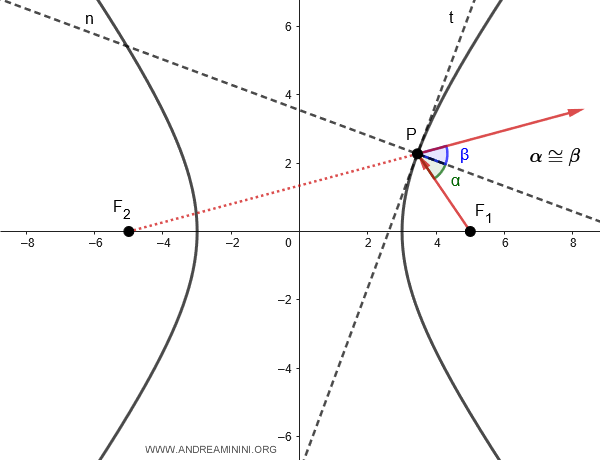
E così via.
