Cono
Il cono è un solido ottenuto tramite la rotazione completa di un triangolo rettangolo ABC attorno a uno dei suoi cateti, preso come asse di rotazione.
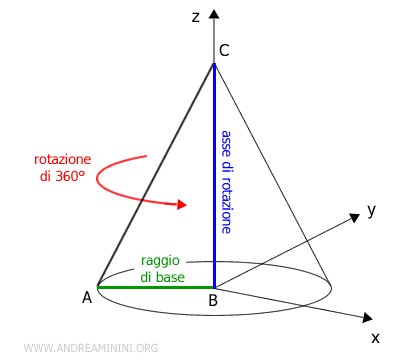
Il cateto scelto come asse di rotazione definisce l'altezza del cono.
L'altro cateto è il raggio di base del cono, mentre l'ipotenusa è l'apotema del cono.
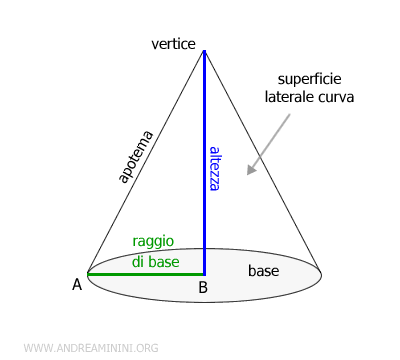
Il cono è composto da una base circolare e da una superficie laterale curva.
L'estremo dell'altezza opposto alla base è detto vertice del cono.
Il cono è uno dei solidi di rotazione più conosciuti, insieme alla sfera e al cilindro.
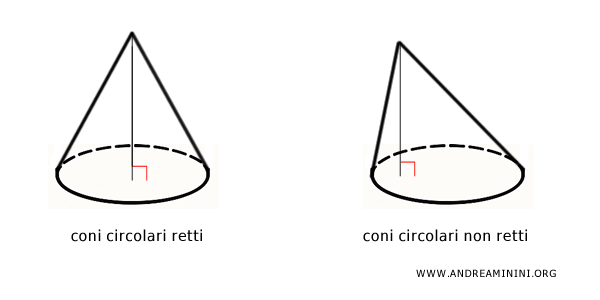
Nella geometria elementare quando si parla di cono si intende il cono finito circolare retto che ha una base circolare completa e un'altezza perpendicolare. Più in generale, esistono anche altre tipologie di coni, detti coni indefiniti, come il cono ellittico, con circolare non retto, cono quadratico, ecc. Pertanto, il cono circolare retto è solo uno dei molti tipi di coni possibili. Ci sono coni indefiniti che non sono ottenibili tramite una semplice rotazione completa di un triangolo. Ad esempio, nel cono non retto l'altezza non coincide con l'asse di rotazione.
Le formule
Alcune formule utili per il calcolo delle metriche di un cono circolare retto
La superficie laterale è il prodotto tra la semicirconferenza di base \( \pi r \) e l'apotema.
$$ S_L = \pi r \cdot a $$
Dove "r" è il raggio di base e "a" è l'apotema del cono.

La superficie della base
La base di un cono circolare retto è un cerchio, quindi la superficie della base è semplicemente la superficie di un cerchio di raggio "r"
$$ S_B = \pi r^2 $$
La superficie totale
La superficie totale del cono è uguale alla somma della superficie laterale e della superficie della base del cono.
$$ S_T = S_L + S_B $$
$$ S_T = \pi r \cdot a + \pi r^2 $$
$$ S_T = \pi r \cdot ( a + r) $$
Dove "r" è il raggio di base e "a" è l'apotema.
Il volume del cono
Il volume del cono è 1/3 di un cilindro circolare retto che ha la stessa base e la stessa altezza.
$$ V = \frac{1}{3} \pi r^2 \cdot h $$
Dove "r" è il raggio di base e "h" è l'altezza.
Nota. In base al teorema di equivalenza del volume di un cono e una piramide, posso scrivere $$ V = \frac{1}{3} \cdot A \cdot h = \frac{1}{3} \pi r^2 h $$
Tipi di cono
I coni possono essere classificati in diverse categorie basate su varie caratteristiche geometriche. Ecco alcuni tipi principali di coni:
- Cono circolare retto
È il tipo più comune di cono, caratterizzato da una base circolare e un'altezza che va dal vertice al centro della base. In questo cono, l'asse è perpendicolare alla base. - Cono circolare obliquo
E' simile al cono circolare retto perché ha una base circolare ma con l'asse inclinato rispetto alla base. Quindi, il vertice che non è direttamente sopra il centro della base. - Cono ellittico
Ha una base ellittica anziché circolare. L'asse può essere perpendicolare o obliquo rispetto alla base. - Cono parabolico
E' un solido di rotazione formato dalla rotazione di una parabola attorno al suo asse. Non ha una base circolare definita come nei coni circolari. - Cono iperbolico
È formato dalla rotazione di un'iperbole attorno al suo asse. Questo cono ha due parti separate e simmetriche. - Cono sferico
E' un solido che si ottiene dalla rotazione di un semicerchio attorno al suo diametro, che è anche l'altezza del cono. Ha una base circolare e una superficie curva che si unisce al vertice, simile a una calotta sferica.
Questi sono solo alcuni esempi dei tipi di coni che si possono incontrare in geometria.
Il cono nella geometria analitica
Nella geometria analitica, il cono è un tipo di superficie quadrica che può essere rappresentato attraverso un'equazione in coordinate cartesiane.
Equazione generale del cono
Questa equazione generale può rappresentare diversi tipi di coni, inclusi quelli non circolari, a seconda dei valori di a, b, e c.
$$ \begin{pmatrix} \frac{x}{a} \end{pmatrix} ^2 + \begin{pmatrix} \frac{y}{b} \end{pmatrix} ^2 - \begin{pmatrix} \frac{z}{c} \end{pmatrix} ^2 = 0 $$
Dove x, y, z sono le coordinate dei punti (x;y;z) in uno spazio cartesiano a tre dimensioni.
Equazione del cono circolare retto
La forma più comune di un cono nella geometria analitica è quella del cono circolare retto, la cui equazione standard è la seguente:
$$ x^2 + y^2 = z^2 \cdot \begin{pmatrix} \frac{r}{h} \end{pmatrix}^2 $$
Dove r è il raggio della base del cono e h è l'altezza del cono. Il rapporto r/h determina la pendenza della superficie del cono.
Questa equazione rappresenta un cono con il vertice nell'origine (x;y;z)=(0;0;0) del piano cartesiano, l'asse di rotazione lungo l'asse z e una base circolare nel piano xy.
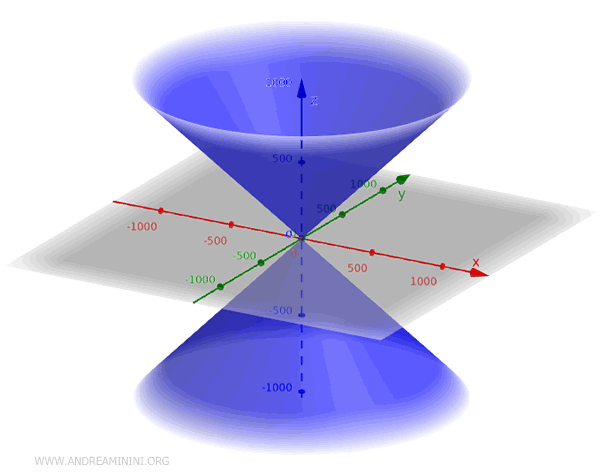
L'equazione standard di solito rappresenta un cono doppio che si estende sia sopra sia sotto il piano xy.
Quindi, per limitare il cono a una sola di queste regioni, devo imporre delle restrizioni aggiuntive sull'equazione.
Ad esempio, un piano parallelo a xy che interseca il cono a una determinata altezza e la condizione z>0.
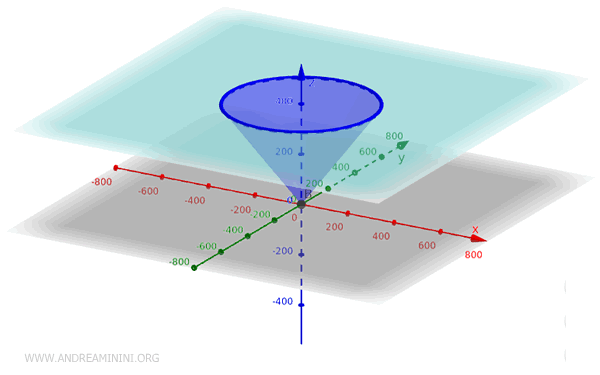
Nota. Le equazioni di un cono possono variare a seconda della sua orientazione e posizione nello spazio. Ad esempio, modificando l'equazione standard, posso ottenere coni con vertici in punti diversi dall'origine o con assi allineati lungo gli assi x o y.
La superficie conica circolare retta
L'equazione di una superficie con il vertice nell'origine $ O $ degli assi cartesiani, l'asse coincidente con l'asse z e una semiapertura $ \delta $ è $$ x^2 + y^2 - k^2 z^2 = 0 $$ dove $ k^2 = \tan^2 \delta $
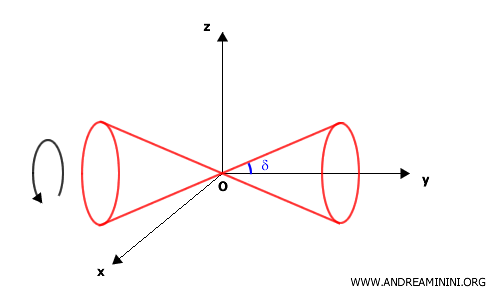
Se l'asse della superficie conica coincide con l'asse x, l'equazione diventa:
$$ y^2 + z^2 - k^2 x^2 = 0 $$
Se l'asse della superficie conica coincide con l'asse y, invece, l'equazione diventa:
$$ x^2 + z^2 - k^2 y^2 = 0 $$
Sempre con $ k^2 = \tan^2 \delta $.
Dimostrazione
Considero una retta $ r $ passante per l'origine degli assi cartesiani $ O $ che forma un angolo $ \delta $ rispetto all'asse $ y $
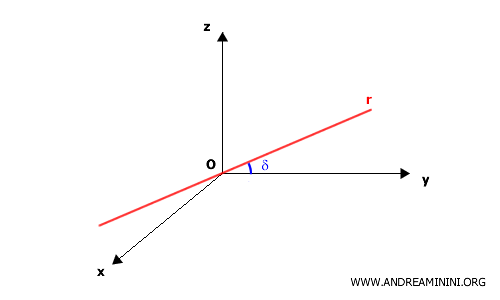
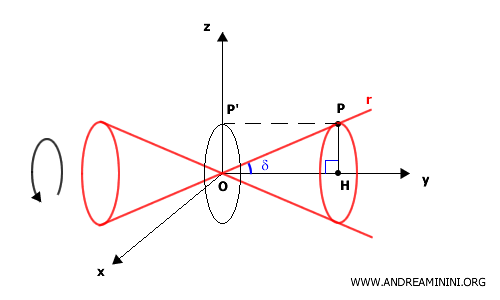
Questa retta è detta generatrice del cono, poiché la sua rotazione attorno all'asse $y$ genera la superficie conica.
Prendo un punto $ P(x,y,z) $ sulla retta $ r $ e la sua proiezione ortogonale $ H $ sull'asse $ y $.
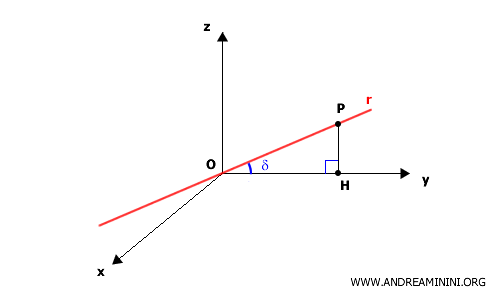
Il triangolo $ OPH $ è un triangolo rettangolo con un angolo acuto pari a $ \delta $.
Se considero l'ipotenusa $OP$, il cateto $OH$ corrisponde alla proiezione di $OP$ sull'asse $y$ e vale:
$$ OH = |OP| \cdot \cos \delta $$
Il segmento $PH$ invece è il cateto opposto all'angolo $\delta$ e rappresenta:
$$ PH = |OP| \cdot \sin \delta $$
In particolare, se prendo $|OP|=1$, risulta:
$$ OH = \cos \delta $$
$$ PH = \sin \delta $$
Di conseguenza, la tangente dell'angolo $ \delta $ è
$$ \tan \delta = \frac{ \sin \delta }{ \cos \delta } = \frac{PH}{OH} $$
Sapendo che il segmento $ OH $ ha una lunghezza $ OH = |y| $
$$ \tan \delta = \frac{PH}{|y|} $$
Il segmento $ PH $ è il raggio di una circonferenza, la cui proiezione sul piano $ xz $ ha come centro l'origine $ O $ e raggio $ OP' $. L'equazione di questa circonferenza è $ x^2 + z^2 = OP'^2 $
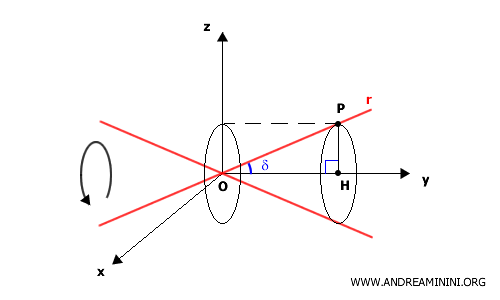
Poiché $ OP' = PH $ posso scrivere la circonferenza come $ x^2 + z^2 = PH^2 $ da cui ricavo $ PH = \sqrt{x^2+z^2} $
Quindi, sostituisco $ PH = \sqrt{x^2+z^2} $ nell'equazione $ \tan \delta = \frac{PH}{|y|} $.
$$ \tan \delta = \frac{\sqrt{ x^2+z^2} }{|y|} $$
Elevo al quadrato entrambi i membri dell'equazione e semplifico.
$$ (\tan \delta )^2 = \left( \frac{\sqrt{ x^2+z^2} }{|y|} \right)^2 $$
$$ \tan^2 \delta = \frac{x^2+z^2}{y^2} $$
$$ y^2 \tan^2 \delta = x^2+z^2 $$
$$ x^2+z^2 - y^2 \tan^2 \delta = 0 $$
Ponendo $ k^2 = \tan^2 \delta $, l'equazione diventa
$$ x^2+z^2 - k^2 y^2 = 0 $$
Questo dimostra l'equazione della superficie conica con semiapertura $ \delta $ rispetto all'asse $ y $
Osservazioni
Alcune osservazioni sul cono.
- Cono equilatero
Un cono è detto cono equilatero quando l'apotema (a) è congruente al diametro d=2r della base del cono. $$ a = 2r $$ Dove "r" è il raggio di base del cono. L'intersezione tra un cono equilatero e un piano che contiene l'altezza del cono è un triangolo equilatero. - Cono troncato
Un cono troncato (o tronco di cono) è un solido ottenuto tagliando un cono con un piano parallelo alla sua base, rimuovendo così la parte superiore. Questo solido ha due basi circolari di diametri diversi, una più grande (la base del cono originale) e una più piccola (la sezione del taglio). - Sezioni coniche
Le intersezioni di un cono con piani possono produrre varie sezioni coniche, come ellissi, parabole e iperboli, a seconda dell'angolo e della posizione del piano di taglio.
E così via.
