Legge di conservazione della quantità di moto
La legge di conservazione della quantità di moto dice che in un sistema isolato (cioè senza forze esterne) la quantità di moto totale $ \vec{P} $ resta costante. $$ \vec{P} = \sum_i m_i \vec{v}_i $$Dove $m$ è la massa della particella e $\vec{v}$ è la velocità.
La quantità di moto è una grandezza che combina massa e velocità:
$$ \vec{p} = m \vec{v} $$
Questa grandezza mi permette di valutare l'influenza di un corpo in movimento quando interagisce con altri corpi, considerando sia la sua massa che la sua velocità.
Ad esempio, un camion ha una massa grande, quindi anche se cammina lento ha tanta quantità di moto. Viceversa, una pallina da ping-pong è leggera e anche se va veloce, ne ha poca.
Secondo la legge di conservazione della quantità di moto, se non c’è una forza esterna che spinge o tira l’intero sistema, la somma delle quantità di moto iniziale e finale di un processo rimane identica.
$$ \vec{P}_{\text{iniziale}} = \vec{P}_{\text{finale}} $$
Quindi, la quantità di moto è una grandezza invariante. Questo però vale solo se il sistema è chiuso e isolato.
Un esempio semplice
Considero due pattinatori su ghiaccio liscio con l'attrito trascurabile.
All’inizio stanno entrambi fermi, la quantità di moto totale è zero. Quando si spingono: uno scivola a destra, l’altro a sinistra.

Il risultato è che la quantità di moto del primo è uguale e opposta a quella del secondo. Quindi, la somma resta zero, come all’inizio.
In altre parole, se la risultante delle forze esterne è nulla ($\vec{F}_{\text{est}}=0$), allora
$$ \frac{d\vec{P}}{dt} = 0 \quad \Rightarrow \quad \vec{P}_{\text{iniziale}} = \vec{P}_{\text{finale}} $$
Esempio 2
Considero due palle da biliardo, ognuna pesa 200 grammi, che si muovono con velocità differenti.
- Palla A: massa $m_A = 0.2 \,\text{kg}$, velocità iniziale $v_A = 5 \,\text{m/s}$.
- Palla B: massa $m_B = 0.2 \,\text{kg}$, inizialmente ferma ($v_B = 0$).
La palla B è ferma mentre la palla A si sposta con una velocità di 5 metri al secondo.
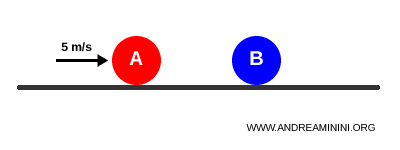
Prima dell’urto la quantità di moto totale del sistema è 1 kg per m/s
$$ p_{\text{tot}} = m_A v_A + m_B v_B = 0.2 \cdot 5 + 0.2 \cdot 0 = 1.0 \,\text{kg·m/s} $$
A un certo punto la palla A urta frontalmente contro la palla B.
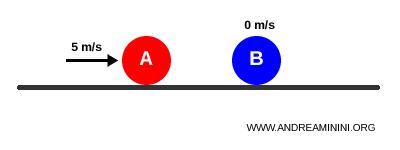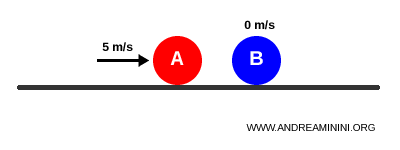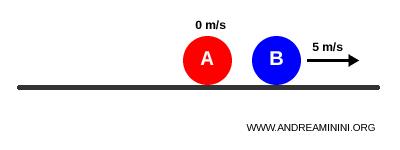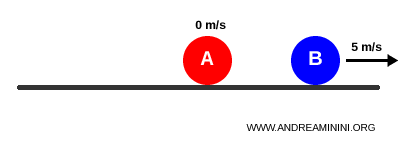
Dopo l’urto elastico, la palla A si ferma mentre la palla B prende tutta la velocità.
$$ v_A' = 0 $$
$$v_B' = 5 \,\text{m/s} $$
La quantità di moto del sistema è rimasta costante.
$$ p_{\text{tot, finale}} = m_A v_A + m_B v_B = 0.2 \cdot 0 + 0.2 \cdot 5 = 1.0 $$
Quindi negli urti, sia elastici che anelastici, la quantità di moto totale si conserva.
Esempio 3
Considero un fucile di una massa $m_f = 4 \,\text{kg}$ e un proiettile di massa $m_p = 0.02 \,\text{kg}$
Il fucile è inizialmente fermo e la quantità di moto totale è nulla.
$$ p_{\text{iniziale}} = 0 $$
Quando il fucile spara, il proiettile esce a una velocità di $v_p = 400 \,\text{m/s}$
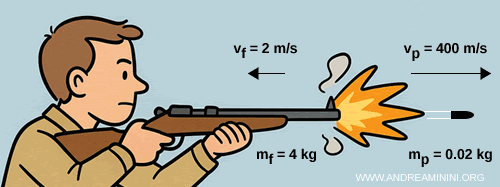
La quantità di moto del proiettile è:
$$ p_p = m_p \cdot v_p = 0.02 \cdot 400 = 8 \,\text{kg·m/s} $$
Per la conservazione della quantità di moto, il fucile deve avere quantità di moto uguale e opposta:
$$ p_f = -8 \,\text{kg·m/s} $$
Questo vuole dire che, per compensare, il fucile si sposta in direzione opposta con una velocità di 2 m/s.
$$ v_f = \frac{p_f}{m_f} = \frac{-8}{4} = -2 \,\text{m/s} $$
Questo spiega il rinculo del fucile dopo lo sparo.
Complessivamente, la quantità di moto totale resta zero:
$$ p_{\text{tot}} = p_p + p_f = 8 - 8 = 0 $$
Ma c’è una redistribuzione, il proiettile ottiene tanta velocità perché è leggero, il fucile poca velocità perché è molto più pesante.
Origine teorica
La legge di conservazione della quantità di moto deriva da un principio più profondo: la simmetria dello spazio.
Lo spazio è detto omogeneo se le leggi della fisica sono identiche in ogni punto.
In altre parole, spostare un sistema fisico di qualche metro a destra o a sinistra non modifica le equazioni che ne descrivono il moto.
Il teorema di Noether stabilisce che a ogni simmetria continua del sistema fisico corrisponde una grandezza conservata.
- Simmetria rispetto al tempo
L'invarianza per traslazioni temporali implica che l'energia si conserva. - Simmetria rispetto allo spazio
L'invarianza per traslazioni spaziali implica che la quantità di moto si conserva. - Simmetria rispetto alle rotazioni
L'invarianza per rotazioni spaziali implica che il momento angolare si conserva.
Pertanto, nel caso della traslazione spaziale la quantità di moto resta costante.
E così via.
