Teoremi delle sezioni parallele di un diedro
In un diedro le sezioni parallele sono congruenti.
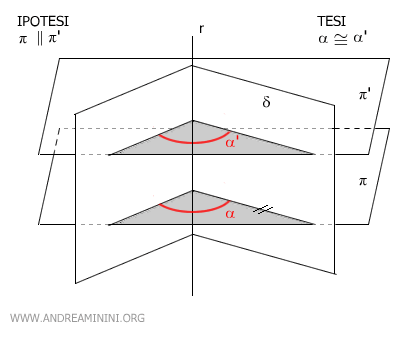
Ad esempio, il piano π interseca il diedro con un angolo diedrale α.
Il piano π' è parallelo al piano π (ossia π||π') e interseca il diedro con un angolo congruente α≅α'.
L'angolo diedrale è lo stesso, quindi, le due sezioni parallele sono congruenti.
La dimostrazione
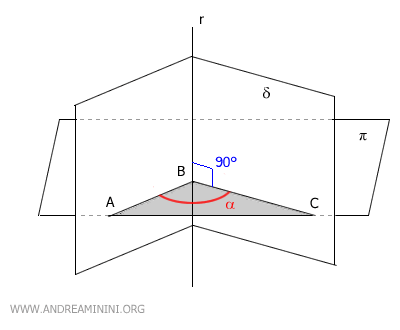
Considero il diedro δ e un piano π allo spigolo r del diedro (sezione normale).
Per semplicità espositiva utilizzo un piano perpendicolare (90°) ma qualsiasi altra inclinazione del piano andrebbe bene.
Il piano π interseca il diedro δ nei punti A, B, C.
Ora considero un piano parallelo π' parallelo al piano π.
Il piano π' interseca il diedro nei punti A', B', C'.
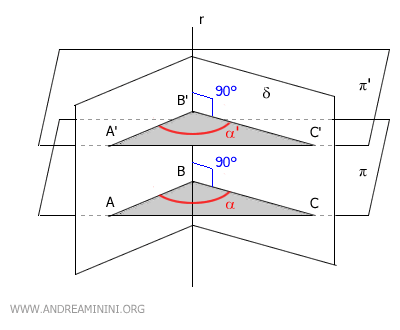
Essendo due piani paralleli, le figure AA'B'B e BB'C'C sono due parallelogrammi.
Sapendo che ogni parallelogramma ha i lati opposti congruenti, deduco che AA'≅BB', AB≅A'B', BB'≅CC' e BC≅B'C'.
Inoltre, per la proprietà transitiva se AA'≅BB' e BB'≅CC' allora AA'≅CC'
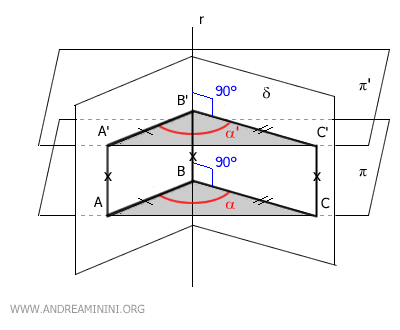
Una volta constatato che i lati AA'≅CC' sono congruenti, deduco che anche AA'C'C è un parallelogramma.
Quindi, i lati obliqui del parallelogramma AC≅A'C' sono congruenti.
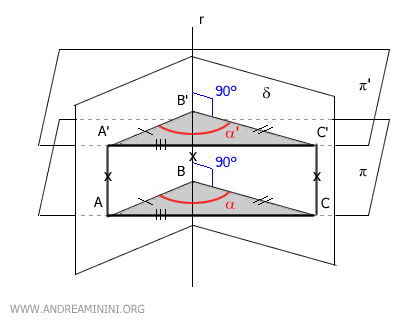
A questo punto mi basta osservare che i triangoli ABC e A'B'C' sono congruenti per il terzo criterio di congruenza (LLL), in quanto hanno tutti i lati congruenti AC≅A'C', AB≅A'B', BC≅B'C' .
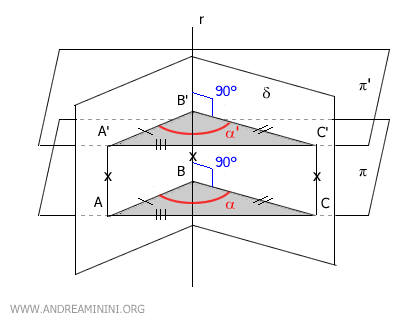
Essendo due triangoli congruenti, hanno tutti gli angoli congruenti nello stesso ordine.
In particolar modo, mi interessa sapere che sono congruenti gli angoli α≅ α', perché questo dimostra che le sezioni parallele del diedro δ sono congruenti.
$$ \alpha \cong \alpha ' $$
Il teorema è stato dimostrato.
E così via.
