Teorema di intersezione tra piani
Quando due piani distinti si intersecano nello spazio in un punto $ P $, condividono una retta $ r $ passante per quel punto.
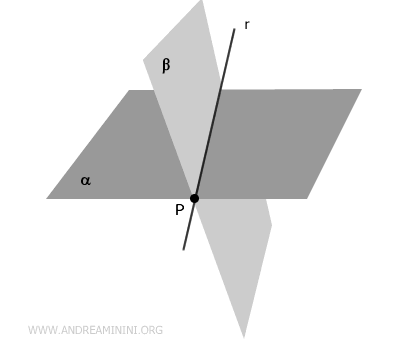
In altre parole, due piani incidenti non possono avere un solo punto in comune. Hanno in comune una retta.
La retta in comune tra i due piani è l'insieme di tutti i punti che appartengono contemporaneamente ai due piani.
Questo enunciato si basa su principi fondamentali della geometria dello spazio tridimensionale, in cui l'intersezione di due superfici piane nello spazio tridimensionale, se non sono parallele, genera una linea (retta).
Dimostrazione
Considero due piani \( \alpha \) e \( beta \) che si intersecano in un punto \( P \).
$$ P \in \alpha \cap \beta $$
Quindi, il punto \( P \) appartiene a entrambi i piani.

Prendo due punti qualsiasi $ A $ e $ B $ appartenenti allo stesso piano $ \alpha $ ma in regioni opposte rispetto al piano $ \beta $.
Traccio un segmento $ \overline{AB} $ che ha per estremi i punti $ A $ e $ B $.
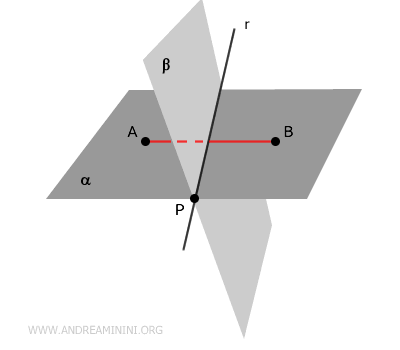
Poiché i due piani sono incidenti e il segmento $ \overline{AB} $ ha gli estremi in semipiani distinti del piano $ \alpha $, il segmento $ \overline{AB} $ deve necessariamente intersecare il piano $ \beta $ in un punto $ C $.
A questo punto ci sono due punti in comune tra i due piani, il punto $ P $ iniziale e il punto $ C $.
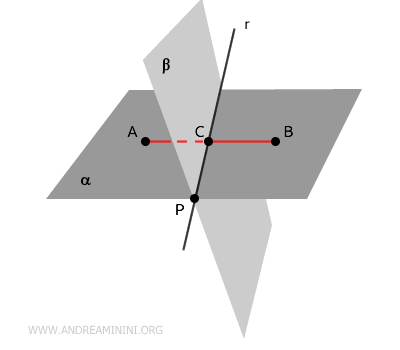
Tra due punti passa una e una sola retta $ r $ che ha la caratteristica di appartenere a entrambi i piani.
Ho così dimostrato che se due piani hanno un comune un punto \( P \), allora hanno in comune anche una retta \( r \) che passa per quel punto.
E così via.
