Il vettore direttore di una retta
Il vettore direttore determina l'inclinazione di una retta in un'equazione vettoriale. $$ \begin{pmatrix} x \\ y \end{pmatrix} = P_0 + t \cdot v_r $$
Nella precedente equazione vettoriale
- P0 è un punto qualsiasi della retta.
- t è il parametro dell'equazione parametrica vettoriale
- vr è il vettore direttore della retta
Un esempio pratico di vettore direttore
Il punto P0 appartiene alla retta r
$$ P_0 = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
La retta r ha il seguente vettore direttore
$$ v_r = \begin{pmatrix} l \\ m \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$
Quindi, l'equazione vettoriale della retta è
$$ \begin{pmatrix} x \\ y \end{pmatrix} = P_0 + t \cdot v_r $$
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$
Per rendere ancora più chiara la spiegazione rappresento la retta, il punto P e il vettore v_r sul diagramma cartesiano.
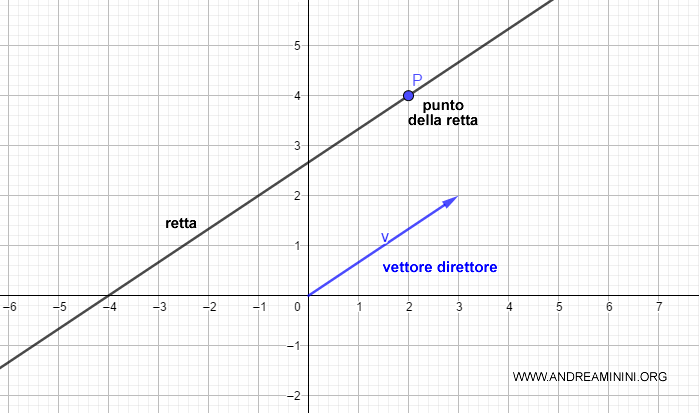
Il vettore direttore è sempre parallelo (o coincidente se la retta passa per l'origine) alla retta che determina.
Quindi, presi due punti qualsiasi P1 e P2 della retta
$$ P_1 = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} $$
$$ P_2 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} $$
posso affermare che la retta e il vettore direttore sono sempre linearmente dipendenti tra loro.
$$ det \begin{pmatrix} x_2 - x_1 & l \\ y_2 - y_1 & m \end{pmatrix} = 0$$
Nota. Se due vettori sono linearmente dipendenti, il determinante della matrice costruita con i vettori è nullo. In questo caso i due vettori sono paralleli, proporzionali o coincidenti.
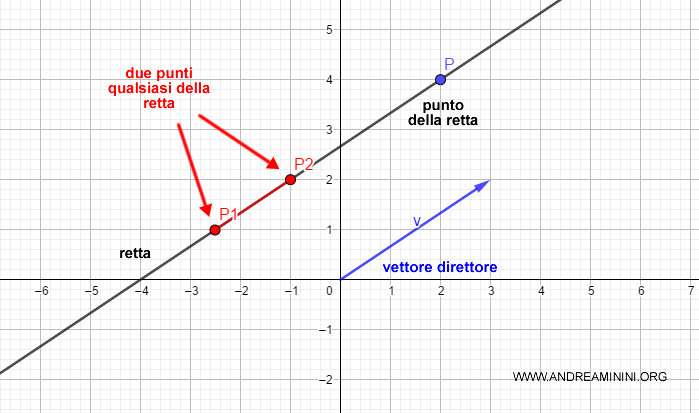
Guardando il diagramma cartesiano è subito evidente la dipendenza lineare.
Il segmento P2P1 ( rosso ) e il vettore direttore vr ( blu ) sono paralleli e proporzionali tra loro.
Come trovare il vettore direttore nelle equazioni cartesiane
Se la retta è rappresentata con un'equazione cartesiana
$$ a x + b y + c = 0 $$
Posso trovare il vettore direttore osservando il vettore normale della retta.
Il vettore normale n della retta è il vettore dei coefficienti.
$$ n = \begin{pmatrix} a \\ b \end{pmatrix} $$
So per certo dalla teoria che il vettore normale di qualsiasi retta è un vettore ortogonale (perpendicolare) al vettore direttore.
Due vettori sono ortogonali se il loro prodotto scalare è nullo.
$$ < v_1 , v_2 > = 0 $$
Pertanto, se il vettore v1 è il vettore normale n
$$ v_1 = n = \begin{pmatrix} a \\ b \end{pmatrix} $$
allora per avere un prodotto scalare nullo il vettore v2 deve essere necessariamente
$$ v_2 = \begin{pmatrix} -b \\ a \end{pmatrix} \:\:\:\: oppure \:\:\:\: v_2 = \begin{pmatrix} b \\ -a \end{pmatrix} $$
Infatti
$$ < \begin{pmatrix} a \\ b \end{pmatrix} , \begin{pmatrix} -b \\ a \end{pmatrix} > = ab - ab = 0 $$
$$ < \begin{pmatrix} a \\ b \end{pmatrix} , \begin{pmatrix} b \\ -a \end{pmatrix} > = ab - ab = 0 $$
Un esempio pratico
L'equazione cartesiana di una retta è
$$ 3x - 2y +4 = 0 $$
Il vettore normale n della retta è
$$ n = \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} 3 \\ -2 \end{pmatrix} $$
Il vettore ortogonale di n è il vettore direttore vr della retta.
$$ v_r \begin{pmatrix} -b \\ a \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$
Da un punto di vista geometrico, per ottenere il vettore direttore effettuo una rotazione di ±90° sul vettore normale.
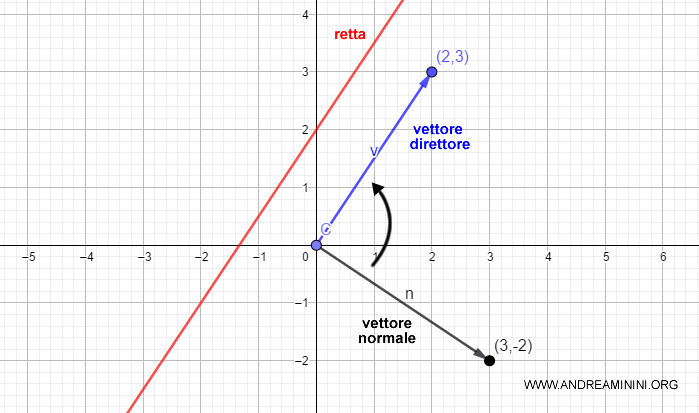
Una volta trovato il vettore direttore, mi basta trovare un punto qualsiasi P della retta per scrivere l'equazione parametrica o vettoriale della retta.
$$ \begin{pmatrix} x \\ y \end{pmatrix} = P + t \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$
Sapendo che l'equazione cartesiana della retta è
$$ 3x - 2y +4 = 0 $$
metto in evidenza la y
$$ y = \frac{4+3x}{2} $$
Quindi, se x=0
$$ y = \frac{4+3\cdot 0}{2} = \frac{4}{2} = 2 $$
Ho così trovato un punto della retta
$$ P = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \end{pmatrix} $$
Ora ho tutti gli elementi per scrivere l'equazione vettoriale della retta
$$ \begin{pmatrix} x \\ y \end{pmatrix} = P + t \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$
E una volta ottenuta l'equazione cartesiana è molto semplice passare all'equazione parametrica.
Basta trasformare i vettori in un sistema di equazioni.
$$ \begin{cases} x = 0 + 2t \\ y = 2 + 3t \end{cases} $$
E così via
