Area del parallelogramma
La formula per calcolare l'area di un parallelogramma è: $$ A = b \times h $$ dove \( A \) è l'area, \( b \) è la lunghezza della base, \( h \) è l'altezza, ossia la distanza perpendicolare tra la base e il lato opposto.
Il concetto di area di un parallelogrammo risale agli antichi matematici greci, come Euclide, che nel suo famoso libro "Elementi" descrive varie proprietà dei parallelogrammi e altre figure geometriche.
Un esempio pratico
Considero un parallelogramma con una base di 5 metri e un'altezza di 3 metri.
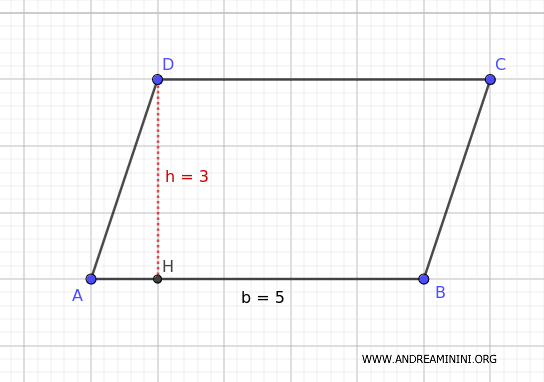
L'area del parallelogramma è
$$ A = 5 \, m \times 3 \, m = 15 \, m^2 $$
La spiegazione
Per comprendere come si arriva a questa formula, basta immaginare di trasformare il parallelogrammo in un rettangolo.
Traccio l'altezza interna del parallelogramma che passa per il vertice D.
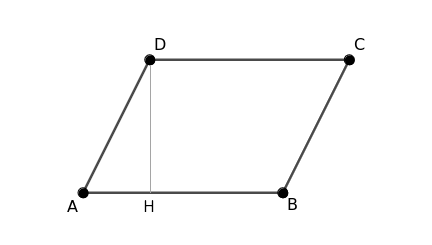
Taglio il triangolo ADH e lo sposto sull'altro lato.
In questo modo ottengo un rettangolo HDCE con la stessa base e altezza del parallelogrammo.
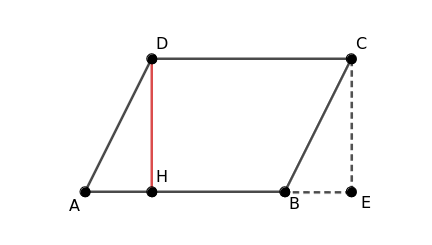
Quindi, un parallelogramma è equivalente a un rettangolo che ha la stessa base e la stessa altezza.
Poiché l'area del rettangolo è calcolata moltiplicando la base per l'altezza, lo stesso vale per il parallelogrammo.
Il calcolo dell'area con le coordinate cartesiane
Un metodo alternativo per trovare l'area di un parallelogrammo è usare le coordinate cartesiane dei vertici.
Se i vertici del parallelogrammo sono dati dai punti \( (x_1, y_1) \), \( (x_2, y_2) \), \( (x_3, y_3) \) e \( (x_4, y_4) \), l'area può essere calcolata utilizzando il determinante delle coordinate:
$$ A = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1 - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1) \right| $$
Esempio
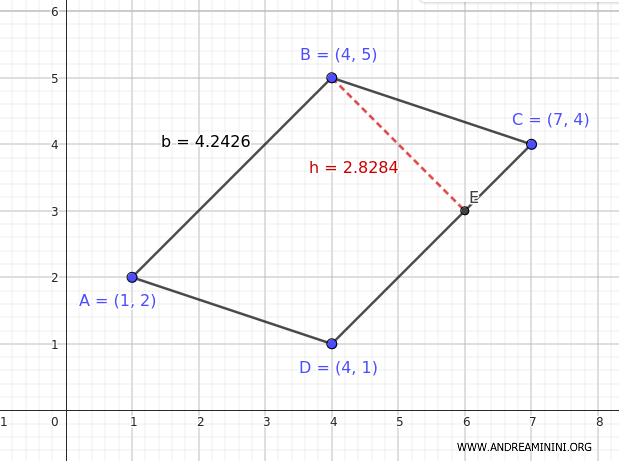
Vediamo un esempio di calcolo dell'area di un parallelogrammo utilizzando le coordinate cartesiane dei suoi vertici.
Supponiamo di avere un parallelogrammo i cui vertici sono dati dalle seguenti coordinate:
$$ A (1, 2) $$
$$ B (4, 5) $$
$$ C (7, 4) $$
$$ D (4, 1) $$
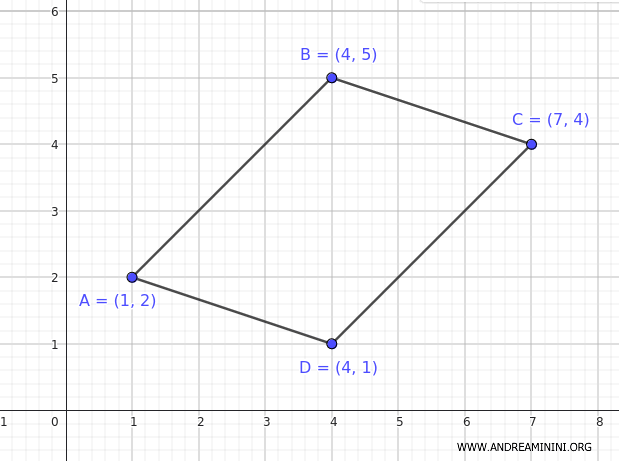
Scrivo le coordinate in ordine ciclico:
$$ (x_1, y_1) = (1, 2) \\
(x_2, y_2) = (4, 5) \\
(x_3, y_3) = (7, 4) \\
(x_4, y_4) = (4, 1) $$
Applico la formula del determinante:
$$ A = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1 - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1) \right| $$
Inserisco le coordinate nella formula:
$$ A = \frac{1}{2} \left| 1 \cdot 5 + 4 \cdot 4 + 7 \cdot 1 + 4 \cdot 2 - (2 \cdot 4 + 5 \cdot 7 + 4 \cdot 4 + 1 \cdot 1) \right| $$
Calcolo i singoli prodotti:
$$ A = \frac{1}{2} \left| 5 + 16 + 7 + 8 - (8 + 35 + 16 + 1) \right| $$
$$ A = \frac{1}{2} \left| 36 - 60 \right| $$
$$ A = \frac{1}{2} \left| -24 \right| $$
$$ A = \frac{1}{2} \cdot 24 $$
$$ A = 12 $$
L'area del parallelogrammo con i vertici dati dalle coordinate \( (1, 2) \), \( (4, 5) \), \( (7, 4) \), \( (4, 1) \) è \( 7.5 \, \text{unità}^2 \).
In effetti, calcolando l'area del parallelogrammo tramite la formula $ A = b \cdot h $ il risultato è A=12.
$$ A = b \cdot h = 4.2426 \cdot 2.8284 = 12 $$
E così via.
