Il teorema del parallelogramma

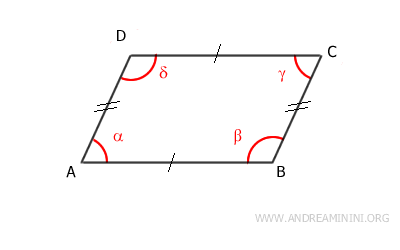
E' sufficiente che una delle condizioni sia soddisfatta per stabilire se un quadrilatero è un parallelogramma oppure no.

Se una delle condizioni è soddisfatta, lo sono anche le altre.

Nota. E' molto importante sottolineare "convesso" perché un parallelogramma è un quadrilatero convesso. Per definizione, un parallelogramma è un quadrilatero convesso con i lati opposti congruenti e paralleli.

La dimostrazione

La dimostrazione è suddivisa in ognuno dei quattro punti.

1] Il quadrilatero è un parallelogramma se i lati opposti sono congruenti

In questo caso l'ipotesi iniziale sono i lati opposti congruenti AB≅CD e AD≅BC.

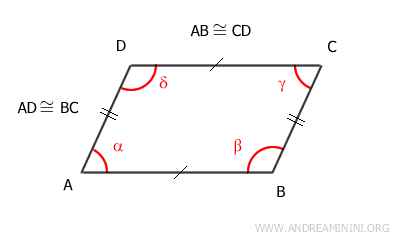
Per dimostrare che il quadrilatero sia un parallelogramma (tesi) devo dimostrare che i lati opposti siano anche paralleli oltre ad essere congruenti.

Traccio una diagonale tra due vertici del parallelogramma. Ad esempio la diagonale AC.

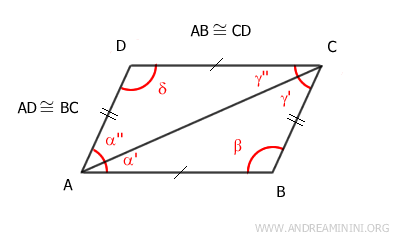
La diagonale suddivide il parallelogramma in due triangoli: ABC e ACD.

I due triangoli ABC e ACD sono congruenti per il terzo criterio di congruenza dei triangoli perché hanno

• Un lato in comune (AC)
• Due lati congruenti per l'ipotesi iniziale AB≅CD e AD≅BC

Sapendo che i due triangoli sono congruenti

$$ ABC \cong ACD $$

Deduco che hanno anche gli angoli congruenti nello stesso ordine

$$ \alpha ' = \gamma '' $$

$$ \alpha '' = \gamma ' $$

$$ \delta = \beta $$

Gli angoli α'≅γ'' sono congruenti e sono anche gli angoli alterni interni delle rette AB e CD tagliate dalla retta AC.

Per l'inverso del teorema delle rette parallele gli angoli alterni interni sono congruenti solo se la trasversale taglia due rette parallele.

Quindi, le rette AB e CD sono rette parallele AB||CD.

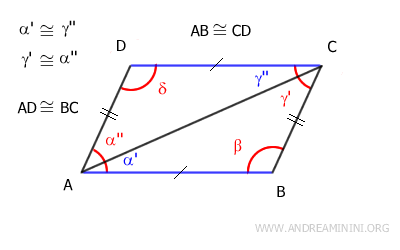
Gli angoli γ'≅α'' sono congruenti e sono anche gli angoli alterni interni delle rette AD e BC tagliate dalla retta AC.

Per l'inverso del teorema delle rette parallele gli angoli alterni interni sono congruenti solo se la trasversale taglia due rette parallele.

Quindi, le rette AD e BC sono rette parallele AD||BC.

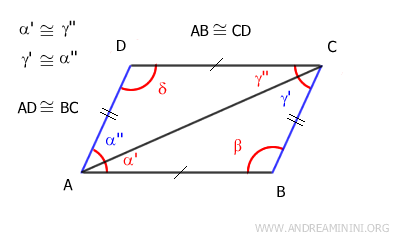
Ho dimostrato che i segmenti AB||CD e AD||BC sono parallleli.

Sapendo per l'ipotesi iniziale che i segmenti AB≅CD e AD≅BC sono anche congruenti, posso dedurre che il quadrilatero è un parallelogramma.

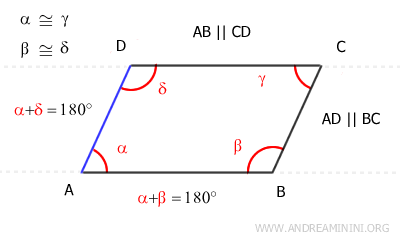
2] Il quadrilatero è un parallelogramma se gli angoli opposti sono congruenti.

In questo caso l'ipotesi iniziale sono gli angoli opposti congruenti α≅γ e β≅δ.

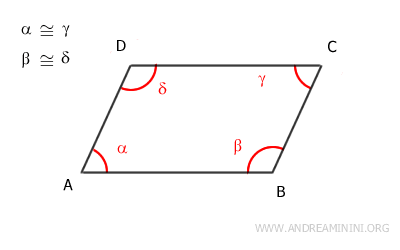
Per affermare che si tratti di un parallelogramma devo dimostrare che i lati opposti sono paralleli e congruenti.

E' un poligono convesso con quattro lati (n=4). Quindi, la somma dei suoi angoli interni è pari a (n-2)·180°=360°

$$ \alpha + \beta + \gamma + \delta = 360° $$

Per l'ipotesi iniziale gli angoli α≅γ e β≅δ sono congruenti.

Sapendo che le somme di angoli congruenti sono congruenti posso scrivere:

$$ \alpha + \beta \cong \gamma + \delta $$

$$ \alpha + \delta \cong \gamma + \beta $$

Sapendo che α+β+γ+δ=360° deduco che la somma α+β=180° e α+δ=180°

$$ \alpha + \beta = 180° $$

$$ \alpha + \delta = 180° $$

Quindi, gli angoli α e β e gli angoli α e δ sono angoli supplementari perché α+β=180° e α+δ=180°.

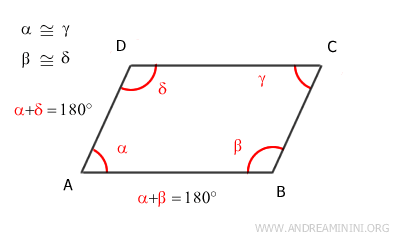
Gli angoli α e β sono angoli supplementari ( α+δ=180° ) e sono anche angoli coniugati interni delle rette AD e BC tagliate dalla trasversale AB.

Quindi, per il teorema inverso delle rette parallele i lati AD e BC del quadrilatero sono paralleli ossia AD||BC

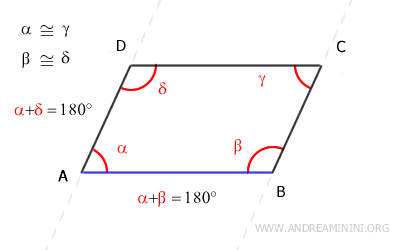
Anche gli angoli α e δ sono angoli supplementari ( α+δ=180° ) e sono anche angoli coniugati interni delle rette AB e CD tagliate dalla trasversale AD.

Quindi, sempre per il teorema inverso delle rette parallele i lati AB e CD del quadrilateri sono paralleli ossia AB||CD

Una volta dimostrato che i lati opposti del quadrilatero sono paralleli AB||CD e AD||BC , resta da dimostrare che i lati opposti siano anche congruenti.

Per dimostrarlo traccio la diagonale AC che suddivide il quadrilatero in due triangoli ABC e ACD.

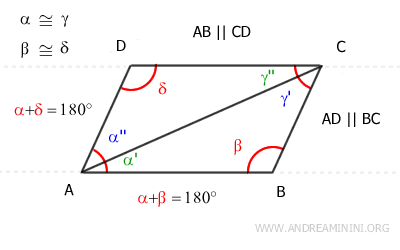
A questo punto applico il teorema delle rette parallele

• Sapendo che le rette AD e BC sono parallele, gli angoli alterni interni α''≅γ' ottenuti con la trasversale AC sono congruenti
• Sapendo che le rette AB e CD sono parallele, gli angoli alterni interni α'≅γ'' ottenuti con la trasversale AC sono congruenti

Questo mi permette di affermare che i triangoli ABC e ACD sono congruenti per il secondo criterio di congruenza dei triangoli in quanto:

• I due triangoli hanno un lato in comune (AC)
• I due triangoli hanno due angoli congruenti α'≅γ'' e γ'≅α''

Una volta stabilito che i triangoli ABC≅ACD sono congruenti, deduco che hanno i lati congruenti nello stesso ordine

In particolar modo, mi interessa sapere che sono congruenti i lati AD≅BC AB≅CD.

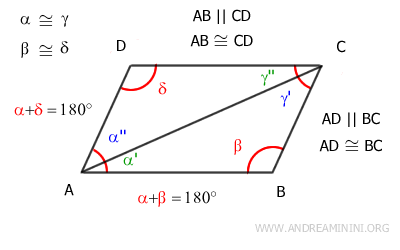
In conclusione, ho dimostrato che i lati opposti del quadrilatero sono paralleli e congruenti.

Quindi, il quadrilatero è un parallelogramma.

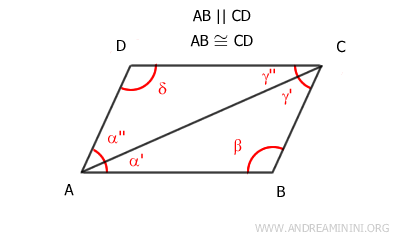
3] Il quadrilatero ha due lati opposti paralleli e congruenti

In questo caso l'ipotesi iniziale sono due lati opposti paralleli e congruenti.

Ad esempio, AB≅CD e AB || CD.

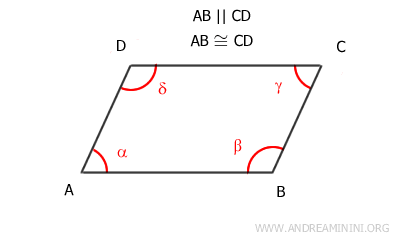
Devo dimostrare che anche gli altri due lati opposti AD e BC sono paralleli e congruenti.

Traccio una diagonale AC che suddivide il quadrilatero in due triangoli ABC e ACD

Sapendo che i segmenti AB e CD sono paralleli per l'ipotesi iniziale (AB || CD), per il teorema delle rette parallele gli angoli alterni interni α'≅γ'' sono congruenti

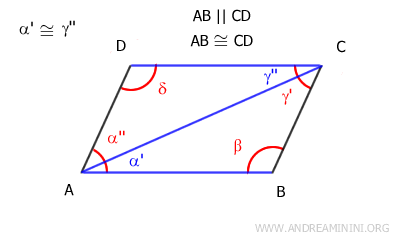
Questo mi permette di affermare che i due triangoli ABC e ACD sono congruenti in base al primo principio di congruenza perché

• Hanno un lato congruente AB≅CD per l'ipotesi iniziale
• Hanno il lato AC in comune per costruzione (la diagonale)
• Hanno l'angolo α'≅γ'' compreso tra i lati congruente

Una volta stabilito che i triangoli ABC≅ACD sono congruenti deduco che hanno tutti i lati e gli angoli congruenti nello stesso ordine.

In particolar modo, mi interessa sapere che i lati AD≅BC sono congruenti e che anche gli angoli α''≅γ' sono congruenti.

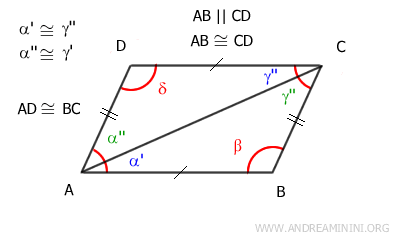
A questo punto ho dimostrato che tutti i lati opposti sono congruenti: AB≅CD e AD≅BC.

Resta da dimostrare che i lati AD e BC siano anche paralleli.

Per farlo basta osservare che gli angoli α''≅γ' sono congruenti e sono anche gli angoli alterni interni delle rette AD e BC tagliate dalla retta AC.

Quindi, per il teorema inverso delle rette parallele i lati AD e BC sono paralleli AD || BC

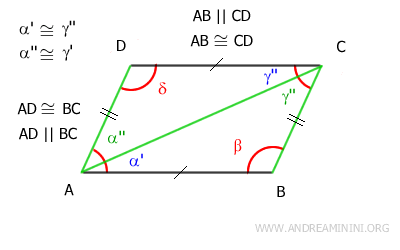
In conclusione, i lati opposti del quadrilatero sono paralleli e congruenti.

Pertanto, il quadrilatero è un parallelogramma.

4] Il quadrilatero è un parallelogramma se le diagonali si intersecano nel loro punto medio

L'ipotesi iniziale è che le diagonali del quadrilatero convesso si incontrano nel loro punto medio.

Pertanto i segmenti AM≅CM e BM≅DM sono congruenti.

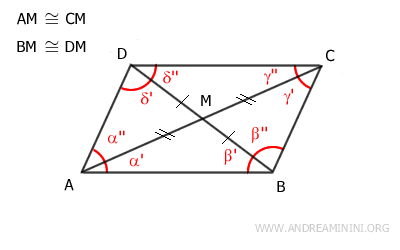
Per affermare che il quadrilatero sia un parallelogramma devo dimostrare che i lati opposti siano paralleli e congruenti.

Gli angoli θ' e θ'' sono angoli opposti al vertice, quindi sono congruenti θ'≅θ''

Questo mi permette di affermare che i triangoli AMD e BMD sono congruenti per il primo criterio di convergenza dei triangoli, perché hanno due lati congruenti e l'angolo tra di essi congruente..

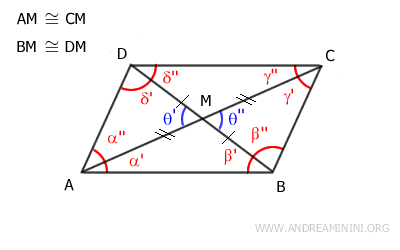
Una volta assodato che i triangoli AMD≅BMC sono congruenti deduco che i lati AD≅BC sono congruenti.

Inoltre, tutti gli angoli dei due triangoli sono congruenti nello stesso ordine.

In particolar modo mi interessa sapere che sono congruenti gli angoli δ'≅β' perché sono anche gli angoli alterni interni delle rette AD e BC tagliate dalla trasversale BD.

Quindi, per il teorema inverso delle rette parallele i lati AD e BC sono anche paralleli AD || BC

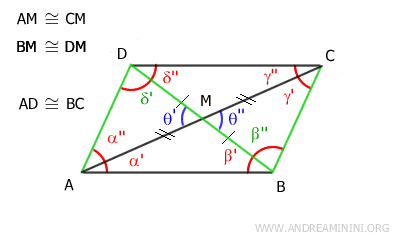
Ripeto lo stesso ragionamento con i triangoli ABM e CDM.

Gli angoli φ' e φ'' sono opposti al vertice, quindi sono congruenti φ'≡φ''

Pertanto, i triangoli ABM e CDM sono congruenti per il primo criterio di convergenza dei triangoli perché hanno due lati congruenti e l'angolo tra di essi congruente.

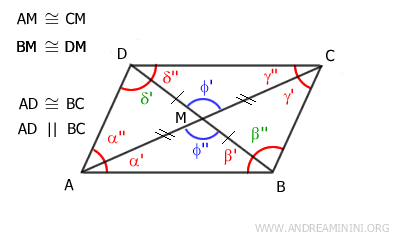
Una volta saputo che i triangoli ABM≅CDM sono congruenti deduco che i lati AB≅CD sono congruenti.

Inoltre, gli angoli dei due triangoli sono congruenti nello stesso ordine.

In particolar modo mi è utile sapere che sono congruenti gli angoli α'≅γ'' perché sono anche gli angoli alterni interni delle rette AB e CD tagliate dalla trasversale AC.

Quindi, per il teorema inverso delle rette parallele i lati AB e CD sono anche paralleli AB || CD

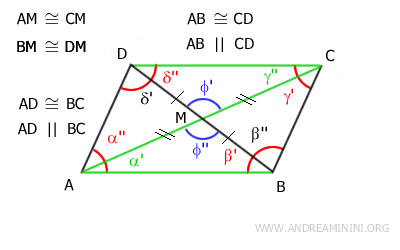
In conclusione i lati opposti del quadrilatero sono congruenti e paralleli.

Pertanto, posso affermare che il quadrilatero è un parallelogramma.

E così via.