Le facce opposte di un parallelepipedo sono congruenti e parallele
Sì può dimostrare che le facce opposte di un parallelepipedo sono congruenti e parallele utilizzando la geometria euclidea.
Dimostrazione
Un parallelepipedo è un solido con sei facce che sono tutte parallelogrammi.
Posso considerare un parallelepipedo con vertici denominati, per esempio, \( A, B, C, D, A', B', C', D' \), dove \( ABCD \) è una faccia, \( A'B'C'D' \) è la faccia opposta e le altre quattro facce sono parallelogrammi.
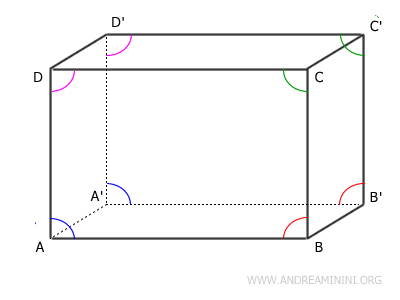
Sapendo che nel parallelepipedo, gli spigoli opposti sono uguali per costruzione:
\( AB = A'B' \)
\( BC = B'C' \)
\( CD = C'D' \)
\( DA = D'A' \)
Inoltre, gli angoli corrispondenti tra due facce opposte sono uguali perché i parallelepipedi sono costruiti con angoli congruenti nei parallelogrammi.
Poiché le due facce hanno gli stessi lati e gli stessi angoli, sono congruenti per il criterio di congruenza dei parallelogrammi.
$$ ABCD \cong A'B'C'D' $$
E lo stesso può dirsi per tutte le altre facce opposte del parallelepipedo.
Dimostrazione della parallelità
Due piani sono paralleli se non si intersecano e se esiste una traslazione che porta uno sull'altro.
Nel caso di un parallelepipedo:
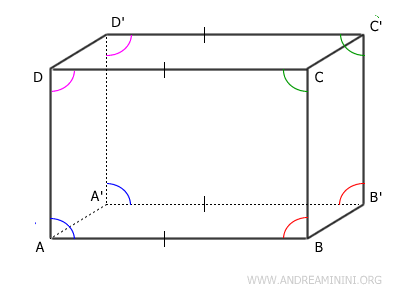
- Ogni coppia di facce opposte è separata da uno spessore costante (la distanza tra i due piani è uguale e costante).
- Gli spigoli delle facce opposte sono paralleli tra loro.
Quindi, le facce opposte si trovano su piani paralleli, il che conferma la loro parallelità.
Ad esempio, sapendo che le facce opposte $ ABCD \cong A'B'C'D' $ sono congruenti, allora le facce $ AA'D'D || BB'C'C $ sono parallele tra loro perché i rispettivi piani si trovano alla stessa distanza $ AB \cong A'B' \cong CD \cong C'D' $. Lo stesso può dirsi per tutte le facce opposte del parallelepipedo.
Conclusione
Ho dimostrato che le facce opposte di un parallelepipedo sono congruenti perché hanno lati e angoli uguali e sono parallele perché si trovano su piani distinti che non si intersecano e sono traslati l'uno rispetto all'altro.
Questa proprietà vale per tutti i parallelepipedi, inclusi i cubi e i prismi rettangolari.
E così via.
