Volume del parallelepipedo
Il volume V di un parallelepipedo è il prodotto dell'area di una delle sue basi AB per l'altezza h. $$ V = A_B \cdot h $$ o, in modo equivalente sapendo che $ A_b = l \cdot w $, il prodotto tra la lunghezza (l), la profondità (w) e l'altezza (h). $$ V = l \cdot w \cdot h $$
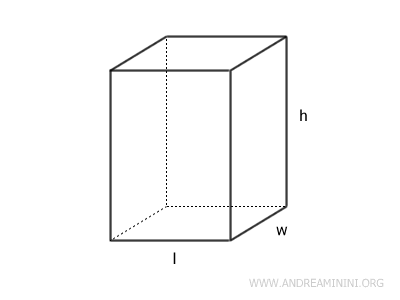
Dimostrazione
Considero quattro parallelepipedi e una unità di misura $ u=1 $
L'ultimo solido è un cubo unitario di volume $ V_4 = u^3 $.
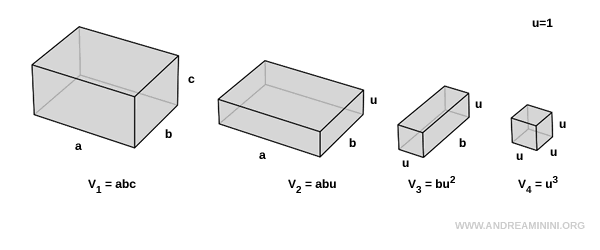
Devo dimostrare che l'area del primo parallelepipedo è effettivamente $ V_1 = abc $.
Provo a dimostrare la formula in modo costruttivo, partendo da un cubo unitario, sapendo che il volume di un solido può essere misurato contando quanti cubi unitari ($ u = 1 $) possono essere collocati al suo interno.
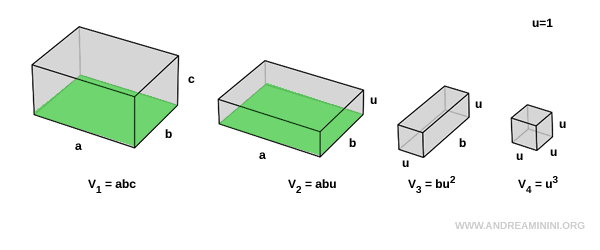
Il primo e il secondo parallelepipedo hanno la stessa area di base $ a \cdot b $ ma diversa altezza ( $ c $ ).
$$ V_1 = a \cdot b \cdot c $$
$$ V_2 = a \cdot b \cdot u $$
Per una proprietà dei prismi, se l'area di base è la stessa il volume è proporzionale alle relative altezze.
$$ V_1 : V_2 = c : u $$
Quindi, il volume del primo parallelepipedo posso scriverla:
$$ V_1 = \frac{c}{u} \cdot V_2 $$
Sapendo che $ u=1 $ diventa:
$$ V_1 = c \cdot V_2 $$
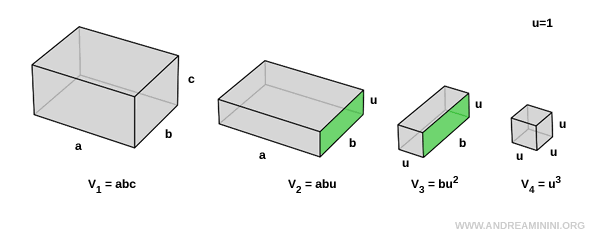
Il secondo e il terzo parallelepipedo hanno la stessa area in una faccia $ b \cdot u $ ma diversa larghezza ( $ a$ ).
$$ V_2 = a \cdot b \cdot u $$
$$ V_3 = u \cdot b \cdot u $$
Anche in questo caso il loro volume è proporzionale.
$$ V_2 : V_3 = a : u $$
Quindi, il volume del secondo parallelepipedo è:
$$ V_2 = \frac{a}{u} \cdot V_3 = a \cdot V_3 $$
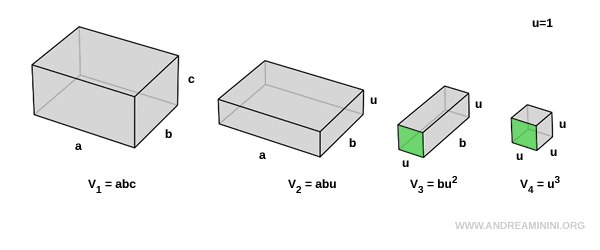
Il terzo e il quarto parallelepipedo hanno la stessa area in una faccia $ u \cdot u $ ma diversa profondità ( $ b $ ).
$$ V_3 = u \cdot b \cdot u $$
$$ V_4 = u \cdot u \cdot u $$
Anche in questo caso il loro volume è proporzionale.
$$ V_3 : V_4 = b : u $$
Quindi, il volume del terzo parallelepipedo è:
$$ V_3 = \frac{b}{u} \cdot V_4 = b \cdot V_4 $$
Ora torno al primo parallelepipedo, il cui volume è
$$ V_1 = c \cdot V_2 $$
Sapendo che $ V_2 = a \cdot V_3 $
$$ V_1 = c \cdot ( a \cdot V_3 ) $$
Sapendo che $ V_3 = b \cdot V_4 $
$$ V_1 = c \cdot ( a \cdot ( b \cdot V_4 ) ) $$
Questo significa che nel volume del primo parallelepipedo ci sono $ a \cdot b \cdot c $ cubi unitari $ V_4 $
$$ V_1 = a \cdot b \cdot c \cdot V_4 $$
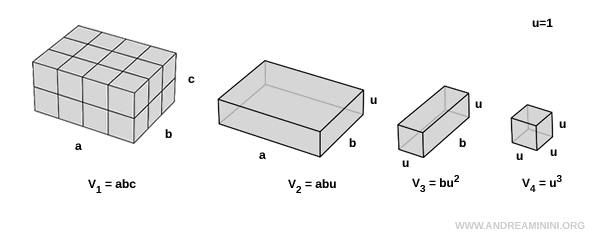
Poiché $ V_4 = u^3 = 1 $
$$ V_1 = a \cdot b \cdot c $$
Questo dimostra che il volume del primo parallelepipedo è il prodotto tra la larghezza, la profondità e l'altezza.
E così via.
