Relazione tra il lato dell'esagono e il raggio del cerchio inscritto
Il lato (l) di un esagono regolare è legato al raggio (r) del cerchio inscritto tramite la seguente formula $$ l = \frac{2 \sqrt{3}}{3} \cdot r $$ 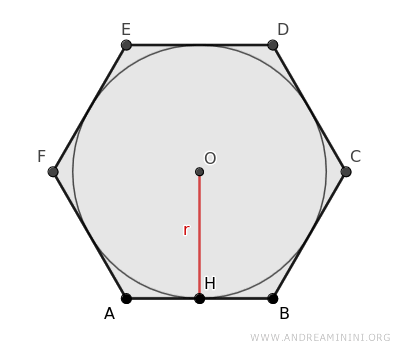
Il raggio del cerchio inscritto coincide con l'apotema dell'esagono r=a, quindi esiste la stessa relazione tra il lato e l'apotema (a) dell'esagono.
$$ l = \frac{2 \sqrt{3}}{3} \cdot a $$
Quest'ultima formula è molto più conosciuta ma è sostanzialmente uguale alla precedente.
Le formule inverse. Allo stesso modo posso calcolare la lunghezza del raggio inscritto (r) a partire dal lato (l) dell'esagono usando la formula inversa $$ r = l \cdot \frac{3}{2 \sqrt{3}} = l \cdot \frac{\sqrt{3} }{2} $$ o l'apotema dell'esagono $$ a = l \cdot \frac{3}{2 \sqrt{3}} = l \cdot \frac{\sqrt{3} }{2} $$
Un esempio pratico
Considero un esagono regolare con i lati di lunghezza 2 e il raggio del cerchio inscritto r=1.7321
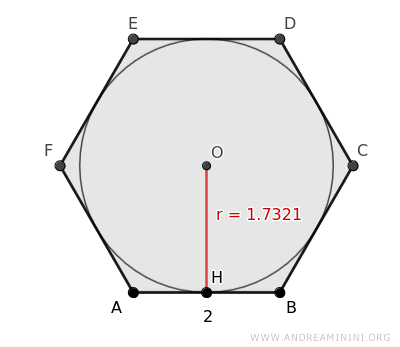
Applico la formula per calcolare la lunghezza del lato a partire dal raggio del cerchio inscritto.
$$ l = \frac{2 \sqrt{3}}{3} \cdot r $$
In questo caso il raggio è r=1.7321
$$ l = \frac{2 \sqrt{3}}{3} \cdot 1.7321 $$
Svolgo i calcoli e ottengo esattamente la lunghezza del lato dell'esagono.
$$ l = 2 $$
Dove il raggio (r) è anche l'apotema (a) dell'esagono.
La dimostrazione
Prendo in considerazione un esagono e un cerchio inscritto con centro O e raggio r.

Il centro del cerchio inscritto è anche il centro dell'esagono regolare perché è il punto in cui si incontrano le diagonali.
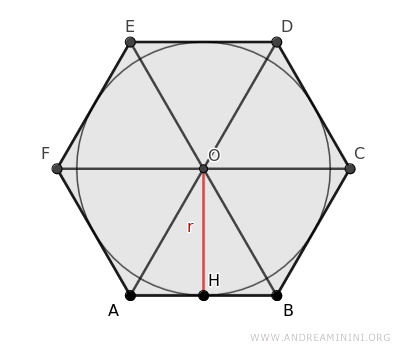
Le diagonali suddividono la superficie dell'esagono in sei triangoli, dividendo l'angolo al centro in sei parti congruenti di ampiezza 360°/6=60°.
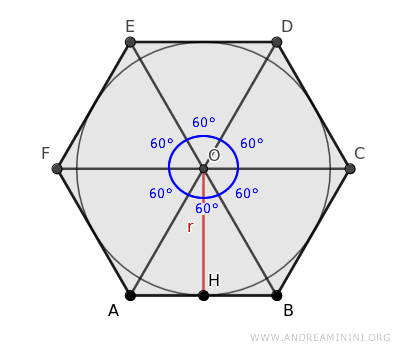
Questi triangoli sono congruenti perché, secondo il criterio di congruenza dei triangoli, hanno due lati congruenti e l'angolo tra di essi congruente (60°) .
Questo mi permette di concentrare l'analisi su un solo triangolo tra questi, ad esempio sul triangolo ABO.
Le diagonali dividono gli angoli interni dell'esagono (120°) in due angoli congruenti di 60°.
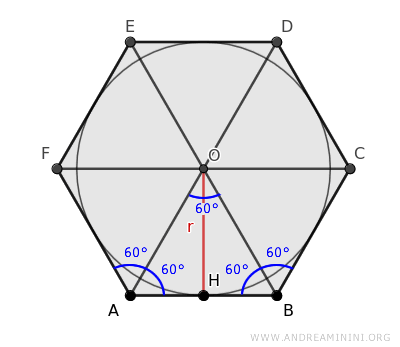
Questo significa che il triangolo ABO ha tutti gli angoli congruenti a 60° ed è un triangolo equilatero.
A questo punto devo trovare il legame tra il raggio (r) del cerchio inscritto e il lato (l) dell'esagono.
Il raggio r suddivide il triangolo equilatero ABO in due triangoli rettangoli AHO e BHO.
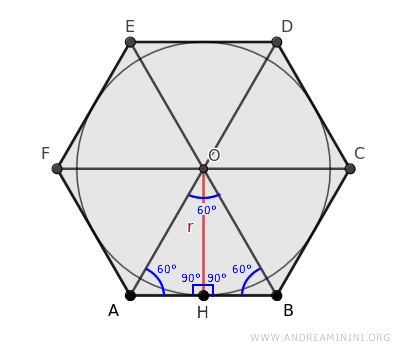
Quindi, posso utilizzare il teorema di Pitagora su uno dei due triangoli rettangoli per calcolare la lunghezza del cateto OH (raggio r).
Ad esempio, applico Pitagora sul triangolo AHO.
$$ \overline{OH} = \sqrt{\overline{AO}^2 - \overline{AH}^2} $$
Il segmento OH coincide con il raggio r del cerchio inscritto
$$ r = \sqrt{\overline{AO}^2 - \overline{AH}^2} $$
Il segmento AO è congruente con il lato dell'esagono (l) poiché il triangolo ABO è equilatero.
$$ r = \sqrt{l^2 - \overline{AH}^2} $$
Il segmento AH è la metà del lato dell'esagono (l/2).
$$ r = \sqrt{l^2 - ( \frac{l}{2} )^2} $$
Svolgo i calcoli algebrici.
$$ r = \sqrt{l^2 - \frac{l^2}{4} } $$
$$ r = \sqrt{ \frac{4l^2-l^2}{4} } $$
$$ r = \sqrt{ \frac{3l^2}{4} } $$
$$ r = \frac{l}{2} \sqrt{ 3 } $$
A questo punto ricavo il lato.
$$ r \cdot \frac{ 2 }{ \sqrt{3} } = \frac{l}{2} \sqrt{ 3 } \cdot \frac{ 2 }{ \sqrt{3} } $$
$$ r \cdot \frac{ 2 }{ \sqrt{3} } = l $$
Per portare il radicale al numeratore, moltiplico e divido la frazione nel membro di sinistra dell'equazione per la radice quadrata di tre.
$$ r \cdot \frac{ 2 }{ \sqrt{3} } \cdot \frac{ \sqrt{3} }{ \sqrt{3} } = l $$
$$ r \cdot \frac{ 2 \sqrt{3} }{ \sqrt{3} \cdot \sqrt{3} } = l $$
$$ r \cdot \frac{ 2 \sqrt{3} }{ \sqrt{3 \cdot 3} } = l $$
$$ r \cdot \frac{ 2 \sqrt{3} }{ \sqrt{3^2} } = l $$
$$ r \cdot \frac{ 2 \sqrt{3} }{ 3 } = l $$
Infine, riordino i termini
$$ l = \frac{ 2 \sqrt{3} }{ 3 } \cdot r $$
Questo dimostra l'esistenza della formula che lega il raggio (r) del cerchio inscritto al lato (l) dell'esagono regolare.
Nota. Sapendo che il raggio del cerchio inscritto coincide con l'apotema dell'esagono regolare r=a, posso scrivere la formula anche in questa forma equivalente $$ l = \frac{ 2 \sqrt{3} }{ 3 } \cdot a $$
E così via.
