Il lato di un esagono è uguale al raggio del cerchio circoscritto
La lunghezza del lato di un esagono regolare corrisponde esattamente a quella del raggio della circonferenza circoscritta all'esagono.
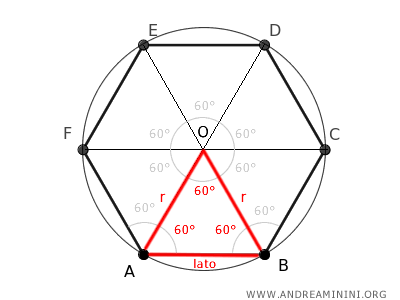
Questo si verifica perché un esagono regolare può essere diviso in sei triangoli equilateri congruenti.
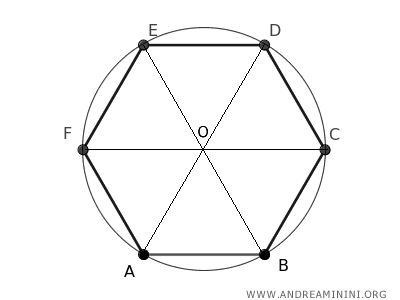
Ogni triangolo ha per base un lato dell'esagono e per lati obliqui i raggi che vanno dal centro dell'esagono, che è anche il centro del cerchio circoscritto, ai vertici dell'esagono.
Questi triangoli sono equilateri perché hanno tutti i lati e gli angoli congruenti.
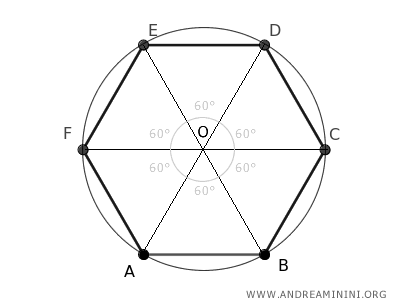
L'angolo giro al centro O di 360° viene suddiviso in sei parti congruenti, ovvero in sei angoli di 60°.
Quindi, l'angolo opposto alla base di ogni triangolo ha un'ampiezza pari a 60°.
Sapendo che tutti gli angoli interni di un esagono regolare hanno un'ampiezza di 120°, deduco che anche gli angoli adiacenti alla base dei triangoli sono pari a 60°.
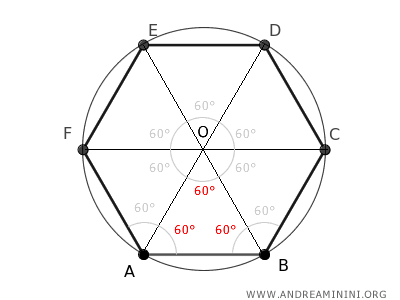
Questo dimostra che tutti i triangoli in cui ho suddiviso l'esagono sono triangoli equilateri, perché hanno tutti gli angoli congruenti a 60°.
La base di ogni triangolo è anche un lato dell'esagono, e i due lati obliqui sono i raggi del cerchio.
Dato che tutti i lati di un triangolo equilatero sono uguali, segue che la lunghezza del raggio (che è il lato obliquo del triangolo) è uguale alla lunghezza del lato dell'esagono.

Questa proprietà degli esagoni regolari li rende particolarmente utili in varie dimostrazioni geometriche e nella vita reale.
E così via.
