Il lato di un esagono regolare è uguale al raggio della circonferenza circoscritta
Il lato di un esagono regolare è congruente al raggio della circonferenza circoscritta all'esagono.
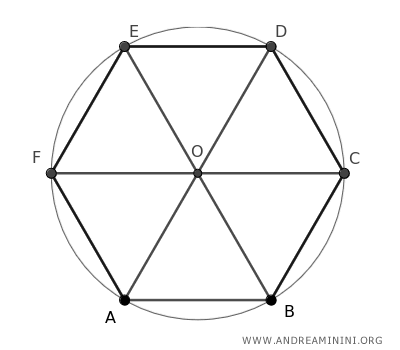
Ad esempio $$ \overline{AB} \cong \overline{OA} $$
Questa proprietà degli esagoni regolari è dovuta al fatto che un esagono può essere scomposto in 6 triangoli equilateri.
La dimostrazione
Traccio dei segmenti tra il centro O e i vertici A, B, C, D, E, F dell'esagono regolare.

In questo modo suddivido l'esagono in sei triangoli isosceli ABO, BCO, CDO, DEO, EFO, FAO.
Sono tutti triangoli isosceli in quanto i lati obliqui coincidono con la circonferenza circoscritta.
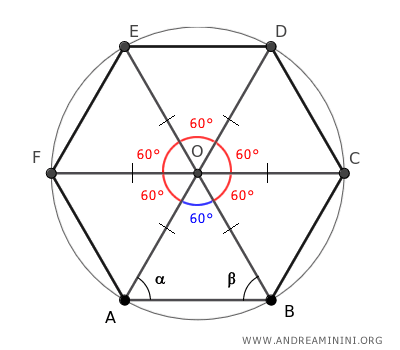
L'angolo giro al centro viene diviso in sei parti congruenti.
Quindi, l'angolo al vertice O di ogni triangolo ha un'ampiezza di 60°.
$$ 360° \cdot \frac{1}{6} = 60° $$
Pertanto, secondo il primo principio di congruenza tutti i triangoli sono congruenti perché hanno due lati congruenti e l'angolo tra questi congruente.
$$ ABO \cong BCO \cong CDO \cong DEO \cong EFO \cong FAO $$
Resta da dimostrare che sono anche equilateri.
Essendo triangoli congruenti, proseguo lo studio su un triangolo tra questi. Ad esempio, considero il triangolo ABO.

Sapendo che la somma degli angoli di un triangolo è sempre uguale a 180° sul piano, deduco che la somma degli angoli restanti del triangolo ABO è uguale a 120°
$$ \alpha + \beta + 60° = 180° $$
$$ \alpha + \beta = 180° - 60° $$
$$ \alpha + \beta = 120° $$
Il triangolo ABO è un triangolo isoscele, quindi ha gli angoli adiacenti alla base congruenti.
$$ \alpha \cong \beta $$
Pertanto gli angoli α e β sono congruenti alla metà di 120° ovvero hanno un'ampiezza di 60°
$$ \alpha \cong \beta \cong \frac{120°}{2} = 60° $$
Ora conosco l'ampiezza di tutti gli angoli del triangolo ABO
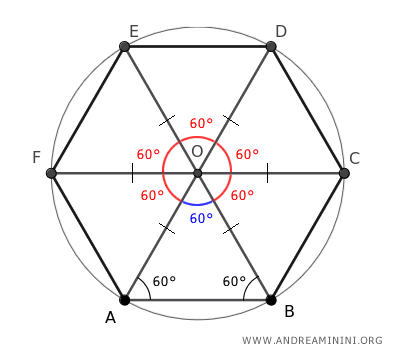
Il triangolo ABO ha tutti gli angoli uguali a 60°, quindi anche i suoi lati sono congruenti.
$$ \overline{AO} \cong \overline{BO} \cong \overline{AB} $$
Questo vuol dire che il triangolo ABO è un triangolo equilatero.
Pertanto, il lato AB del triangolo ABO è congruente al lato obliquo AO della circonferenza.
$$ \overline{AO} \cong \overline{AB} $$
Lo stesso vale per tutti gli altri lati dei triangoli in cui ho suddiviso l'esagono, perché ho già dimostrato che i triangoli sono tra loro congruenti.
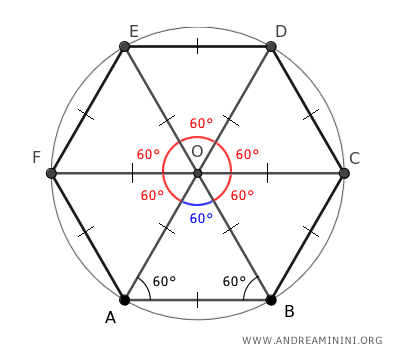
In conclusione, i lati dell'esagono sono congruenti al raggio della circonferenza in cui l'esagono è inscritto.
E così via.
