I poliedri
Un poliedro è una figura solida tridimensionale delimitata da facce piatte, spigoli e vertici.
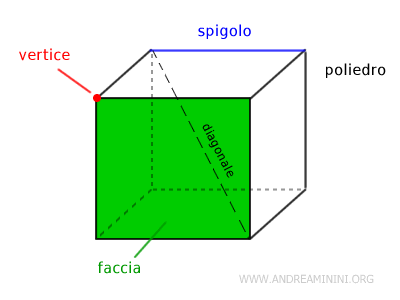
Le facce di un poliedro sono poligoni (es. triangoli, quadrati, pentagoni, ecc.) appartenenti a piani diversi, tali che ogni piano non attraversi il solido. Un poliedro ha almeno quattro facce (tetraedro). Il pentaedro ha cinque facce, l'esaedro ne ha sei, l'ottaedro ne ha otto, ecc.
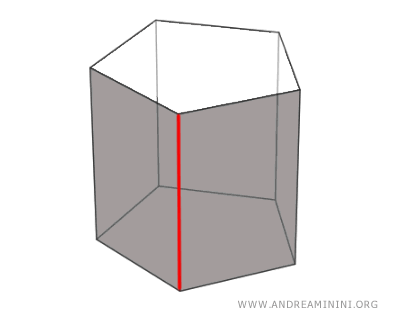
Gli spigoli sono i punti di intersezione tra le facce del poliedro. Sono i lati dei poligoni in ogni faccia del poliedro.
A ogni spigolo del poliedro è associato un diedro composto dalle due facce che contengono quello spigolo
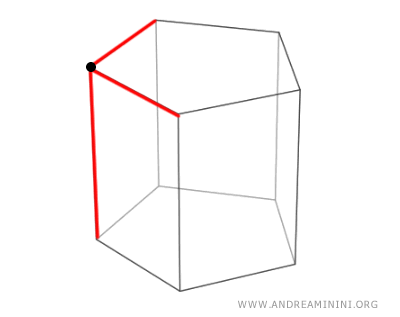
I vertici sono i punti in cui si incontrano tre o più spigoli. Sono i vertici dei poligoni.
A ogni vertice del poliedro è associato un angoloide composto dagli spigoli che escono dal vertice.
Fin dall'antichità i poliedri hanno catturato l'interesse di matematici, artisti e filosofi per millenni. Ad esempio, Platone era particolarmente interessato ai poliedri regolari, da cui prendono il nome di "solidi platonici". Oltre che in matematica, i poliedri hanno diverse applicazioni in ambito scientifico e ingegneristico. Ad esempio, in chimica molte strutture molecolari assumono la forma di un poliedro. Inoltre, sono ampiamente usati in architettura e anche in ambito artistico.
La diagonale di un poliedro è il segmento che congiunge due vertici che non si trovano sulla stessa faccia.
La superficie totale di un poliedro è la somma delle superfici di tutte le sue facce.
Poliedri regolari e irregolari
I poliedri si distinguono i poliedri regolari o irregolari.
- Poliedri regolari (o solidi platonici)
I poliedri regolari sono solidi con facce poligonali regolari congruenti e anche i loro diedri e angoloidi sono congruenti. Sono anche conosciuti come solidi platonici.Nota. Nel piano i poligoni regolari possono avere un numero qualsiasi di lati. Nello spazio, invece, esistono solo cinque poliedri regolari: tetraedro, esagono, ottaedro, dodecaedro e icosaedro.
- Poliedri irregolari
I poliedri irregolari non hanno facce o angoli identici. Ad esempio, il prisma è un esempio tipico di poliedro irregolare, perché può avere basi di qualsiasi forma poligonale.
La formula di Eulero
La formula di Eulero individua una relazione il numero di vertici (V), di spigoli (E) e di facce (F) di un poliedro semplice e connesso (senza buchi).
In un poliedro semplice e connesso il numero di vertici (V) meno il numero di spigoli (E) più il numero di facce (F) è sempre uguale a 2. $$ V - E + F = 2 $$
Ad esempio, il cubo ha 6 facce quadrate, 8 vertici e 12 spigoli.
$$ F = 6 $$
$$ V = 8 $$
$$ E = 12 $$
Sostituisco questi valori nella formula di Eulero
$$ V - E + F = 2 $$
$$ 6 - 12 + 8 = 2 $$
$$ 2 = 2 $$
L'equazione è soddisfatta.
A cosa serve? Posso usare la formula di Eulero per verificare se una combinazione di vertici, spigoli e facce può formare un poliedro semplice e connesso. Se non soddisfa la formula di Eulero, allora la combinazione non rappresenta un poliedro di questo tipo. Ad esempio, è stata usata per dimostrare che ci sono esattamente cinque poliedri regolari (i solidi platonici).
Solidi platonici
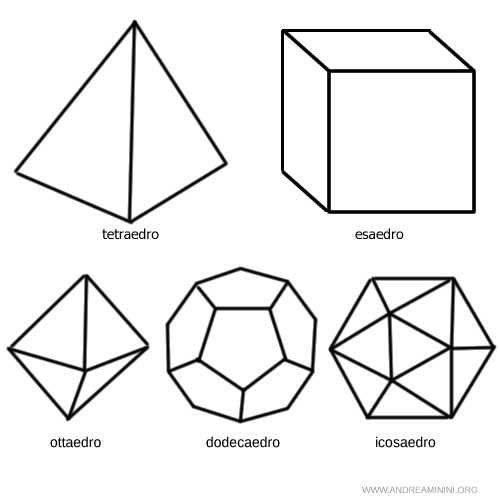
I solidi platonici sono i cinque solidi regolari conosciuti.
- Tetraedro
E' un poliedro con 4 facce triangolari, 4 vertici e 6 spigoli. Ogni faccia è un triangolo equilatero. - Esaedro
Questo poliedro regolare è conosciuto soprattutto come "cubo". Ha 6 facce quadrate, 8 vertici e 12 spigoli. Ogni faccia è un quadrato. - Ottaedro
Ha 8 facce triangolari, 6 vertici e 12 spigoli. - Dodecaedro
E' un poliedro con 12 facce pentagonali, 20 vertici e 30 spigoli. Ogni faccia è un pentagono. - Icosaedro
Ha 20 facce triangolari, 12 vertici e 30 spigoli.
Dimostrazione
Si può dimostrare che i poliedri regolari sono solo cinque, considerando che in un angoloide la somma degli angoli delle facce è sempre minore di un angolo giro (360°).
Ad esempio, considero un poliedro regolare che ha le facce composte da triangoli equilateri congruenti.
In un triangolo equilatero ogni angolo ha un'ampiezza di 60°. Quindi, il poliedro può avere al massimo 5 facce perché la somma degli angoli di un angolide deve essere inferiore a un angolo giro $ 6 \times 60° = 360° $.
| Poligono regolare | Numero di facce in un vertice | Somma degli angoli delle facce | Poliedro |
|---|---|---|---|
| triangoli equilateri (angoli di 60°) |
3 | 180° < 360° | tetraedro |
| 4 | 240° < 360° | ottaedro | |
| 5 | 300° < 360° | icosaedro | |
| 6 | 360° = 360° | non esiste |
Considero ora un poliedro regolare le cui facce sono quadrati.
Poiché ciascun angolo di un quadrato misura 90°, in un vertice del poliedro possono convergere al massimo 3 facce: infatti, la somma degli angoli di un angolide deve essere inferiore all'angolo giro \( 4 \times 90^\circ = 360^\circ \).
| Poligono regolare | Numero di facce in un vertice | Somma degli angoli delle facce | Poliedro |
|---|---|---|---|
| quadrati (angoli di 90°) |
3 | 270° < 360° | esaedro |
| 4 | 360° = 360° | non esiste |
Considero un poliedro regolare le cui facce sono pentagoni.
Poiché ciascun angolo di un pentagono regolare misura 108°, in un vertice del poliedro possono convergere al massimo 3 facce: infatti, se fossero 4 la somma degli angoli di un angolide supererebbe l'angolo giro \( 4 \times 108^\circ = 432° > 360^\circ \).
| Poligono regolare | Numero di facce in un vertice | Somma degli angoli delle facce | Poliedro |
|---|---|---|---|
| pentagoni (angoli di 108°) |
3 | 324° < 360° | dodecaedro |
| 4 | 432° > 360° | non esiste |
Ora prendo in considerazione un poliedro regolare le cui facce sono esagoni.
Poiché ciascun angolo di un esagono regolare misura 120°, un angolide deve avere almeno tre spigoli e la somma dei suoi angoli deve essere strettamente inferiore a 360°, deduco che questo poliedro regolare non può esistere \( 3 \times 120^\circ = 360^\circ \).
| Poligono regolare | Numero di facce in un vertice | Somma degli angoli delle facce | Poliedro |
|---|---|---|---|
| esagoni (angoli di 120°) |
3 | 360° = 360° | non esiste |
A questo punto è inutile analizzare altri poligoni regolari con più lati.
Questo dimostra che esistono solo cinque poliedri regolari (tetraedro, ottaedro, icosaedro, esaedro, dodecaedro).
Il diedro del poliedro
A ogni spigolo del poliedro è associato un diedro, detto diedro del poliedro, generato dalle due facce che contengono lo spigolo.
Ad esempio, ogni spigolo del cubo è l'intersezione tra due quadrati che risiedono su due semipiani.
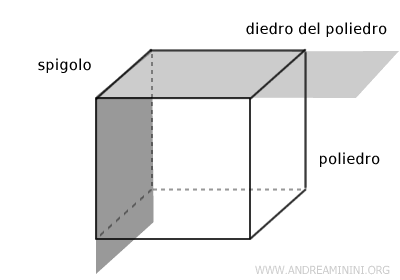
Il diedro associato allo spiegolo è un diedro del poligono.
Lo sviluppo di un poliedro
La superficie totale di un poliedro è uguale alla somma delle superfici delle sue facce.
Spesso, per studiare la superficie totale di un poliedro, si ricorre allo sviluppo della superficie poliedrica su un piano.
Lo sviluppo di un poliedro è la rappresentazione bidimensionale del solido. Si ottiene "srotolando" le varie facce del poliedro, in modo da formare una figura piana.
Lo sviluppo mi permette di visualizzare tutte le facce del poliedro in un unico piano senza sovrapposizioni, mantenendo le proporzioni e le connessioni tra le varie facce.
In questo modo è più semplice e intuitivo studiare la superficie laterale e la superficie di base del poliedro.
Esempio
Lo sviluppo di un cubo è una figura a forma di croce composta da 6 quadrati, ognuno dei quali rappresenta una faccia del cubo.
Ogni lato dei quadrati nel piano corrisponde a uno spigolo del cubo.
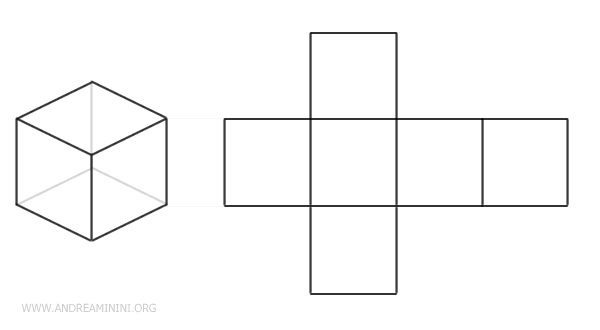
E' solo uno dei tanti modi possibili per sviluppare un cubo.
Nello sviluppo dei parallelepipedi, invece, si utilizzano superfici rettangolari.

Le superfici centrali sono quelle laterali del parallelepipedo mentre le superfici sopra e sotto sono le basi.
E così via.
