Cos'č uno scalare?
In matematica uno scalare è un numero.
Esempio. Sono esempi di scalari i seguenti: 3, 3.3, 10, 25, 73.2, ecc.
In algebra lineare è generalmente indicato con una lettera minuscola in corsivo.
$$ n $$
Spesso lo scalare è affiancato dalla relazione di appartenenza a un insieme di numeri ( reali, interi, ecc. ).
Esempio. Se lo scalare s è un numero reale $$ s \in R $$ Se lo scalare i è un numero intero $$ i \in N $$
Si distingue da altri oggetti come i vettori, le matrici, ecc.
Qual è la differenza tra scalare e vettore
In fisica e matematica le grandezze sono distinte in scalari e vettoriali.
- Scalare
E' una grandezza determinata da un valore numerico detto modulo. - Vettore
E' una grandezza determinata da un valore numerico (modulo), una direzione e un verso.
Pertanto, la grandezza scalare non ha una dimensione nello spazio.
Perché si chiama scalare?
Ci sono diverse spiegazioni sull'origine del nome.
- Il termine "scalare" deriva dal fatto che il valore numerico è spesso associato a una scala di misura.
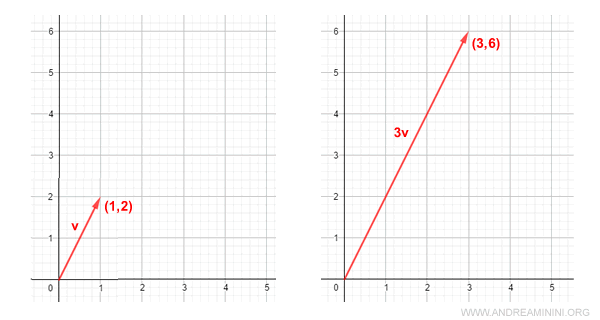
- Un'altra possibile spiegazione è la relazione tra lo scalare e un vettore. Il prodotto tra uno scalare e un vettore modifica soltanto il modulo del vettore, lasciando invariata la direzione e il verso. Pertanto, il vettore cambia dimensioni in base a un fattore di scala.
Esempio. Moltiplico lo scalare a=3 per un vettore V=(1,2). $$ a \cdot V = 3 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 3 \cdot 1 \\ 3 \cdot 2 \end{pmatrix} = \begin{pmatrix} 3 \\ 6 \end{pmatrix} $$ Il vettore cambia dimensione (modulo) ossia la scala ma non il verso, né la direzione.
E così via.
