Riferimento cartesiano
Un riferimento cartesiano (RC) è un riferimento affine sul piano associato a un prodotto scalare <.,.> su R2, in cui i vettori i e j formano una base ortonormale. $$ RC(O,i,j) $$
Un esempio pratico
In un riferimento affine RA(O,i,j) seleziono tre punti (O,i,j).
- Il punto O è l'origine
- Il punto i è il vettore unità delle ascisse
- Il punto j è il vettore unità delle ordinate
Scelgo come vettori i e j i seguenti vettori:
$$ i \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$ $$ j \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$
Dal punto di vista grafico il riferimento affine RA è il seguente:
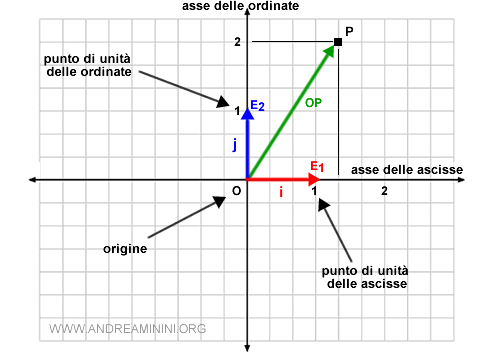
I vettori i e j formano una base dello spazio vettoriale V=R2 perché la loro combinazione lineare può generare qualsiasi altro vettore dello spazio vettoriale.
$$ B = \begin{pmatrix} i , j \end{pmatrix} = \begin{Bmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} \end{Bmatrix} $$
Un riferimento affine (RA) è un riferimento cartesiano (RC) se la base è ortonormale.
Quindi, devo verificare se la base B è una base ortonormale.
Cos'è una base ortonormale? Una base si dice base ortonormale se è composta da vettori ortogonali v,w con prodotto scalare uguale a zero tra vettori diversi e uguale a uno tra vettori uguali $$ <v,w> = 0 \:\: se \:\: v≠w \\ <v,w> = 1 \:\: se \:\: v=w $$
Calcolo il prodotto scalare <.,.> dei vettori della base.
$$ < i,j > = < \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} > = 1 \cdot 0 + 0 \cdot 1 = 0 $$
Il prodotto scalare di due vettori diversi è effettivamente uguale a zero.
Nota. Ci sono diversi prodotti scalari. In questo caso ho usato il prodotto scalare euclideo.
A questo punto devo soltanto verificare che sia uguale a uno il prodotto scalare tra due vettori uguali.
$$ < i,i > = < \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 1 \\ 0 \end{pmatrix} > = 1 \cdot 1 + 0 \cdot 0 = 1 $$
$$ < j,j > = < \begin{pmatrix} 0 \\ 1 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} > = 0 \cdot 0 + 1 \cdot 1 = 1 $$
Il prodotto scalare tra vettori uguali è pari a uno.
Pertanto, la base B è una base ortonormale.
Posso così affermare che RC è un riferimento cartesiano.
