Le disequazioni

Una disequazione è una diseguaglianza tra due espressioni letterali e/o numeriche confrontate tra loro rispetto a una relazione d'ordine ( < , > , ≤ , ≥ ) $$ P(x) > Q(x) $$

Le lettere di cui si cerca il valore sono le incognite della disequazione.

Ecco un esempio pratico di disequazione

$$ x+2 > 4 $$

In questo esempio la lettera x è la variabile incognita, mentre il simbolo ">" indica la relazione d'ordine.

Risolvere una disequazione vuol dire trovare i valori dell'incognita ( dette soluzioni ) che soddisfano la relazione d'ordine della diseguaglianza.

Nota. Una disequazione può essere composta da una o più incognite. Inoltre, può avere una, nessuna o più soluzioni. Se le soluzioni sono più di una si parla di insieme delle soluzioni della disequazione.

Ogni disequazione posso scriverla anche in forma normale spostando i letterali e i numeri a un solo lato della diseguaglianza.

$$ P(x)+Q(x)>0 $$

Esempio. Un esempio di disequazione è la seguente $$ x+2 > 4 $$ che posso riscrivere in forma normale $$ x+2 - 4 > 0 $$ ossia $$ x-2 > 0 $$

I simboli usati in una disequazione per indicare la relazione d'ordine sono i seguenti

<	minore
>	maggiore
≤	minore o uguale
≥	maggiore o uguale

I simboli minore uguale (≤) e maggiore-uguale (≥) indicano una condizione meno restrittiva perché ammettono come soluzione anche l'uguaglianza. In questo caso le radici sono incluse nell'insieme delle soluzioni.

Un esempio pratico

Un esempio di disequazione è la seguente

$$ x-2 > 0 $$

Questa disequazione è soddisfatta quando l'incognita x assume un valore compreso nell'intervallo aperto

$$ x \in (2,+\infty) $$

Qualsiasi valore x>2 soddisfa l'equazione perché il lato sinistro della disequazione x-2 è maggiore di zero.

Pertanto, l'insieme delle soluzioni S della disequazione è

$$ S = \{ \ \forall \ x \in R \ | \ x>2 \ \} $$

Nota. Si legge "per ogni (∀) x appartenente all'insieme dei numeri reali (R) tale che ( | ) la x è maggiore di 2".

La rappresentazione delle soluzioni

Per rappresentare graficamente l'insieme delle soluzioni di una disequazione, in genere si utilizza una retta orientata in cui ogni punto corrisponde a un numero reale da -∞ a +∞.

• Disegno una linea continua per rappresentare l'insieme delle soluzioni della disequazione, ossia l'insieme dei valori dell'incognita che soddisfano la disequazione.
• Non disegno gli altri tratti della retta che non corrispondono alle soluzioni della disequazione.

Esempio. La disequazione x-2>0 è soddisfatta per ogni valore dell'incognita x maggiore di 2 ossia x>2. Per rappresentare l'insieme delle soluzioni traccio una linea continua dal punto 2 della retta in poi, verso destra. Con questa rappresentazione sto dicendo che le soluzioni della disequazione sono tutti i valori reali dell'intervallo (2,∞).

La linea continua va tracciata anche se le soluzioni sono valori negativi. Ad esempio, la disequazione x+2>0 è soddisfatta per qualsiasi valore x>-2. In questo caso l'estremo della freccia comincia dal numero negativo -2.

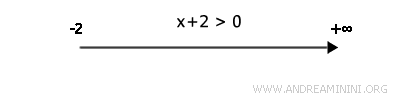
Per quanto riguarda i punti estremi degli intervalli

• utilizzo un cerchietto pieno per indicare che il valore è una soluzione della disequazione
• utilizzo un cerchietto vuoto per indicare che il valore non è una soluzione della disequazione

Esempio. La disequazione x-2>0 è soddisfatta per ogni valore dell'incognita x maggiore di 2 ossia x>2. In questo caso l'estremo x=2 non è una soluzione della disequazione. Quindi, devo indicare il punto x=2 con un cerchietto vuoto.

Viceversa, la disequazione x-4≤0 è soddisfatta per ogni valore dell'incognita x minore o uguale a 4 ossia x≤4. In questo caso, l'estremo x=4 è una soluzione della disequazione. Quindi, devo indicare il punto x=4 con un cerchietto pieno.

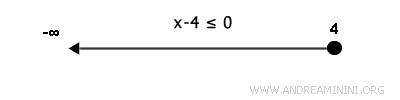
Come risolvere una disequazione con lo studio del segno

In una funzione continua il passaggio da valori positivi a negativi avviene in particolari punti detti punti zero o radici.

Nota. Una radice è un valore dell'incognita x in cui l'espressione della disequazione è uguale a zero. Per trovare le radici basta trasformare la disequazione in un'equazione e risolverla. Ad esempio, la disequazione $$ x - 2 > 0 $$ diventa $$ x - 2 = 0 $$ che si risolve con x=2. Quindi x=2 è una radice della disequazione.

Quindi, il primo passo è cercare le radici della disequazione.

Una volta trovate le radici, se esistono, si può studiare il segno dell'espressione negli intervalli tra le radici.

Nello studio del segno è molto utile disegnare uno schema grafico.

Esempio

Questa disequazione è soddisfatta se l'espressione sul lato sinistro è maggiore di zero.

$$ x \cdot (x-2) > 0 $$

Per risolvera cerco di capire quali sono le radici della disequazione

$$ x \cdot (x-2) = 0 $$

Trattandosi di un prodotto tra x e (x-2) è evidente che l'equazione si annulla quando x=0 oppure x=2.

Quindi, x=0 e x=2 sono le radici della disequazione.

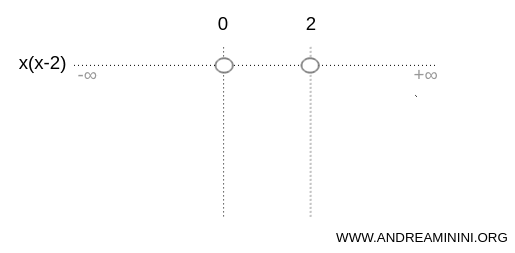
Nota. Nella rappresentazione grafica i cerchietti pieni indicano che il valore considerato è una soluzione (intervallo chiuso). Viceversa, i cerchietti vuoti indicano che il valore non è una soluzione (intervallo aperto). In questo caso sono vuoti perché in x=0 e x=2 la disequazione x(x-2)>0 non è soddisfatta.

Le radici suddividono il campo di definizione della disequazione in tre parti

$$ (- \infty ; 0) \cup (0;2) \cup (2;+\infty) $$

Per studiare il segno della disequazione la scompongo in due espressioni x e (x-2) poiché si tratta di un prodotto.

Poi studio il segno delle espressioni negli intervalli (-∞;0) , (0;2) e (2;∞)

L'espressione x è negativa nell'intervallo (-∞;0), è nulla nel punto x=0 ed è positiva nell'intervallo (0;∞).

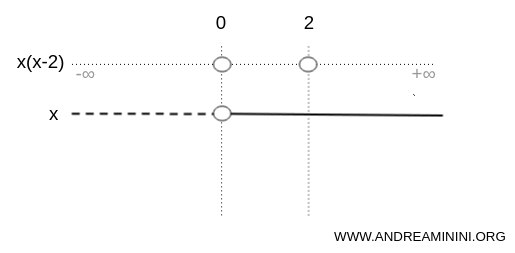
Nota. Nello schema grafico che sto usando la linea tratteggiata indica i valori negativi mentre la linea continua i valori positivi. Il cerchio indica il punto in cui l'espressione è uguale a zero. In alternativa alla linea tratteggiata o continua potrei anche indicare un solo segno meno per ogni intervallo negativo e un solo segno + per ogni intervallo positivo. E' una rappresentazione alternativa più sintetica ma il significato è sempre lo stesso.

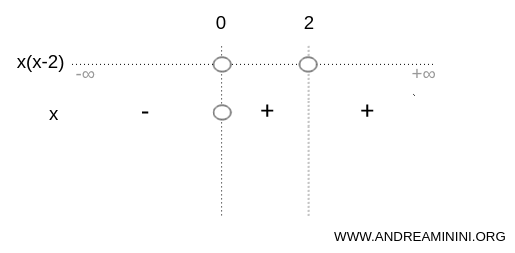
L'espressione (x-2) è negativa nell'intervallo (-∞;2), è uguale a zero nel punto x=2 ed è positiva nell'intervallo (2;+∞).

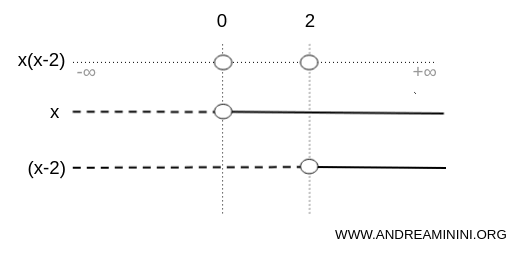
A questo punto applico la regola del segno per capire in quali intervalli il prodotto tra x e (x-2) è positivo.

Nell'intervallo (-∞;0) sia x che (x-2) sono negativi.

Quindi, per la regola algebrica del segno, quando due fattori hanno lo stesso segno il loro prodotto è positivo x·(x-2)>0

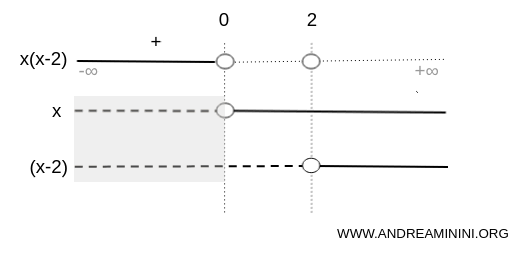
Nell'intervallo (0;2) il fattore x è positivo mentre il fattore (x-2) è negativo.

Quindi, per la regola algebrica del segno, quando due fattori hanno segno discorde, il loro prodotto è negativo x·(x-2)<0

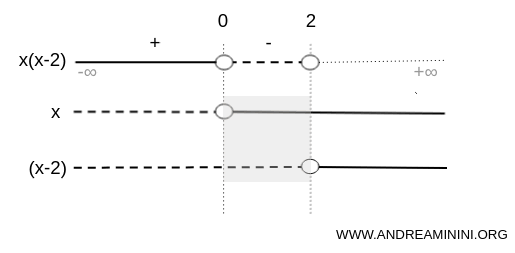
Nell'intervallo (2;+∞) sia x che (x-2) sono positivi.

Quindi, per la regola algebrica del segno, quando due fattori hanno lo stesso segno il loro prodotto è positivo x·(x-2)>0

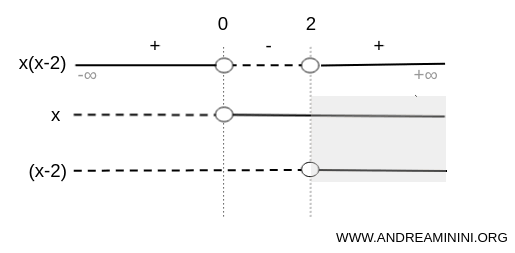
In conclusione la disequazione x(x-2)>2 è soddisfatta negli intervalli (-∞;0) e (2;+∞).

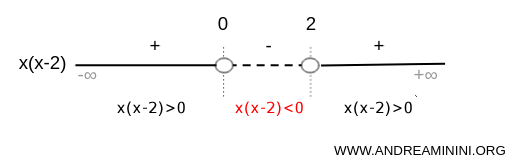
Per rappresentare graficamente l'insieme delle soluzioni della disequazione x(x-2)>0 traccio una linea continua nei punti in cui la disequazione è soddisfatta.

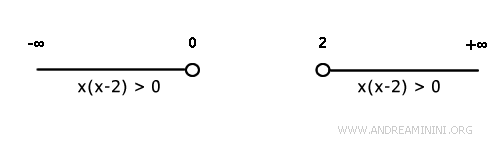
In alternativa alla rappresentazione grafica, per scrivere la soluzione posso usare la rappresentazione con intervalli dove indico i valori dell'incognita che soddisfano la disequazione.

$$ x \in \ ] \ -\infty \ ; \ 0 \ [ \ ∪ \ ] \ 2 \ ; \ +\infty \ [ $$

Dove il simbolo U è l'operatore di unione degli insiemi.

Nota. La parentesi quadra rivolta verso l'esterno vuol dire che l'estremo dell'intervallo non è incluso nella soluzione. Ad esempio, 0 e 2 non sono soluzioni. Equivale al cerchietto vuoto della rappresentazione grafica. Viceversa, la parentesi quadra rivolta verso l'interno indica che l'estremo dell'intervallo è incluso nella soluzione. Equivale al cerchietto pieno della rappresentazione grafica. In alternativa, per indicare che un estremo non è incluso nell'intervallo posso anche utilizzare le parentesi tonde. E' un'altra notazione matematica per indicare gli intervalli molto frequente. $$ x \in \ ( \ -\infty \ ; \ 0 \ ) \ ∪ \ ( \ 2 \ ; \ +\infty \ ) $$ In ogni caso, i simboli +∞ e -∞ vanno sempre considerati come estremi esclusi dall'intervallo perché non sono numeri.

Le condizioni di esistenza

Le condizioni di esistenza (spesso indicate con C.E.) sono le condizioni che le variabili della disequazione devono rispettare perché abbiano un significato.

Un esempio pratico

Questa disequazione

$$ \frac{x}{x-2} $$

esiste per qualsiasi valore reale della x ad eccezione che per il valore x=2.

Quando x=2 il denominatore è uguale a zero e nessun numero può essere diviso per zero.

Pertanto le condizioni di esistenza della disequazione sono

$$ x \in R - \{ 2 \} $$

ossia tutti i numeri dell'insieme dei numeri reali (R) tranne il numero 2.

Il grado della disequazione

Il grado della disequazione è il grado del polinomio della disequazione ossia l'esponente più alto della variabile incognita.

Un esempio pratico

Questa disequazione è di grado 1 perché l'esponente più alto dell'incognita è 1.

$$ x - 1 > 0 $$

Nota. Le disequazioni di primo grado sono anche dette disequazioni lineari.

Questa disequazione è di grado 2 perchè l'esponente più alto dell'incognita è 2.

$$ x^2 + x - 4 > 0 $$

Questa disequazione è di grado 3 perchè l'esponente più alto dell'incognita è 3

$$ 2x^3 - x + 1 > 0 $$

Tipi di disequazioni

La disequazione è detta

• intera
  se l'incognita compare solo al numeratore delle frazioni eventualmente presenti nella disequazione

  Esempio $$ x^2 + \frac{2x}{3} - 3 \gt 0 $$

• frazionaria o fratta
  se l'incognita compare anche al denominatore delle frazioni eventualmente presenti nella disequazione

  Esempio $$ x^2 + \frac{2}{3x} - 3 \gt 0 $$

• lineare
  se il grado della disequazione è uguale a 1 ossia se tutte le variabili incognite hanno un grado di esponente uguale a a 1.
  

  Esempio $$ 2x - 3 \gt 2y - 7 $$

• numerica
  se oltre all'incognita non ci sono altre lettere nella disequazione

  Esempio $$ x^2 + 3x - 3 \gt 0 $$

• letterale
  se oltre all'incognita ci sono altre lettere (costanti o parametri) nella disequazione

  Esempio $$ kx^2 + 3k - 3 \gt 0 $$

E così via.