Disequazione biquadratica
Una disequazione biquadratica è una disequazione di 4° che si presenta in questa forma $$ ax^4 \pm bx^2 \pm c \gt 0 $$ oppure $$ ax^4 \pm bx^2 \pm c \lt 0 $$ Dove il coefficiente a è diverso da zero a<>0.
Per risolvere queste disequazioni introduco una variabile incognita ausiliaria.
$$ t = x^2 $$
In questo modo la disequazione si trasforma in una disequazione di 2° grado ed è molto più semplice da risolvere.
$$ at^2 \pm bt + c > 0 $$
Dopo aver risolto la disequazione di 2° grado, sostituisco nella soluzione l'incognita t con x.
Un esempio pratico
Devo risolvere la disequazione di 4° grado
$$ 2x^4-7x^2-4 < 0 $$
E' una disequazione biquadratica con a≠0
Per risolverla introduco l'incognita ausiliaria t.
$$ t=x^2 $$
Sostituisco x con t nella disequazione e ottengo una disequazione di 2° grado equivalente
$$ 2t^2-7t-4 < 0 $$
A questo punto risolvo la disequazione di 2° grado studiando l'equazione associata.
$$ 2t^2-7t-4 = 0 $$
Si tratta di una parabola con la concavità rivolta verso l'alto.
Il determinante è positivo Δ=(-7)2-4·2·(-4)=81, quindi l'equazione 2t2-7t-4=0 ha due radici.
$$ t = \frac{-(-7) \pm \sqrt{(-7)^2 - 4 \cdot 2 \cdot (-4)}}{2 \cdot 2} $$
$$ t = \frac{7 \pm \sqrt{49 +32}}{4} $$
$$ t = \frac{7 \pm \sqrt{81}}{4} $$
$$ t = \frac{7 \pm 9}{4} = \begin{cases} t_1 = \frac{7-9}{4} = -\frac{1}{2} \\ \\ t_2 = \frac{7+9}{4} = 4 \end{cases} $$
Le radici dell'equazione associata sono t1=-1/2 e t2=4. Dove per convenzione t1<t2
Sapendo che la parabola è rivolta verso l'alto, assume valori positivi all'esterno dell'intervallo (t1,t2)=(-1/2,4)
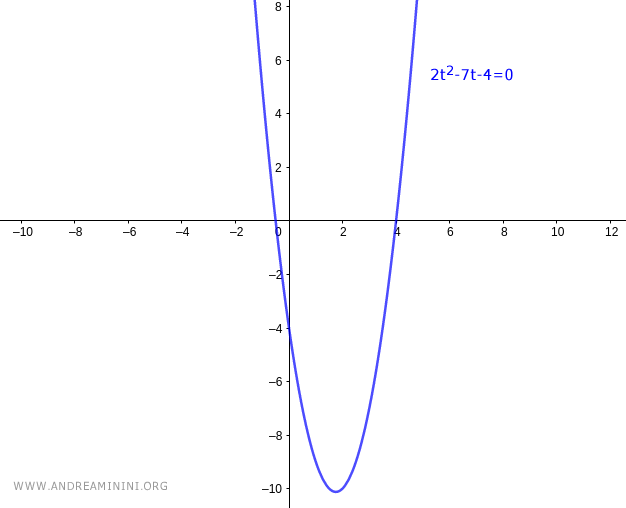
Quindi, la disequazione 2t2-7t-4<0 è soddisfatta nell'intervallo interno t∈(-1/2,4)
$$ - \frac{1}{2} < t < 4 $$
Una volta trovata la soluzione della disequazione di 2° grado, sostituisco la variabile ausiliaria t con x, sapendo che t=x2
$$ - \frac{1}{2} < x^2 < 4 $$
Nota. Dopo la sostituzione dell'incognita x è subito evidente che l'estremo inferiore è impossibile perché nessun numero reale al quadrato x2 ha come risultato un valore reale negativo (-1/2). Poiché sto cercando soluzioni reali, potrei già da adesso non considerare la prima relazione di minoranza e concentrarmi sulla seconda relazione x2<4.
Calcolo la radice quadrata di ogni membro per ricavare l'incognita x
$$ \sqrt{- \frac{1}{2}} < \sqrt{x^2} < \sqrt{4} $$
Non considero la prima radice perché ha il radicando negativo, quindi non ha soluzioni nell'insieme dei numeri reali.
Pertanto, l'incognita x deve avere valori compresi nell'intervallo x∈(-2,2)
$$ x < \pm 2 $$
ossia
$$ -2 < x < 2$$
Quest'ultima è la soluzione della disequazione biquadratica iniziale 2x4-7x2-4 < 0
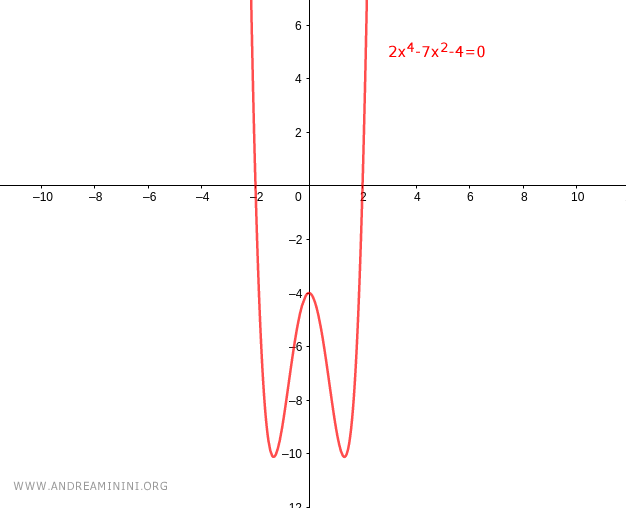
E così via.
