Le proprietà delle disuguaglianze numeriche
Le disuguaglianze numeriche soddisfano alcune proprietà.
Sono particolarmente utili perché consentono di semplificare la disuguaglianza e, quindi, agevolano la risoluzione dei problemi.
Proprietà additiva
Se addiziono o sottraggo uno stesso numero in entrambi i membri della disuguaglianza, ottengo un'altra disuguaglianza nello stesso verso.
$$ a < b \Leftrightarrow a + c < b + c $$
Esempio. Considero la disuguaglianza numerica $$ 4 > 2 $$ Addiziono +3 in entrambi i membri della disuguaglianza $$ 4 + 3 > 2 + 3 $$ $$ 7 > 5 $$ Il risultato è un'altra disuguaglianza nello stesso verso.
Esempio 2. Considero la stessa disuguaglianza precedente. $$ 4 > 2 $$ In questo caso sottraggo -5 in entrambi i membri. $$ 4 > 2 $$ $$ 4 - 5 > 2 - 5 $$ $$ - 1 > -3 $$ Anche in questo caso ottengo un'altra diseguaglianza nello stesso verso.
Proprietà moltiplicativa
Se moltiplico o divido entrambi i membri della disuguaglianza per uno stesso numero diverso da zero, ottengo un'altra disuguaglianza
- nello stesso verso se il numero è positivo (c>0)$$ a < b \Longleftrightarrow a \cdot c < b \cdot c $$
- nel verso contrario se il numero è negativo (c<0) $$ a < b \Longleftrightarrow a \cdot c > b \cdot c $$
Esempio. Considero la disuguaglianza numerica $$ 4 > 2 $$ Moltiplico per 3 entrambi i membri della disuguaglianza $$ 4 \cdot 3 > 2 \cdot 3 $$ $$ 12 > 6 $$ Il risultato è un'altra disuguaglianza nello stesso verso.
Esempio 2. Considero la disuguaglianza. $$ 16 > 8 $$ In questo caso divido per -2 entrambi i membri. $$ \frac{16}{-2} > \frac{8}{-2} $$ $$ -8 > -4 $$ Tuttavia, quest'ultima disuguaglianza è falsa (-8 non è maggiore di -4). Essendo -2 un numero negativo, devo anche invertire il verso della disuguaglianza. $$ -8 < -4 $$ Così facendo ottengo un'altra disuguaglianza vera (-8 è minore di -4) ma nel verso opposto rispetto a quella iniziale.
Perché la moltiplicazione o divisione per un numero negativo inverte il verso della disuguaglianza?
Considero due numeri reali positivi $a > 0$ e $b > 0$, con $a < b$.
Sulla retta reale, questo significa che il punto corrispondente ad $a$ si trova a sinistra rispetto al punto corrispondente a $b$.
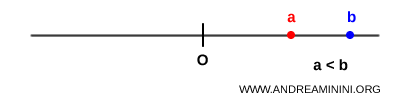
Se moltiplico entrambi i membri della disuguaglianza $a < b$ per $-1$, ottengo $ -a $ e $ -b $.
Questa operazione corrisponde a una simmetria rispetto all’origine $O$ della retta reale. In pratica, i punti di $a$ e $b$ si riflettono sul lato opposto rispetto allo zero.
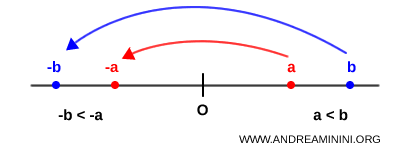
Quindi, dopo la simmetria il numero $-a$ si trova a destra di $-b$, perché $a < b$ implica $-a > -b $.
Di conseguenza, l’ordine tra i due numeri si inverte: ciò che era minore diventa maggiore, e viceversa.
Nota. La moltiplicazione o la divisione per -1 è un caso particolare di moltiplicazione o divisione per un numero negativo. In generale, moltiplicare o dividere entrambi i membri di una disuguaglianza per un numero negativo inverte il verso della disuguaglianza, perché si ribalta l’ordine relativo dei numeri sulla retta reale.
Proprietà dei reciproci dei numeri concordi
Dati due numeri concordi (con stesso segno) e diversi da zero, la diseguaglianza tra i loro reciproci ha verso contrario rispetto alla diseguaglianza tra i due numeri. $$ a > b \ \Longleftrightarrow \frac{1}{a} < \frac{1}{b} $$ La stessa proprietà non vale per i numeri discordi che, invece, mantengono lo stesso verso anche nei reciproci.
Esempio. Considero la diseguaglianza numerica $$ 4 > 2 $$ Sono due numeri concordi diversi da zero, quindi la diseguaglianza tra i loro reciproci ha verso contrario $$ \frac{1}{4} < \frac{1}{2} $$ Esempio 2. Considero quest'altra diseguaguaglianza $$ -4 < 2 $$ In questo caso i numeri hanno segno diverso, sono discordi, quindi i loro reciproci hanno lo stesso verso $$ - \frac{1}{4} < \frac{1}{2} $$
Dimostrazione
Per dimostrare questa proprietà considero due numeri $ a $ e $ b $ diversi da zero.
- Se i numeri hanno lo stesso segno, il loro prodotto è positivo $ ab > 0 $
- Se i numeri hanno il segno diverso, il loro prodotto è negativo $ ab < 0 $
Ora analizzo i due casi.
A] Numeri concordi
Poniamo che $ a > b $, essendo concordi il loro prodotto $ ab > 0 $ è positivo
Se divido entrambi i membri della diseguaglianza per un numero positivo, il verso non cambia $ \frac{a}{ab} > \frac{b}{ab} $.
$$ \frac{a}{ab} > \frac{b}{ab} \Rightarrow \frac{1}{b} > \frac{1}{a} \Rightarrow \frac{1}{a} < \frac{1}{b} $$
Il risultato finale è che la diseguaglianza tra i reciproci ha cambiato verso $ \frac{1}{a} < \frac{1}{b} $
A] Numeri discordi
Poniamo che $ a > b $, poiché sono discordi il loro prodotto è negativo $ ab < 0 $
Se divido entrambi i membri della diseguaglianza per un numero negativo il verso cambia $ \frac{a}{ab} < \frac{b}{ab} $.
$$ \frac{a}{ab} < \frac{b}{ab} \Rightarrow \frac{1}{b} < \frac{1}{a} \Rightarrow \frac{1}{a} > \frac{1}{b} $$
Il risultato finale è che la diseguaglianza tra i reciproci ha lo stesso verso $ \frac{1}{a} > \frac{1}{b} $
In questo modo ho dimostrato la regola sui reciproci, basandomi sulla proprietà che moltiplicare o dividere per un numero negativo inverte il verso di una disuguaglianza.
Potenza di disuguaglianze
Se elevo a $ n \in N $ due numeri non negativi, il verso della diseguaglianza non cambia. $$ a > b \Longleftrightarrow a^n > b^n $$ La stessa proprietà non vale per i numeri negativi.
Esempio. Considero la disuguaglianza numerica $$ 4 > 2 $$ Elevo entrambi i membri al quadrato e ottengo un'altra disuguaglianza con lo stesso verso $$ 4^2 > 2^2 \Rightarrow 16 > 4 $$ Esempio. Se uno o entrambi i numeri sono negativi, la regola non si può applicare perché il verso dipende dall'esponente $ n $ pari o dispari e dal valore assoluto dei termini. Ad esempio, se considero $ -4 < -2 $ ed elevo al quadrato il verso cambia $$ (-4)^2 < (-2)^2 \Rightarrow 16 > 4 $$. Se invece elevo al cubo il verso resta lo stesso. $$ (-4)^3 < (-2)^3 \Rightarrow -64 < -8 $$
Dimostrazione
Per dimostrare questa proprietà considero due numeri non negativi $ a>0 $ e $ b>0 $ diversi da zero in cui $ a>b $.
$$ a>b $$
Posso riscrivere $ a = ( b+ h ) $ dove $ h = a-b $
$$ b+h>b $$
Essendo $ a>b $ il termine $ h=a-b >0 $ è positivo.
Elevo entrambi i membri della disuguaglianza a $ n \in N $
$$ (b+h)^n>b^n $$
Se $ n = 2 $ (pari) espando il quadrato del binomio
$$ (b+h)^2>b^2 $$
$$ b^2 + 2bh + h^2 > b^2 $$
E' evidente che il primo membro è maggiore del secondo poiché $ b^2 $ appare in entrambi i lati della disuguaglianza e tutti gli altri termini sono positivi perché $ b>0 $ e $ h>0 $ sono positivi.
Se $ n = 3 $ (dispari) espando il cubo del binomio
$$ (b+h)^3>b^3 $$
$$ b^3 + 3hb^2 + 3bh^2 + h^3 > b^3 > b^3 $$
Anche in questo caso il primo membro è maggiore del secondo, perché $ b^3 $ appare in entrambi i lati della disuguaglianza e tutti i termini sono positivi perché $ b>0 $ e $ h>0 $ sono positivi.
Pertanto, quando i numeri $ a $ e $ b $ sono non negativi, se elevo per un numero naturale $ n \in N $, sia pari che dispari, entrambi i membri della disuguaglianza, il verso non cambia.
Addizione di disuguaglianze con lo stesso verso
Se sommo membro a membro due disuguaglianze con lo stesso verso, ottengo un'altra disuguaglianza con lo stesso verso. $$ a > b \ , \ c > d \ \Longleftrightarrow a+c > b +d $$ La stessa proprietà non vale per i numeri discordi.
Esempio. Considero le disuguaglianze numeriche $$ 4 > 2 $$ $$ 5 > 3 $$ Le due diseguaglianze hanno lo stesso verso. Sommo membro a membro le disuguaglianze $$ 4+5 > 2+3 $$ Il risultato è un'altra disuguaglianza con lo stesso verso $$ 9 > 5 $$
Prodotto di disuguaglianze con lo stesso verso tra numeri positivi
Se moltiplico membro a membro due disuguaglianze con lo stesso verso tra due numeri positivi, ottengo un'altra disuguaglianza nello stesso verso. $$ a > b \ , \ c > d \ \Longleftrightarrow a \cdot c > b \cdot d $$ La stessa proprietà non vale per i numeri negativi.
Esempio. Considero le disuguaglianze numeriche $$ 4 > 2 $$ $$ 5 > 3 $$ Le due diseguaglianze hanno lo stesso verso e i termini sono numeri positivi. Moltiplico membro a membro le disuguaglianze $$ 4 \cdot 5 > 2 \cdot 3 $$ Il risultato è un'altra disuguaglianza con lo stesso verso $$ 20 > 6 $$
E così via.
