Disequazione di primo grado

Le disequazioni di primo grado sono disequazioni del tipo $$ ax+b>0 $$ oppure $$ ax+b<0$$ Dove il coefficiente a≠0 è diverso da zero.

Il grado del polinomio della disequazione di 1° grado è pari a uno.

La potenza della variabile incognita ha esponente pari a uno.

Nota. La relazione d'ordine in una disequazione di primo grado può anche essere maggiore-uguale $$ ax + b \ge 0 $$ o minore-uguale $$ ax + b \le 0 $$

Un esempio pratico

Ho la disequazione

$$ 3x < 6 $$

E' una disequazione del 1° grado perché la variabile incognita (x) ha esponente uno.

Nota. La disequazione poteva essere scritta anche in forma normale. E' comunque la stessa disequazione. $$ 3x - 6 < 0 $$

Risolvere la disequazione vuol dire trovare i valori dell'incognita che soddisfano la relazione d'ordine.

Ricavo la variabile incognita (x) dividendo entrambi i membri per tre.

$$ \frac{3x}{3} < \frac{6}{3} $$

$$ x < 2 $$

Pertanto, l'insieme delle soluzioni (S) della disequazione di 1° grado è composto da tutti i numeri reali minori di 2.

$$ S = \{ \forall \ x \ \in R \ | \ x < 2 \} $$

ossia

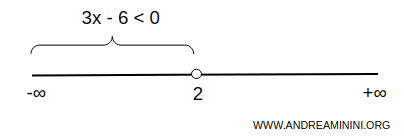
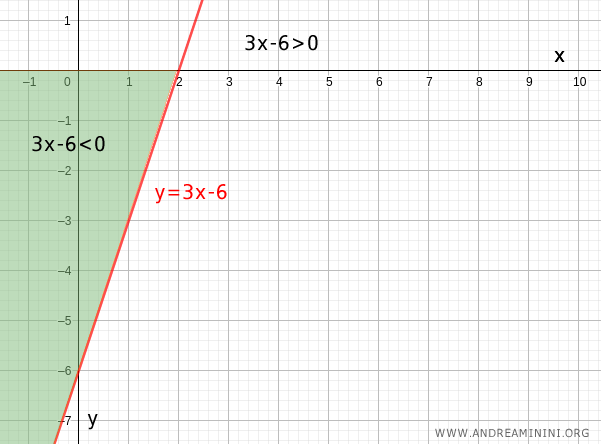
Nota. Allo stesso risultato si può arrivare anche facendo un'analisi grafica. La disequazione 2x-6<0 è associata all'equazione di una retta y=2x-6 detta equazione associata. La retta ha coefficiente angolare 2 e una intercetta sull'asse delle ordinate nel punto (0;-6). L'intersezione con l'asse dell'ascissa avviene, invece, nel punto (2;0). E' subito evidente che la retta assume valori minori di zero y=2x-6<0 in ogni punto dell'ascissa inferiore a x<2.

E così via.