Come risolvere una disequazione intera di secondo grado
Per risolvere una disequazione intera di secondo grado la riconduco alla sua forma normale $$ ax^2 + bx +c > 0 $$ oppure $$ ax^2 + bx +c > 0 $$ dove il primo coefficiente è diverso da zero a≠0
Nota. Se il primo coefficiente è negativo (a<0) potrei moltiplicare entrambi i membri della disequazione per (-1) e invertire la relazione d'ordine. Ad esempio, se la disequazione è la seguente $$ -5x^2+2x-3>0 $$ applico il secondo principio di equivalenza, moltiplico entrambi i membri per -1 e cambio il verso della disequazione $$ (-5x^2+2x-3) \cdot (-1) < 0 \cdot (-1) $$ $$ 5x^2-2x+3 < 0 $$ In questo modo semplifico i calcoli o perlomeno li rendo più intuitivi.
Una volta ricondotta alla forma normale, posso risolvere la disequazione usando il metodo della risoluzione algebrica o il metodo della risoluzione grafico.
Un esempio pratico
Esempo 1
Devo risolvere la disequazione di 2° grado
$$ -4x^2 +2x > 3 $$
La riconduco in forma normale
$$ -4x^2 +2x -3 > 0 $$
Risolvo l'equazione associata per vedere se esistono delle radici.
$$ -4x^2 +2x -3 = 0 $$
Il discriminante dell'equazione associata di 2° è negativo
$$ \Delta = b^2-4ac = (2)^2-4 \cdot (-4) \cdot (-3) = 4-48 = -44 $$
Quindi l'equazioni non ha radici.
La parabola è sempre al di sotto di zero perché il primo coefficiente è negativo (a=-4<0)
Ne consegue che la disequazione -4x2+2x-3>0 non è mai soddisfatta.
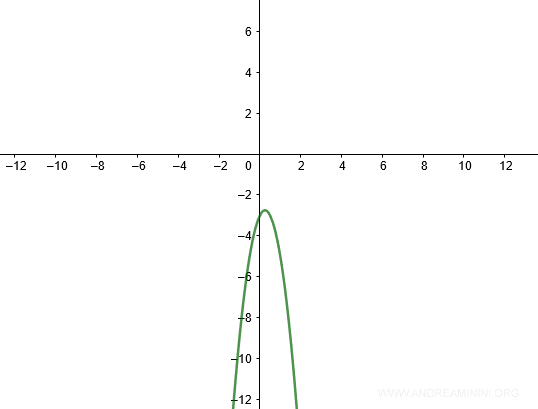
Esempo 2
Risolvo la disequazione precedente in un altro modo
$$ -4x^2 +2x > 3 $$
La riconduco in forma normale
$$ -4x^2 +2x -3 > 0 $$
Il primo coefficiente è negativo (a=-4).
Per semplificare i calcoli moltiplico entrambi i membri per -1 e inverto il verso della disequazione
$$ (-4x^2 +2x -3) \cdot (-1) < 0 \cdot (-1) $$
$$ 4x^2 -2x+3 < 0 $$
In questo modo ottengo una disequazione equivalente.
$$ 4x^2 -2x+3 = 0 $$
Risolvo l'equazione associata per vedere se esistono delle radici.
Il discriminante dell'equazione associata di 2° è negativo
$$ \Delta = b^2-4ac = (-2)^2-4 \cdot (4) \cdot (3) = 4-48 = -44 $$
Quindi l'equazioni non ha radici.
La parabola è sempre al di sopra di zero perché il primo coefficiente è positivo (a=4>0)
Ne consegue che la disequazione 4x2-2x+3<0 non è mai soddisfatta.
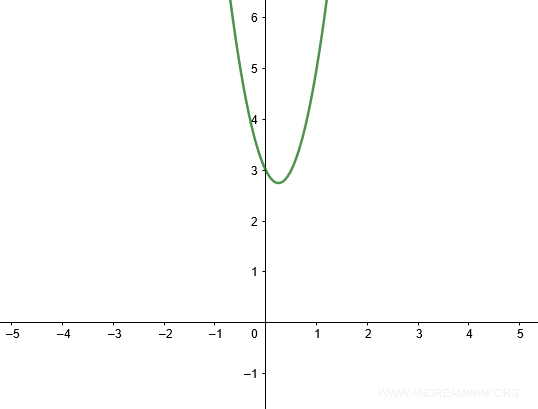
E così via.
