Disequazioni di secondo grado

Una disequazione di secondo grado di presenta in forma normale $$ ax^2+bx+c > 0 $$ oppure $$ ax^2+bx+c < 0 $$ Dove a,b,c sono coefficienti reali con a≠0.

Il grado del polinomio della disequazione di 2° grado è pari a due.

In pratica, la variabile incognita ha esponente uguale a due.

Nota. Le disequazioni di secondo grado possono essere scritte anche con la relazione d'ordine maggiore-uguale $$ ax^2+bx+c \ge 0 $$ oppure minore-uguale $$ ax^2+bx+c \le 0 $$

Come risolvere un'equazione di secondo grado

Devo trovare le soluzioni di una disequazione di 2° grado scritta in forma normale

$$ ax^2+bx+c > 0 $$

Considero l'equazione associata

$$ ax^2+bx+c = 0 $$

Poi individuo il tipo di parabola.

• a>0
  se il coefficiente a>0 la parabola ha la concavità rivolta verso l'alto.
• a<0
  se il coefficiente a<0 la parabola ha la concavità rivolta verso il basso.

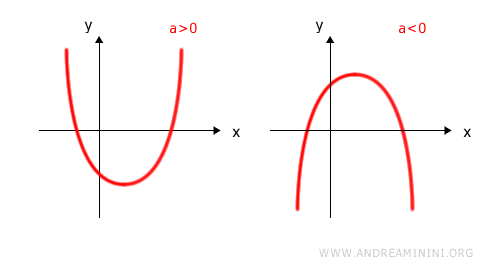
Nota. Questa prima distinzione è utile perché mi permette di capire se i valori più alti della parabola si trovano in un intervallo centrale oppure negli intervalli agli estremi.

Una volta capito l'orientamento della parabola, devo capire se l'equazione ha delle radici ossia dei punti x₁, x₂ in cui la curva interseca sull'asse dell'ascissa (x)

$$ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$$

Possono verificarsi tre casi

1] Il discriminante è positivo

Se il discriminante Δ = b²-4ac > 0 è positivo l'equazione ha due radici distinte x₁≠x₂.

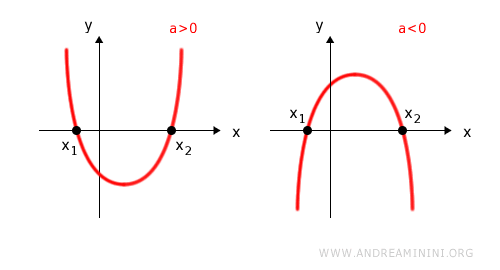
In questo caso la disequazione ha sicuramente delle soluzioni.

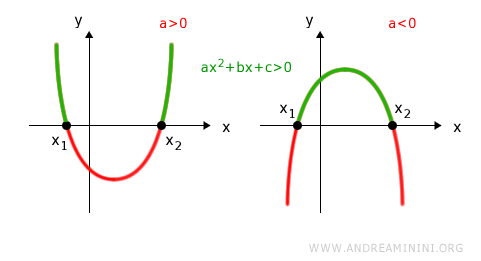
la disequazione ax²+bx+c>0 ha le seguenti soluzioni

1. nell'intervallo (-∞,x₁)∪(x₂,+∞) se la parabola è rivolta verso l'alto (a>0)
2. nell'intervallo (x_1:x₂) se la parabola è rivolta verso il basso (a<0)

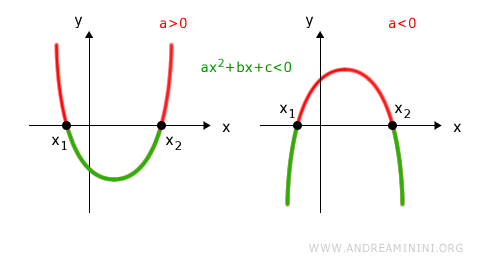
la disequazione ax²+bx+c<0 ha le seguenti soluzioni

3. nell'intervallo (x_1:x₂) se la parabola è rivolta verso l'alto (a>0)
4. nell'intervallo (-∞;x₁)∪(x₂;+∞) se la parabola è rivolta verso il basso (a<0)
   

2] Il discriminante è nullo

Se il discriminante Δ = b²-4ac = 0 è uguale a zero l'equazione ha due radici coincidenti x₁₌x₂.

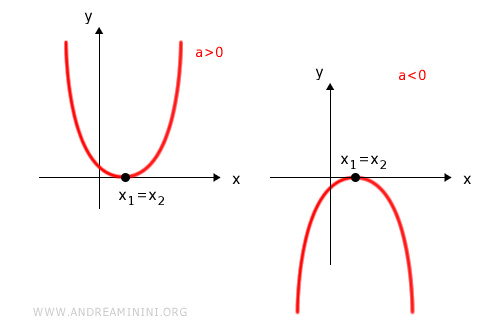
In questo caso la disequazione può avere infinite soluzioni o nessuna.

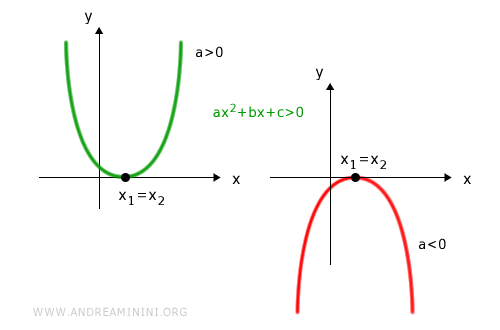
la disequazione ax²+bx+c>0 ha le seguenti soluzioni

1. nell'intervallo (-∞;x₁)∪(x₁;+∞) se la parabola è rivolta verso l'alto (a>0)
2. nessuna soluzione se la parabola è rivolta verso il basso (a<0)

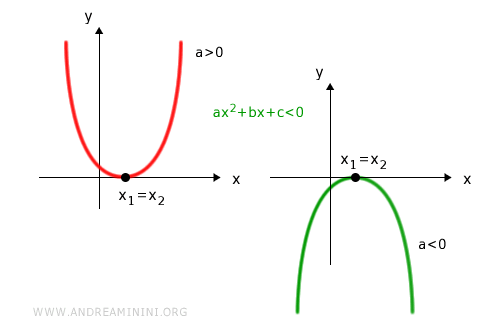
la disequazione ax²+bx+c<0 ha le seguenti soluzioni

3. nessuna soluzione se la parabola è rivolta verso l'alto (a>0)
4. nell'intervallo (-∞;x₁)∪(x_1;+∞) se la parabola è rivolta verso il basso (a<0)
   

3] Il discriminante è negativo

Se il discriminante Δ = b²-4ac < 0 è minore di zero l'equazione non ha radici

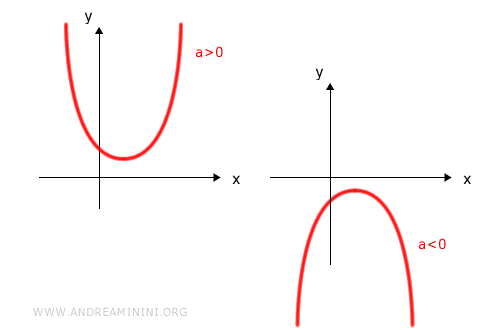
In questo caso la disequazione può avere infinite soluzioni o nessuna.

la disequazione ax²+bx+c>0 ha le seguenti soluzioni

1. infinite soluzioni nell'intervallo (-∞;+∞) se la parabola è rivolta verso l'alto (a>0)
2. nessuna soluzione se la parabola è rivolta verso il basso (a<0)

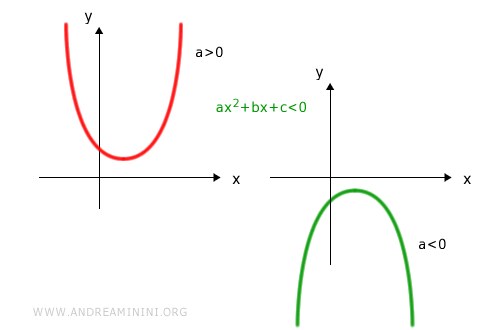
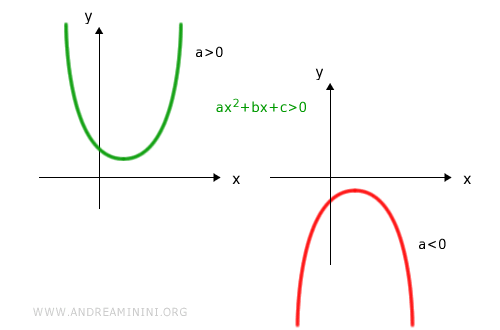
la disequazione ax²+bx+c<0 ha le seguenti soluzioni

3. nessuna soluzione se la parabola è rivolta verso l'alto (a>0)
4. infinite soluzioni nell'intervallo (-∞;+∞) se la parabola è rivolta verso il basso (a<0)
   

Un esempio pratico

Per risolvere la disequazione di 2° grado

$$ 2x^2 -x-1 < 0 $$

studio l'equazione associata

$$ 2x^2 -x-1 = 0 $$

Il coefficiente a=2 è maggiore di zero (a>0) quindi l'equazione è una parabola con la concavità rivolta verso l'alto.

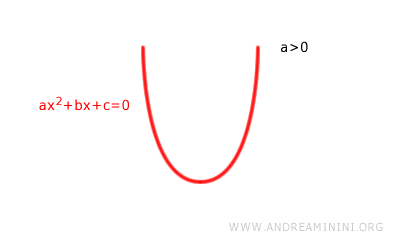
Nota. Non conosco ancora se la parabola interseca con l'asse dell'ascissa (x) oppure no. Per questa ragione non ho disegnato gli assi cartesiani. In questa fase quello che mi interessa sapere è soltanto l'orientamento della parabola verso l'alto o verso il basso.

A questo punto verifico se la parabola ha radici oppure no

Calcolo il discriminante dell'equazione associata

$$ \Delta = b^2 - 4ac = (-1)^2 - 4(2)(-1) = 1+8 = 9 $$

Il discriminante è positivo Δ>0

Pertanto l'equazione ha due radici distinte x₁ e x₂ ossia interse l'asse dell'ascissa in due punti diversi

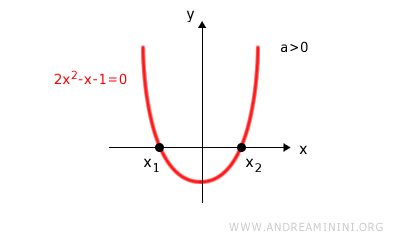
Poiché la parabola ha la concavità rivolta verso il basso, nell'intervallo interno tra le radici (x₁;x₂) l'equazione è minore di zero.

Quindi, le soluzioni della disequazione 2x²-x-1<0 esistono e sono comprese nell'intervallo interno (x₁;x₂)

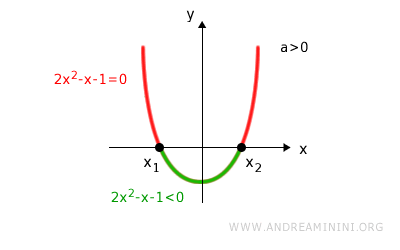
A questo punto, per conoscere l'intervallo (x₁;x₂) delle soluzioni devo calcolare le radici dell'equazione

$$ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$

$$ x = \frac{-(-1) \pm \sqrt{(-1)^2-4 \cdot (2) \cdot (-1)}}{2 \cdot (2)}= \frac{1 \pm \sqrt{9}}{4} = \frac{1 \pm 3}{4} $$

L'equazione ha due radici distinte x₁ e x₂

Per convenzione x₁ è sempre inferiore o uguale di x₂

$$ x = \begin{cases} x_1 = \frac{1-3}{4} = -\frac{1}{2} \\ \\ x_2 = \frac{1+3}{4} = 1 \end{cases} $$

Quindi, le soluzioni della disequazione sono comprese nell'intervallo

$$ (x_1 ; x_2 ) = ( - \frac{1}{2} ; 1 ) $$

Dal punto di vista grafico

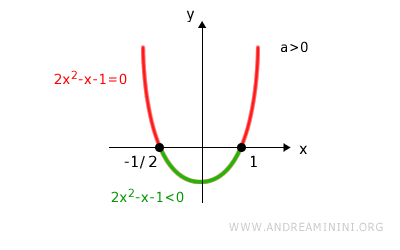
L'insieme delle soluzioni della disequazione è

$$ S = \{ \forall \ x \in R \ | \ - \frac{1}{2}<x<1 \} $$

Si legge "ogni x appartenente all'insieme dei numeri reali tale che x>-1/2 e x<1"

E così via.