Disequazioni irrazionali

Le disequazioni irrazionali sono disequazioni in cui la variabile incognita è l'argomento di una radice. $$ \sqrt[n]{a(x)} > b(x) $$ oppure $$ \sqrt[n]{a(x)} < b(x) $$

Quando in una disequazione l'incognita x è in un radicale occorre fare attenzione all'indice n della radice

Se n è dispari

La disequazione si risolve elevando alla potenza n-esima entrambi i membri

$$ \sqrt[n]{a(x)} > b(x) \ \ \ \text{equivale a} \ a(x) > b(x)^n $$

$$ \sqrt[n]{a(x)} < b(x) \ \ \ \text{equivale a} \ a(x) > b(x)^n $$

Se n è pari

La disequazione si risolve tramite un sistema equivalente

$$ \sqrt[n]{a(x)} > b(x) \ \ \ \text{equivale a} \begin{cases} a(x) \ge 0 \\ \\ b(x)<0 \end{cases} \cup \begin{cases} b(x) \ge 0 \\ \\ a(x)>b(x)^n \end{cases} $$ $$ $$ $$ \sqrt[n]{a(x)} < b(x) \ \ \ \text{equivale a} \begin{cases} a(x) \ge 0 \\ \\ b(x)>0 \\ \\ a(x)<b(x)^n \end{cases} $$

Un esempio pratico

In questo esempio considero la disequazione

$$ \sqrt{5-x} < x+1 $$

E' una disequazione irrazionale perché l'incognita x si trova anche in un radicale.

La radice quadrata ha indice n=2 pari e positivo.

Quindi, la disequazione non posso risolverla semplicemente elevando al quadrato entrambi i membri.

Per trovare la soluzione devo risolvere il sistema equivalente alla disequazione

$$ \begin{cases} a(x) \ge 0 \\ \\ b(x)>0 \\ \\ a(x)<b(x)^n \end{cases} $$

Sapendo che a(x)=5-x , b(x)=x+1 e n=2

$$ \begin{cases} 5-x \ge 0 \\ \\ x+1>0 \\ \\ 5-x<(x+1)^2 \end{cases} $$

$$ \begin{cases} x \le 5 \\ \\ x>-1 \\ \\ 5-x<x^2+2x+1 \end{cases} $$

$$ \begin{cases} x \le 5 \\ \\ x>-1 \\ \\ -x-x^2-2x<1-5 \end{cases} $$

$$ \begin{cases} x \le 5 \\ \\ x>-1 \\ \\ -3x-x^2<-4 \end{cases} $$

$$ \begin{cases} x \le 5 \\ \\ x>-1 \\ \\ x^2+3x>4 \end{cases} $$

Gli intervalli in cui sono verificate le singole disequazioni sono

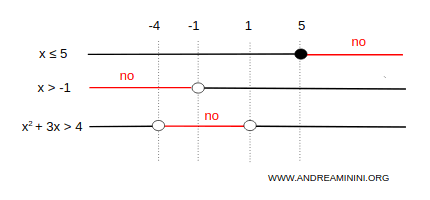
Nota. Lo studio delle prime due disequazioni x≤5 e x>-1 è banale. La disequazione $$ x^2+3x>4 $$ è invece una disequazione di 2° grado $$ x^2+3x-4>0 $$ Si tratta di una parabola con la concavità rivolta verso l'alto. Le radici sono $$ x = \frac{-3 \pm \sqrt{25}}{2} = \frac{-3 \pm 5}{2} = \begin{cases} x_1 = \frac{-3-5}{-2} = -4 \\ \\ x_2 = \frac{-3+5}{2} = 1 \end{cases} $$ Quindi la disequazione x²+3x-4>0 è soddisfatta nell'intervallo (-∞;-4)∪(1;∞)

Il sistema è risolto quando tutte le disequazioni sono soddisfatte.

In questo caso le disequazioni del sistema sono tutte soddisfatte nell'intervallo (1,5]

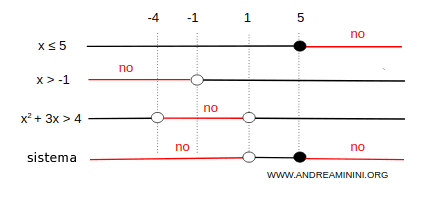
Pertanto, il sistema di disequazioni è risolto quando

$$ 1 < x \le 5 $$

Questa è anche la soluzione della disequazione iniziale

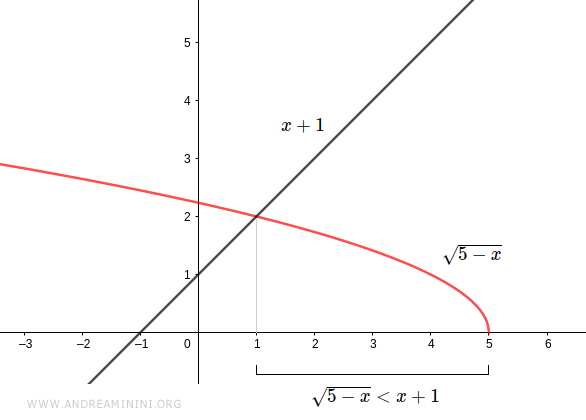
La dimostrazione

1] La disequazione ⁿ√a(x)>b(x) con indice n positivo pari

Ho una disequazione irrazionale con indice n positivo e pari

$$ \sqrt[n]{a(x)} > b(x) $$

Non conosco il valore di a(x), né quello di b(x).

Tuttavia, so per certo che una radice con indice pari non ammette un radicando negativo.

Quindi, la condizione di esistenza del radicando è a(x)≥0

$$ \begin{cases} \sqrt[n]{a(x)} > b(x) \\ \\ a(x) \ge 0 \end{cases} $$

Il termine b(x) può essere negativo, nullo o positivo.

Considero i casi separatamente

• Se b(x) ≥ 0 $$ \begin{cases} \sqrt[n]{a(x)} > b(x) \\ \\ a(x) \ge 0 \\ \\ b(x) \ge 0 \end{cases} $$ Sapendo che a(x) e b(x) sono entrambi non negativi, la diseguaglianza è soddisfatta solo quando a(x)>b(x)ⁿQuindi, l'insieme delle soluzioni è $$ S_1 = \begin{cases} a(x) \ge 0 \\ \\ b(x)>0 \\ \\ a(x)>b(x)^n \end{cases} $$ La condizione di esistenza a(x)≥0 posso anche eliminarla perchè è implicita nella condizione a(x)>b(x)ⁿ, in quanto la potenza b(x)ⁿ>0 è sempre positiva. $$ S_1 = \begin{cases} b(x)>0 \\ \\ a(x)>b^n \end{cases} $$
• Se b(x)<0$$ \begin{cases} \sqrt[n]{a(x)} > b(x) \\ \\ a(x) \ge 0 \\ \\ b(x)<0 \end{cases} $$ Sapendo che a(x) è positiva e b(x) è negativa, la diseguaglianza è sicuramente soddisfatta. Quindi, l'insieme delle soluzioni è $$ S_2 = \begin{cases} a(x) \ge 0 \\ \\ b(x)<0 \end{cases} $$

Pertanto, le soluzioni della disequazione iniziale appartengono all'unione degli insiemi S₁ e S₂

$$ S_1 \cup S_2 = \begin{cases} b(x)>0 \\ \\ a(x)>b(x)^n \end{cases} \cup \begin{cases} a(x) \ge 0 \\ \\ b(x)<0 \end{cases} $$

2] La disequazione ⁿ√a(x)<b(x) con indice n positivo pari

Ho una disequazione irrazionale con indice n positivo e pari

$$ \sqrt[n]{a(x)} < b(x) $$

Non conosco il valore di a(x), né quello di b(x).

Tuttavia, so per certo che una radice con indice pari non ammette un radicando negativo.

Quindi, la condizione di esistenza del radicando è a(x)≥0

$$ \begin{cases} \sqrt[n]{a(x)} < b(x) \\ \\ a(x) \ge 0 \end{cases} $$

Sapendo che (ax)≥0 è maggiore di zero, per essere soddisfatta la diseguaglianza anche b(x)>0 deve essere positivo.

Essendo sia a(x) che b(x) positivi, posso elevare entrambi i membri della disequazione alla potenza n-esima

Pertanto l'insieme delle soluzioni è

$$ S \ = \ \begin{cases} a(x) \ge 0 \\ \\ b(x)>0 \\ \\ a(x)<b(x)^n \end{cases} $$

E così via.