Disequazioni con valore assoluto
Per risolvere una disequazione in cui è presente il valore assoluto (modulo) della variabile incognita x $$ | P(x) | > Q(x) $$ devo eliminare il modulo trasformando la disequazione in una forma equivalente.
Ad esempio se la disequazione è nella forma
$$ |P(x)| > Q(x) $$
Per risolvere questo tipo di disequazioni
- Studio il segno dell'espressione P(x) all'interno del valore assoluto
- Una volta ottenuti gli intervalli in cui l'espressione P(x) è negativa, trasformo la disequazione in due sistemi di disequazioni.
- Il primo sistema per studiare il caso P(x)≥0. $$ \begin{cases} P(x) \ge 0 \\ \\ P(x) > Q(x) \end{cases} $$
- Il secondo sistema per studiare il caso P(x)<0 $$ \begin{cases} P(x) \lt 0 \\ \\ -P(x) > Q(x) \end{cases} $$ In questo caso si scrive -P(x) nella seconda disequazione per una proprietà del valore assoluto. Se P(x)<0 allora |P(x)|=-P(x).
- L'unione delle soluzioni dei due sistemi corrisponde alla soluzione della disequazione iniziale
Nota. In generale se k è un numero reale positivo k>0 qualsiasi $$ |P(x)| < k \Rightarrow -k < P(x) < k $$ $$ |P(x)| > k \Rightarrow -P(x) < -k ∨ P(x) > k $$
Un esempio pratico
Esempio 1
In questa disequazione l'incognita x è sotto modulo
$$ |3x-4| \ge 2x+5 $$
Studio il segno dell'espressione P(x)=x-4 dentro il valore assoluto
$$ 3x-4 \ge 0 $$
$$ x \ge \frac{4}{3} $$
L'espressione P(x)=x-4 è non negativa quando x≥4/3
A questo punto scrivo due sistemi, uno in cui x≥4/3 e l'altro in cui x<4/3
Il primo sistema
Se x≥4/3 il valore assoluto si può anche togliere
$$ \begin{cases} x \ge \frac{4}{3} \\ \\ 3x-4 \ge 2x+5 \end{cases} $$
$$ \begin{cases} x \ge \frac{4}{3} \\ \\ 3x-2x \ge 5+4 \end{cases} $$
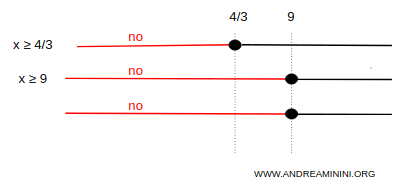
$$ \begin{cases} x \ge \frac{4}{3} \\ \\ x \ge 9 \end{cases} $$
Le soluzioni del primo sistema sono comprese nell'intervallo [9,+∞)
Il secondo sistema
Se x<4/3 per togliere il valore assoluto devo considerare l'opposto -P(x) dell'espressione P(x)
$$ \begin{cases} x < \frac{4}{3} \\ \\ -(3x-4) \ge 2x+5 \end{cases} $$
$$ \begin{cases} x < \frac{4}{3} \\ \\ -3x+4) \ge 2x+5 \end{cases} $$
$$ \begin{cases} x < \frac{4}{3} \\ \\ -2x-3x \ge +5-4 \end{cases} $$
$$ \begin{cases} x < \frac{4}{3} \\ \\ -5x \ge 1 \end{cases} $$
$$ \begin{cases} x < \frac{4}{3} \\ \\ -x \ge \frac{1}{5} \end{cases} $$
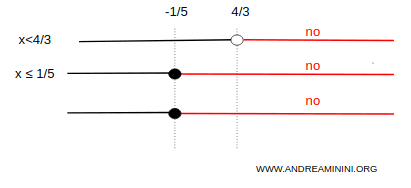
$$ \begin{cases} x < \frac{4}{3} \\ \\ x \le - \frac{1}{5} \end{cases} $$
Le soluzioni del primo sistema sono comprese nell'intervallo (-∞,-1/5]
L'unione delle soluzioni dei due sistemi corrisponde all'insieme delle soluzioni della disequazione iniziale
$$ ( -\infty, - \frac{1}{5} ] \cup [ 9 , + \infty) $$
Pertanto la disequazione è soddisfatta quando
$$ x \le - \frac{1}{5} \ ∨ \ x \ge 9 $$
Esempio 2
Devo risolvere la disequazione
$$ | 1-x| < 6 $$
In questo caso l'espressione dentro il modulo P(x)=1-x mentre Q(x)=6
Elimino il modulo trasformando la disequazione iniziale in due sistemi
$$ \begin{cases} P(x) \ge 0 \\ \\ P(x) < Q(x) \end{cases} \ \ \ \ \ \ \begin{cases} P(x) < 0 \\ \\ -P(x) < Q(x) \end{cases} $$
A questo punto risolvo i due sistemi
Il primo sistema
Risolvo il primo sistema sapendo che P(x)=1-x e Q(x)=6
$$ \begin{cases} P(x) \ge 0 \\ \\ P(x) < Q(x) \end{cases} $$
$$ \begin{cases} 1-x \ge 0 \\ \\ 1-x < 6 \end{cases} $$
$$ \begin{cases} -x \ge -1 \\ \\ -x < 6-1 \end{cases} $$
$$ \begin{cases} x \le 1 \\ \\ -x < 5 \end{cases} $$
$$ \begin{cases} x \le 1 \\ \\ x > -5 \end{cases} $$
Il primo sistema si risolve con qualsiasi valore x>-5 e x≤1 ossia x in (-5,1].
$$ x \in (-5, 1] $$
Il secondo sistema
Risolvo il secondo sistema sapendo che P(x)=1-x e Q(x)=6
$$ \begin{cases} P(x) < 0 \\ \\ -P(x) < Q(x) \end{cases} $$
$$ \begin{cases} 1-x < 0 \\ \\ -(1-x) < 6 \end{cases} $$
$$ \begin{cases} -x < -1 \\ \\ x-1 < 6 \end{cases} $$
$$ \begin{cases} x > 1 \\ \\ x < 6+1 \end{cases} $$
$$ \begin{cases} x > 1 \\ \\ x < 7 \end{cases} $$
Il secondo sistema si risolve con qualsiasi valore x>1 e x<7 ossia x in (1, 7).
$$ x \in (1, 7) $$
La soluzione della disequazione
La soluzione della disequazione iniziale è l'unione delle soluzioni dei due sistemi.
$$ x \in (-5, 1] \cup (1,7 ) $$
$$ x \in (-5, 7 ) $$
In altri termini, la soluzione è qualsiasi valore tra -5 e 7
$$ -5 < x < 7 $$
E così via
