Disequazioni fratte

Una disequazione fratta è una disequazione in cui l'incognita si trova al denominatore. $$ \frac{A(x)}{B(x)} >0 $$ oppure $$ \frac{A(x)}{B(x)} <0 $$

Come risolvere una disequazione fratta

Per risolvere questo tipo di disequazioni

1. Trasformo la disequazione in forma normale $$ \frac{A(x)}{B(x)} > k $$ $$ \frac{A(x)}{B(x)} -k > 0 $$
2. Impongo la condizione di esistenza che il denominatore B(x) sia non nullo $$ B(x) \ne 0 $$
3. Studio il segno del numeratore A(x) e del denominatore B(x)
4. Applico la regola dei segni per studiare il segno della frazione

Nota. Lo stesso vale se al posto delle relazioni di minore o maggiore si trovano le relazioni maggiore-uguale $$ \frac{A(x)}{B(x)} \ge 0 $$ o minore-uguale $$ \frac{A(x)}{B(x)} \le 0 $$.

Un esempio pratico

Esempio 1

Devo studiare questa disequazione fratta

$$ \frac{5x-1}{x-3} \ge 1 $$

Trasformo la disequazione nella forma normale portando tutti i termini a sinistra.

$$ \frac{5x-1}{x-3} -1 \ge 0 $$

$$ \frac{5x-1-(x-3)}{x-3} \ge 0 $$

$$ \frac{5x-1-x+3}{x-3} \ge 0 $$

$$ \frac{4x+2}{x-3} \ge 0 $$

Il denominatore non può essere nullo. Se lo fosse si verificherebbe una divisione per zero.

Quindi, impongo come condizione di esistenza della disequazione

$$ x-3 \ne 0 $$

$$ x \ne 3 $$

Per comodità scrivo il simbolo ∄ della non esistenza sul quadro dei segni che man mano andrò a compilare.

 

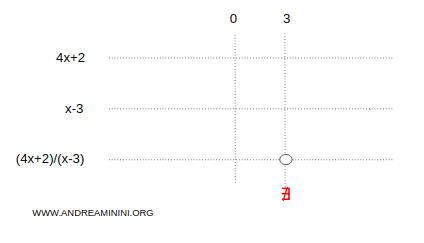
A questo punto studio il segno del polinomio al numeratore

$$ 4x+2 \ge 0 $$

$$ x \ge \frac{-2}{4} $$

$$ x \ge \frac{-1}{2} $$

Il numeratore è positivo per ogni x maggiore di -1/2

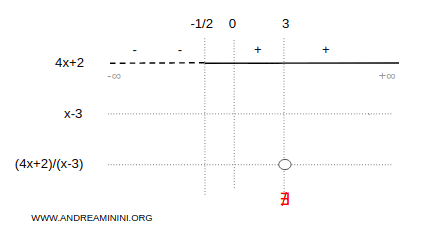
Poi studio il segno del denominatore

$$ x-3 \ge 0 $$

$$ x \ge 3 $$

Il denominatore è positivo per ogni x maggiore di 3.

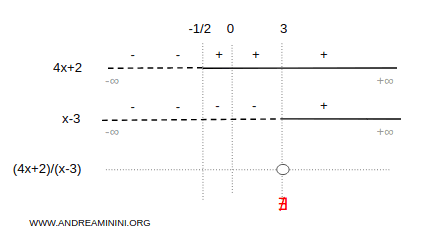
A questo punto applico la regola del segno tra i due risultati per studiare il segno della frazione.

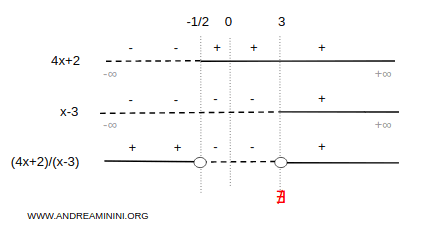
Pertanto, la disequazione iniziale è verificata negli intervalli (-∞, -1/2] e (3,+∞).

$$ x \le - \frac{1}{2} \ ∨ \ x \gt 3 $$

In questi intervalli la disequazione è maggiore o uguale a zero.

Esempio 2

Considero la disequazione fratta seguente:

\[ \frac{x - 3}{x + 2} > 1 \]

Sposto tutti i valori nel membro di sinistra

\[ \frac{x - 3}{x + 2} - 1 > 1 -1 \]

\[ \frac{x - 3}{x + 2} - 1 > 0 \]

Riscrivo il numero \( 1 \) come una frazione con denominatore \( x + 2 \):

\[ \frac{x - 3}{x + 2} - \frac{x + 2}{x + 2} > 0 \]

\[ \frac{x - 3 - (x + 2)}{x + 2} > 0 \]

\[ \frac{x - 3 - x - 2}{x + 2} > 0 \]

\[ \frac{-5}{x + 2} > 0 \]

In questo modo ho ottenuto una frazione con un unico denominatore e posso studiare il segno della frazione.

Per avere significato la frazione deve avere un denominatore non nullo.

\[ x+2 \ne 0 \]

\[ x+2 -2 \ne 0 -2 \]

\[ x \ne -2 \]

Quindi, il valore \( x = -2 \) è escluso perché annullerebbe il denominatore della frazione $ \frac{-5}{x + 2} > 0  $, rendendo l'espressione indefinita.

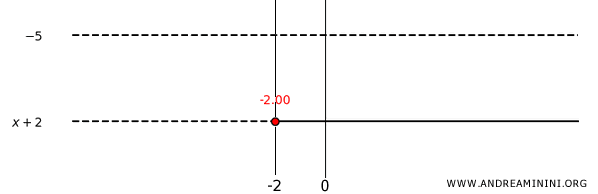
Una frazione è positiva quando numeratore e denominatore hanno lo stesso segno.

Poiché il numeratore è \( -5 \) è sempre negativo, la frazione $ \frac{-5}{x + 2} > 0  $ è maggiore di 0 quando anche il denominatore è negativo, cioè:

\[ x + 2 < 0 \]

\[ x < -2 \]

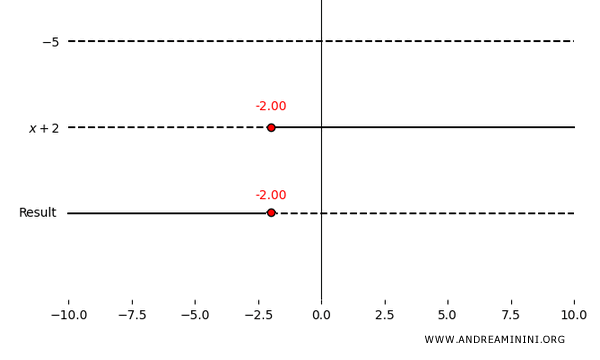
Quindi, l'unica possibilità affinché la frazione sia positiva è che il denominatore sia negativo, quindi la soluzione è:

\[ x < -2 \]

Escludendo il caso in cui \[ x = -2 \] in cui la frazione non è definita, la disequazione è positiva per ogni valore \( x <-2 \) ed è negativa per ogni valore \( x>-2 \).

Esercizi svolti

Ecco tre esercizi sulle disequazioni fratte suddivisi per livello di difficoltà, con la soluzione spiegata passo per passo.

• Esercizi base. Per comprendere il concetto delle disequazioni fratte e il dominio.
• Esercizi medi. Per affrontare disequazioni con polinomi di secondo grado.
• Esercizi avanzati. Per gestire parametri e condizioni complesse.

Esercizio 1 - Livello Base

Risolvo la seguente disequazione fratta:

\[ \frac{x + 2}{x - 3} > 0 \]

Per prima cosa trovo il dominio.

Il denominatore non può essere zero, quindi escludo \( x - 3 = 0 \Rightarrow x \neq 3 \).

Studio il segno della frazione. La frazione cambia segno nei punti in cui numeratore e denominatore si annullano:

• \( x + 2 = 0 \Rightarrow x = -2 \)
• \( x - 3 = 0 \Rightarrow x = 3 \) che è escluso

Costruisco la tabella dei segni.

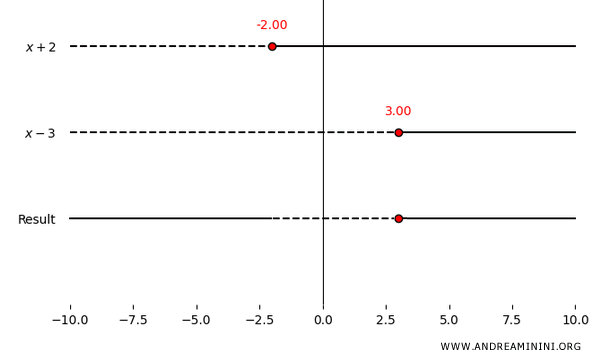
Per \( x < -2 \) il numeratore è negativo e il denominatore è positivo, quindi la frazione è negativa.

Per \( -2 < x < 3 \) il numeratore è positivo e il denominatore è positivo, quindi la frazione è positiva.

Per \( x > 3 \) il numeratore è positivo, il denominatore è negativo, quindi la frazione è negativa.

Pertanto, la soluzione è la seguente:

\[ x \in (-2, 3) \]

Escluso \( x = 3 \) perché si annulla il denominatore, la disequazione è positiva nell'intervallo (-2,3) ed è negativa altrove.

Esercizio 2 - Livello Medio

Risolvo la disequazione fratta

\[ \frac{x^2 - 4}{x^2 - x - 6} \leq 0 \]

Il numeratore posso riscriverlo come \( x^2 - 4 = (x - 2) \cdot (x + 2) \) che si annulla per \( x = \pm2 \).

\[ \frac{(x - 2) \cdot (x + 2)}{x^2 - x - 6} \leq 0 \]

Il denominatore posso fattorizzarlo come \( x^2 - x - 6 =  (x - 3) \cdot (x + 2) \)

\[ \frac{x^2 - 4}{(x - 3) \cdot (x + 2)} \leq 0 \]

Quindi, i punti in cui il denominatore si annulla sono \( x = 3 \) e \( x = -2 \). In questi due punti la frazione non è definita, perché si verifica una divisione per zero.

Ora studio il segno della frazione analizzando i singoli fattori.

Costruisco la tabella dei segni:

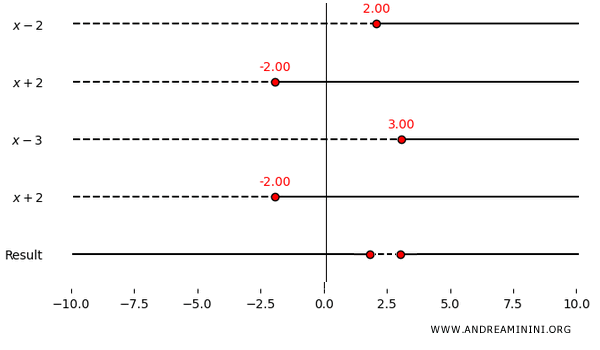
In questo caso, ad eccezione dei punti \( x=-2 \) e \( x=3 \) dove si annulla il denominatore, la disequazione è soddisfatta solo nell'intervallo \( (2,3) \) dove è negativa.

\[ (2,3) \]

Altrove la disequazione è positiva.

Esercizio 3 - Livello Avanzato

In questo esercizio devo risolvere la disequazione fratta seguente:

\[ \frac{x^2 - 3x + p}{x - 1} > 0 \]

Si tratta di una disequazione parametrica perché \( p \) è un parametro reale.

Per prima cosa studio il dominio della soluzione generale.

Il denominatore impone \( x - 1 \neq 0 \), quindi \( x \neq 1 \).

Al numeratore l'espressione \( x^2 - 3x + p \) è un trinomio di secondo grado.  Trovo le radici con la formula:

\[ x = \frac{3 \pm \sqrt{9 - 4p}}{2} \]

Perché il numeratore cambi segno, devo capire quando le soluzioni esistono ovvero \( 9 - 4p \geq 0 \).

$$ 9 - 4p \geq 0 $$

$$ - 4p \geq -9 $$

$$ (-1) \cdot - 4p \geq -9 \cdot (-1) $$

$$ 4p \leq 9 $$

$$ p \leq \frac{9}{4} $$

Quindi le soluzioni reali della disequazione esistono quando $ p \leq \frac{9}{4} $

A seconda del valore di \( p \), la disequazione avrà soluzioni differenti, da studiare caso per caso.

Il caso più semplice si ha quando \( p = 0 \), la tabella dello studio dei segni è la seguente:

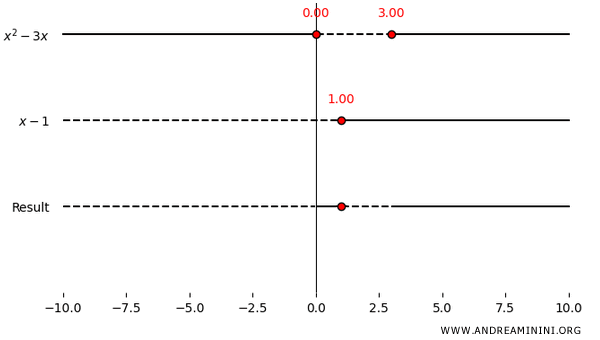
Nel caso particolare in cui \( p \ne 0 \) devo analizzare quando il numeratore è positivo.

\[ x^2 - 3x + p > 0 \]

In questo caso se $ p \leq \frac{9}{4} $ e $ p \ne 0 $ la disequazione si annulla in due punti distinti $ x_1 < x_2 $

\[ x = \frac{3 \pm \sqrt{9 - 4p}}{2} = \begin{cases} x_1 =  \frac{3 - \sqrt{9 - 4p}}{2} \\ \\ x_2 = \frac{3 + \sqrt{9 - 4p}}{2} \end{cases} \]

Poiché il segno di $ x^2 $ è positivo, la parabola è rivolta verso l’alto. Quindi il polinomio $ x^2 - 3x + p $ è negativo nell'intervallo (x_1, x_2) e positivo altrove $ ( -\infty, x_1) \cup ( x_2 , \infty ) $.

Considerando anche il denominatore \( x-1 \),

Intervallo	\( x < x_1 \)	\( x_1 < x < 1 \)	\( 1 < x < x_2 \)	\( x > x_2 \)
\( x^2 - 3x + p \) (Numeratore)	+	-	-	+
\( x - 1 \) (Denominatore)	-	-	+	+
Segno della frazione	-	+	-	+

In conclusione, la disequazione $ \frac{x^2 - 3x + p}{x - 1} > 0 $ è soddisfatta nell'intervallo seguente:

$$ (x_1 , 1 ) \cup ( x_2 , +\infty ) $$

E così via.