Il lato del decagono regolare è la sezione aurea del raggio
Il lato di un decagono regolare è la sezione aurea del raggio della circonferenza circoscritta $$ r : l = l : (r-l) $$
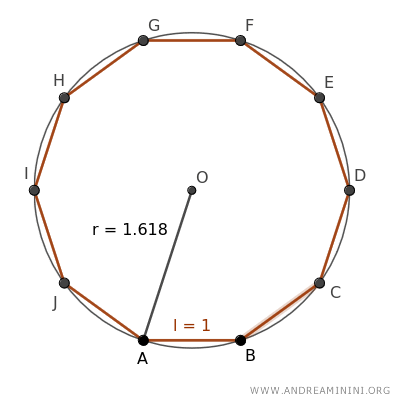
In altre parole, in un decagono regolare il rapporto tra il raggio della circonferenza circoscritta e il lato del decagono è uguale al numero aureo 1.618...
Un esempio pratico
Considero un decagono regolare con ogni lato di lunghezza pari a 1.
Il raggio della circonferenza circoscritta al decagono ha il raggio uguale a 1.618... ovvero al numero aureo.

Il segmento AK è congruente con il lato AB, quindi ha lunghezza pari a 1.
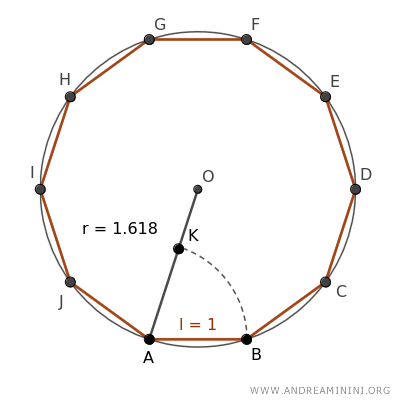
A questo punto verifico se è soddisfatta la proporzione della sezione aurea.
$$ \overline{AB} : \overline{AK} = \overline{AK} : \overline{OK} $$
Sapendo che OK=1 e AB=1.618...
$$ 1.618 : 1 = 1 : \overline{OK} $$
Il segmento OK è congruente con la differenza tra i segmenti OA-OK ovvero 1.618-1=0.618
$$ 1.618 : 1 = 1 : 0.618 $$
Svolgo le due divisioni e ottengo lo stesso risultato
$$ 1.618 = 1.618 $$
La proporzione è soddisfatta, pertanto il lato (AB) del decagono è la sezione aurea del raggio (OA) della circonferenza circoscritta.
Dimostrazione
Costruisco un decagono regolare, un poligono con 10 lati congruenti.
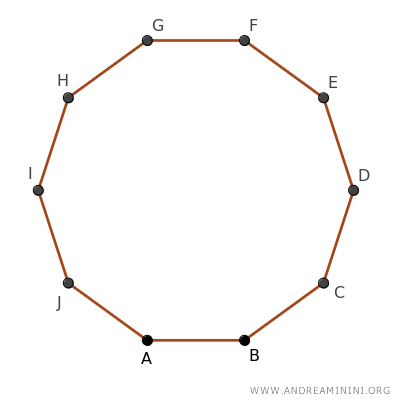
Tutti i poligoni regolari sono circoscrivibili.
Quindi, identifico il centro del decagono al fine di tracciare la circonferenza circoscritta al poligono, avente come centro il punto O e come raggio la lunghezza r.
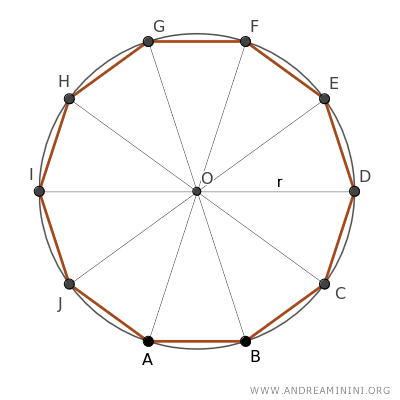
In questo modo ho suddiviso il decagono in 10 triangoli congruenti, perché secondo il terzo criterio di congruenza dei triangoli hanno tutti tre lati congruenti.
$$ ABO \cong BCO \cong CDO \cong ... $$
Tutti i triangoli hanno l'angolo al vertice O pari a 36° perché l'angolo giro (360°) è stato diviso in 10 parti congruenti.
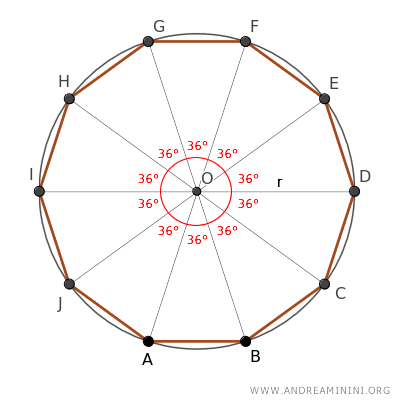
Continuo l'analisi sul triangolo ABO, poiché le proprietà dimostrate su un solo triangolo tra questi si applicano anche a tutti gli altri triangoli, grazie alla loro congruenza.
Il triangolo ABO è un triangolo isoscele perché ha due lati obliqui congruenti AO≅AB al raggio della circonferenza.
Essendo un triangolo isoscele, ha due lati congruenti alla base α≅β
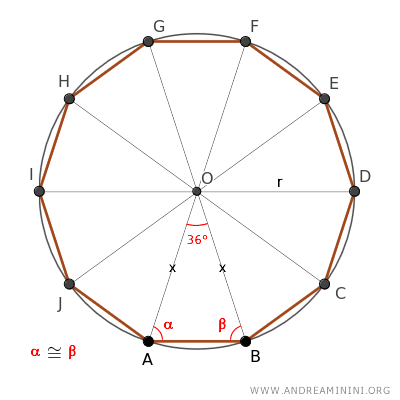
La somma degli angoli interni di un triangolo qualsiasi è sempre pari a 360°
$$ \alpha + \beta + 36° = 180° $$
Pertanto, deduco che la somma degli angoli α+β è uguale alla differenza tra 360°-36°
$$ \alpha + \beta = 180° - 36° $$
$$ \alpha + \beta = 144° $$
Sapendo che α≅β sono congruenti e la loro somma è α+β=144°, deduco che ciascun angolo ha un'ampiezza pari alla metà di 144°, ovvero α=72° e β=72°.
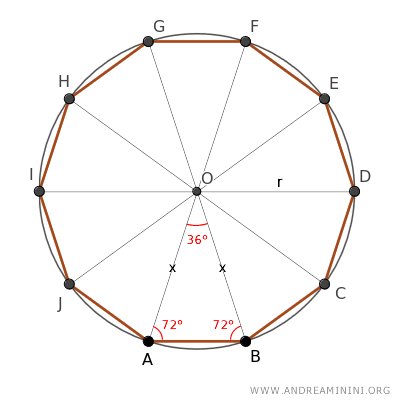
A questo punto traccio la bisettrice di uno degli angoli adiacenti alla base del triangolo ABO, che divide l'angolo (72°) in due angoli congruenti di 36°.
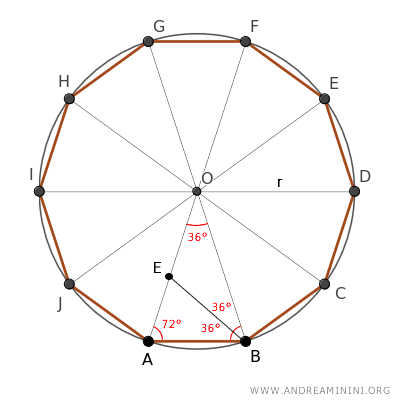
Il triangolo BOE è un altro triangolo isoscele, perché ha due angoli congruenti (36°) adiacenti alla base OB.
Pertanto, i lati obliqui OE≅BE sono congruenti.
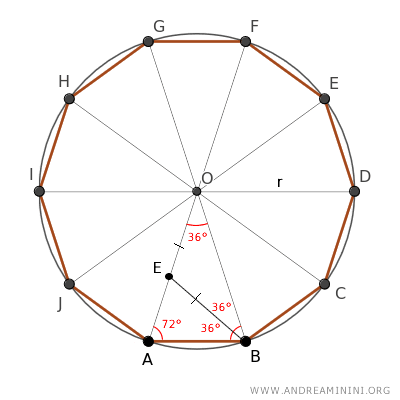
Osservando l'altro triangolo ABE mi accorgo che conosco già due angoli su tre, quindi posso dedurre per differenza anche l'ampiezza dell'ultimo angolo ovvero 180°-72-36°=72°
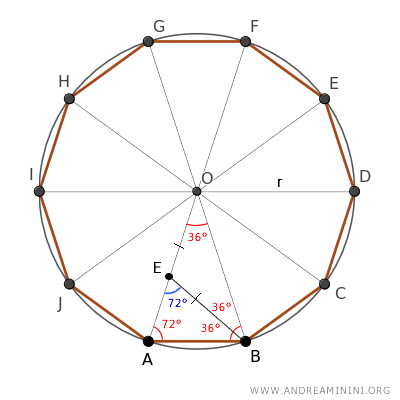
Pertanto, anche il triangolo ABE è un triangolo isoscele perché ha due angoli congruenti (72°) adiacenti a un lato
Di conseguenza, essendo isoscele, ha i lati obliqui congruenti AB≅BE
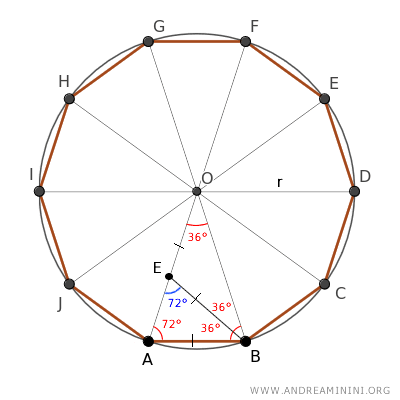
Di conseguenza, sapendo che AB≅EB e EB≅OE deduco che anche i segmenti AB≅OE sono congruenti.
I triangoli ABO e ABE sono triangoli simili, perché secondo il primo criterio di similitudine dei triangoli hanno due angoli congruenti (36°, 72°).
$$ ABO \aprox ABE $$
Pertanto, essendo simili, i triangoli ABO e ABE hanno i lati omologhi proporzionali.
$$ \overline{OB} : \overline{AB} = \overline{AB} : \overline{EA} $$
Sapendo che OB è il raggio (r) della circonferenza e AB è il lato (l) del poligono.
$$ r : l = l : \overline{EA} $$
Il segmento EA è uguale alla differenza OA-OE.
$$ \overline{EA} = \overline{OA} - \overline{OE} $$
Dove OA è il raggio mentre OE≅AB è congruente con il lato (l) AB del decagono.
$$ \overline{EA} = r - l $$
Quindi, il segmento EA è la differenza tra il raggio e il lato del decagono.
$$ r : l = l : \overline{EA} $$
$$ r : l = l : r - l $$
Questo dimostra che in un decagono il raggio (r) della circonferenza circoscritta sta al lato (l) del decagono, come il lato (l) sta alla differenza tra il raggio e il lato.
Di consequenza, il segmento (l) è il medio proporzionale tra il segmento (r) e la differenza (r-l) ovvero è la sezione aurea del segmento r.
E così via.
