La sezione aurea
La sezione aurea di un segmento quella parte del segmento che ha una proporzione speciale, è' medio proporzionale tra la lunghezza dell'intero segmento e quella della parte rimanente del segmento stesso.
La sezione aurea è anche nota come proporzione aurea, numero aureo, o Phi (simboleggiata come φ).
E' un rapporto matematico particolare che si incontra spesso in natura, nell'arte, nell'architettura ecc.
Nota. Gli antichi greci consideravano la sezione aurea come il simbolo dell'armonia tra le misure. Le proporzioni che rispettano questa regola sono spesso percepite come armoniose e gradevoli alla vista. Molti aspetti in natura si avvicinano alla sezione aurea. Ad esempio, le proporzioni del corpo umano, la forma delle conchiglie, ecc. Per questa ragione è stata utilizzata di frequente anche nell'arte e nell'architettura. Ad esempio, nella costruzione del Partenone di Atene, nell'Uomo Vitruviano di Leonardo da Vinci, ecc.
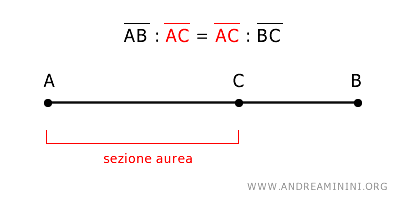
Ad esempio, considero un segmento AB e lo divido in due parti AC e BC.
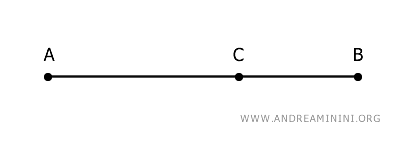
Il segmento AC è la sezione aurea del segmento se soddisfa questa proporzione:
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{BC} $$
In questo caso, il segmento AC è il medio proporzionale tra la lunghezza dell'intero segmento AB e la lunghezza del resto del segmento BC.
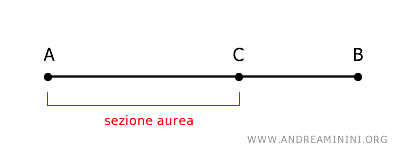
Il rapporto tra la sezione aurea AC e l'intero segmento è una costante 0.618033988749895
$$ \frac{ \overline{AC} }{ \overline{AB} } = 0.618033988749895 $$
Il rapporto tra l'intero segmento AB e la sezione AC, invece, è 1.618033988749895 ed è detto numero aureo (φ)
$$ \frac{ \overline{AB} }{ \overline{AC} } = 1.618033988749895 = φ $$
Quindi, per trovare la lunghezza della sezione aurea in un segmento, basta moltiplicare quella dell'intero segmento AB per una costante che approssimo per semplicità a 0.618
$$ \overline{AC} = 0.618 \cdot \overline{AB} $$
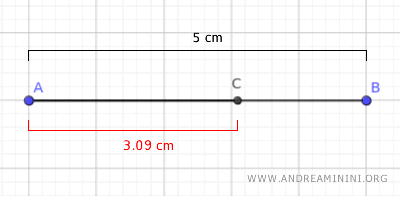
Ad esempio se un segmento AB ha una lunghezza pari a 5 cm.
La lunghezza della sezione aurea AC è 0.618·5 cm = 3.09 cm
$$ \overline{AC} = 0.618 \cdot 5 \ cm = 3.09 \ cm $$
Come si ottiene il numero 0.618? Per ottenerlo algebricamente basta considerare un segmento di un lunghezza unitaria AB=1 e la lunghezza della sezione aurea come incognita x. $$ 1 : x = x : (1-x) $$ Applico la proprietà fondamentale delle proporzioni $$ x \cdot x= 1 \cdot (1-x) $$ $$ x^2 = 1-x $$ $$ x^2 + x -1 = 0 $$ A questo punto risolvo l'equazione di secondo grado. $$ x = \frac{-1 \pm \sqrt{1^2-4 \cdot 1 \cdot -1}}{2} $$ $$ x = \frac{-1 \pm \sqrt{5}}{2} = \begin{cases} \frac{-1 - \sqrt{5}}{2} = \ non \ accettabile \\ \\ \frac{-1 + \sqrt{5}}{2} = 0.618033 \end{cases} $$
Come trovare la sezione aurea di un segmento
Considero un segmento AB.

Individuo il suo punto medio M e traccio un segmento perpendicolare sull'estremo B.
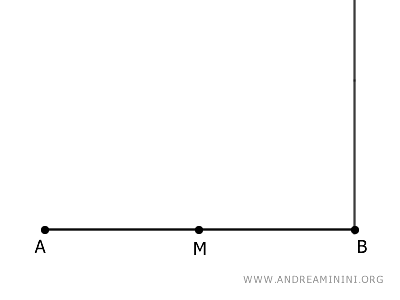
Centro il compasso sul punto B e con un'apertura BM disegno un arco che interseca il segmento perpendicolare nel punto C.
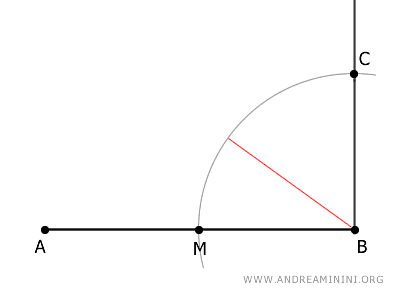
Traccio il segmento AC.
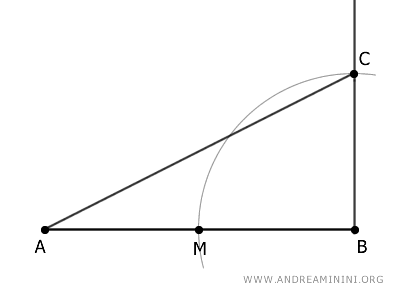
Poi centro il compasso sul punto C e con un'apertura CB traccio un altro arco che interseca il segmento AC nel punto D.
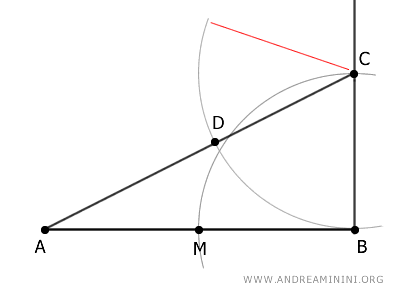
A questo punto, centro il compasso sul punto A e con un'apertua AD disegno un terzo arco che interseca il segmento AB nel punto E.
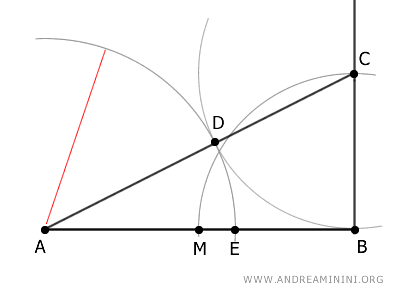
Il segmento AE è la sezione aurea del segmento AB.
La dimostrazione
Per dimostrare il segmento aureo considero il disegno fatto per la costruzione del segmento aureo AE.
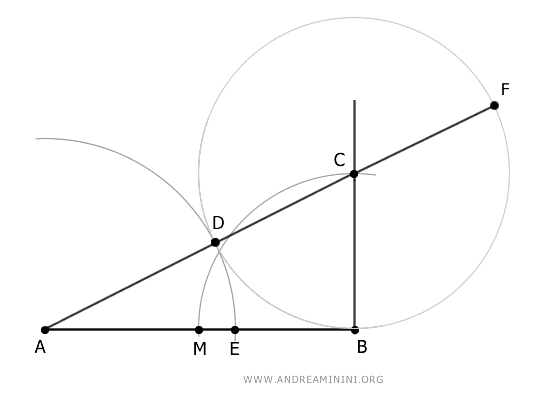
Il segmento AB è la tangente della circonferenza con centro C mentre il segmento AF è la secante.
Per il teorema della secante e la tangente, tra questi segmenti sussiste una relazione di proporzionalità.
$$ \overline{AF} : \overline{AB} = \overline{AB} : \overline{AD} $$
Applico la proprietà della scomposizione di una proporzione.
$$ ( \overline{AF} - \overline{AB} ) : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AD} $$
La circonferenza ha un raggio OB ≅ BM, quindi il diametro della circonferenza CE≅AB è congruente con il segmento AB.
$$ ( \overline{AF} - \overline{CE} ) : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AD} $$
Sapendo che AF-CE è il segmento AD
$$ \overline{AD} : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AD} $$
A sua volta il segmento AD≅AE è congruente con la sezione aurea AE.
$$ \overline{AE} : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AE} $$
Quindi, AB-AD è congruente con AB-AE
$$ \overline{AE} : \overline{AB} = ( \overline{AB} - \overline{AE} ) : \overline{AE} $$
La differenza AB-AE≅EB restituisce il resto del segmento AB dopo il segmento aureo AE.
$$ \overline{AE} : \overline{AB} = \overline{EB} : \overline{AE} $$
Infine, applico la proprietà del permutare delle proporzioni.
$$ \overline{AB} : \overline{AE} = \overline{AE} : \overline{EB} $$
Questo dimostra che il segmento AB sta alla sezione aurea AE come quest'ultima sta al resto del segmento EB.
Pertanto, il segmento AE è la sezione aurea del segmento AB.
Il rettangolo aureo
Il rettangolo aureo è un rettangolo in cui il rapporto tra il lato maggiore e quello minore è uguale al numero aureo φ=1.618...
Ad esempio, questo rettangolo è un rettangolo aureo.
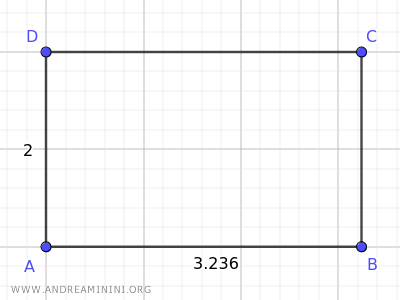
Il rapporto tra la lunghezza del lato maggiore (3.235) e quella del lato minore (2) è approssimativamente uguale al numero aureo (1.618).
$$ \frac{ \overline{AB} }{ \overline{AD} } = \frac{3.236}{2} = 1.618 $$
Se da un rettangolo aureo tolgo il quadrato costruito dal lato minore, ottengo un altro rettangolo aureo.
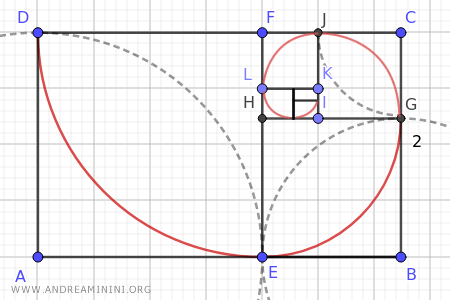
Questa combinazione di rettangoli aurei, ricavati uno dentro l'altro, genera una curva a spirale che si trova in molti molluschi in natura ed è utilizzata anche in diverse opere d'arte dell'uomo.
E così via.
