Numero aureo
Il numero aureo è approssimativamente il numero irrazionale $$ φ=1.6180339887... $$
Spesso viene rappresentato dalla lettera greca φ (phi).
E' un numero irrazionale che ha affascinato matematici, artisti e architetti per molti secoli a causa delle sue proprietà e del suo presunto legame con l'estetica e l'armonia naturale.
Nota. In passato si pensava che le proporzioni definite dal numero aureo siano particolarmente gradevoli alla vista. Questo ha portato alla sua applicazione in varie discipline, dalla pittura e la scultura all'architettura. Ad esempio, il Partenone ad Atene incarna le proporzioni del numero aureo, così come molte opere d'arte rinascimentali. In molti testi si parla anche di fenomeni naturali che tendono al numero aureo (es. la forma a spirale della conchiglia Nautilus) ma alcune delle sue presunte apparizioni in natura sono probabilmente sovrastimate.
Come si ottiene?
Il numero aureo si ottiene considerando due segmenti, \(a\) e \(b\), con \(a > b\), tali che il rapporto tra la somma dei due segmenti (\(a + b\)) e il segmento più lungo (\(a\)) sia uguale al rapporto tra il segmento più lungo (\(a\)) e quello più corto (\(b\)). In formula, questo si esprime come:
$$ \frac{a + b}{a} = \frac{a}{b} = \phi $$
Questa relazione produce un valore di:
$$ \phi = \frac{1 + \sqrt{5}}{2} \approx 1.6180339887... $$
La dimostrazione
Provo a spiegare perché il rapporto tra il segmento più lungo "a" e quello più corto "b" è uguale a 1.618...
$$ \phi = \frac{1 + \sqrt{5}}{2} \approx 1.6180339887... $$
Per farlo comincio dalla relazione tra i due segmenti come ipotesi di partenza.
$$ \frac{a + b}{a} = \frac{a}{b} = \phi $$
Il rapporto tra la somma dei due segmenti (\(a + b\)) e il segmento maggiore \(a\) è uguale a \(\phi\).
$$ \frac{a + b}{a} = \phi $$
Anche il rapporto tra il segmento maggiore \(a\) e il segmento minore \(b\) è uguale a \(\phi\).
$$ \phi = \frac{a}{b} $$
Da quest'ultima deduco che il segmento "b" è uguale al rapporto $ \frac{a}{ \phi } $
$$ b = \frac{a}{ \phi } $$
A questo punto considero solo la prima parte della relazione.
$$ \frac{a + b}{a} = \phi $$
Sapendo che \( b = \frac{a}{ \phi } \).
$$ \frac{a + \frac{a}{\phi}}{a} = \phi $$
Semplifico l'equazione dividendo entrambi i membri per \(a\).
$$ 1 + \frac{1}{\phi} = \phi $$
Questa equazione posso riscriverla in questa forma.
$$ \frac{1}{\phi} = \phi - 1 $$
Ora moltiplico entrambi i membri per \(\phi\) e, in questo modo, ottengo un'equazione quadratica in \(\phi\):
$$ 1 = \phi^2 - \phi $$
Riarrangiando i termini in questa forma.
$$ \phi^2 - \phi - 1 = 0 $$
Questa è un'equazione quadratica che posso risolvere usando la formula per le equazioni quadratiche.
$$ \phi = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Dove \(a = 1\), \(b = -1\), e \(c = -1\). Sostituendo questi valori nella formula, ottengo:
$$ \phi = \frac{-(-1) \pm \sqrt{(-1)^2 - 4(1)(-1)}}{2(1)} = \frac{1 \pm \sqrt{1 + 4}}{2} = \frac{1 \pm \sqrt{5}}{2} $$
Dato che \(\phi\) è un rapporto positivo, uso il segno \(+\), il che mi dà:
$$ \phi = \frac{1 + \sqrt{5}}{2} \approx 1.6180339887... $$
Questa spiegazione mostra come la relazione conduca direttamente al valore del numero aureo (1.618...) attraverso semplici passaggi algebrici e l'uso della formula per risolvere le equazioni quadratiche.
Un esempio pratico
Il numero aureo è strettamente legato alla successione di Fibonacci, una sequenza in cui ogni numero è la somma dei due precedenti (0, 1, 1, 2, 3, 5, 8, 13, 21, ...).
$$ \sigma = 0 \ , \ 1 \ , \ 1 \ , \ 2 \ , \ 3 \ , \ 5 \ , \ 8 \ , \ 13 \ , \ 21 \ , \ 34 \ , \ ... $$
Il rapporto tra numeri successivi nella sequenza di Fibonacci tende al numero aureo man mano che ci si sposta verso numeri più alti.
$$ \frac{1}{1} \ , \ \frac{2}{1} \ , \ \frac{3}{2} \ , \ \frac{5}{3} \ , \ \frac{8}{5} \ , \ \frac{13}{8} \ , \ \frac{21}{13} \ , \ \ \frac{34}{21} \ , \ ... $$
Calcolo i relativi quozienti
$$ 1 \ , \ 2 \ , \ 1.5 \ , \ 1.666 \ , \ 1.6 \ , \ 1.625 \ , \ 1.615 \ , \ 1.619 \ , \ ... $$
Osservazioni
Alcune note a margine sul numero aureo.
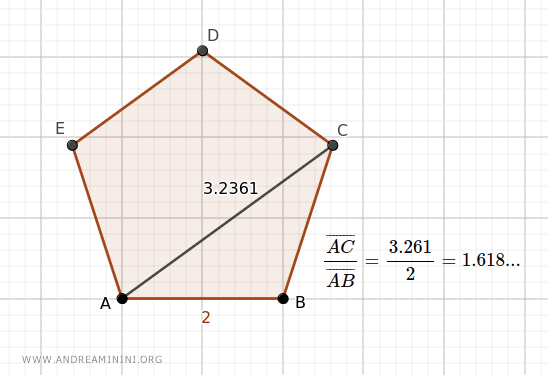
- Il rapporto tra la diagonale e il lato di un pentagono regolare è uguale al numero aureo
Ad esempio, il rapporto tra la diagonale AC del pentagono regolare e il lato AB è uguale a 1.618...
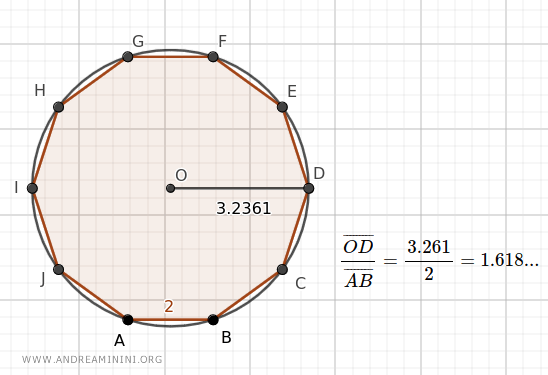
- Il rapporto tra il raggio di una circonferenza e il lato di un decagono regolare inscritto è uguale al numero aureo
Ad esempio, in questo decagono regolare il rapporto tra il raggio della circonferenza (3.2361) e il lato del decagono (2) è uguale al numero aureo.
E così via.
