Forze di attrito
L’attrito è una forza che agisce sempre in opposizione al moto relativo tra due superfici a contatto.
È una resistenza invisibile ma concreta, che si presenta in molte situazioni della vita quotidiana ed è una delle principali forze studiate in fisica.
Perché si verifica?
L’attrito è dovuto a diverse ragioni:
- Le superfici non sono mai perfettamente lisce. Ci sono delle asperità microscopiche che si incastrano tra le superfici, ostacolando il movimento. E' la causa dell'attrito radente.
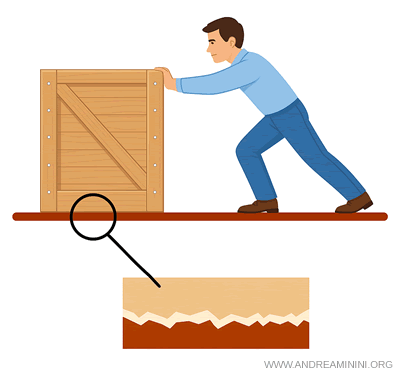
- Alcune forze intermolecolari e legami chimici deboli (van der Waals, interazioni polari, legame a idrogeno) trattengono le molecole tra loro,
- La presenza di fenomeni adesivi in certi materiali è un ulteriore ostacolo al movimento.
Queste diverse cause dell'attrito generano diverse forme di attrito.
Nota. L’attrito trasforma energia meccanica in calore. È una delle principali cause di inefficienza nei sistemi meccanici. Ad esempio, è a causa dell’attrito che i motori si scaldano e le macchine si usurano. Per questa ragione, per ridurre l'attrito tra le parti meccaniche si utilizzano dei lubrificanti.
Tipi di attrito
Esistono diverse forze di attrito, ognuna con caratteristiche specifiche, ma tutte accomunate dalla stessa funzione: rallentare o impedire il movimento.
- Attrito radente
L’attrito radente si manifesta quando due superfici scorrono l’una sull’altra. È il tipo di attrito più noto e si divide in due categorie:- Attrito statico: è la forza che impedisce a un oggetto fermo di iniziare a muoversi. Esiste fino al momento in cui la forza applicata supera una certa soglia.
- Attrito dinamico (o cinetico): entra in gioco quando il corpo ha già iniziato a muoversi e si oppone al suo scorrimento.
Esempio. Spingere un armadio fermo sul pavimento richiede uno sforzo iniziale maggiore per vincere l’attrito statico. Una volta che si muove, mantenerlo in scorrimento richiede meno forza perché subentra l’attrito dinamico.
- Attrito volvente
L’attrito volvente si verifica quando un oggetto rotola su una superficie, come una ruota, una sfera o un rullo. È molto più debole dell’attrito radente, motivo per cui si usano le ruote per trasportare carichi pesanti: riducono la resistenza al movimento.

Esempio. Trascinare una valigia senza rotelle sul marciapiede è faticoso. Se invece la valigia ha delle ruote, ad esempio un trolley, basta uno sforzo minimo per farla rotolare perché entra in gioco l’attrito volvente, che è molto più basso dell'attrito radente.
- Attrito viscoso
L’attrito viscoso si verifica quando un corpo si muove all’interno di un fluido, cioè un gas o un liquido. A differenza dell’attrito radente e volvente, questo tipo di attrito dipende dalla velocità del corpo e dalle caratteristiche del fluido come la viscosità. In particolar modo, nell'aria si parla di attrito viscoso solo se un corpo si sposta a basse velocità.

Esempio. Una pallina che cade in acqua rallenta visibilmente rispetto a una che cade nell’aria. Questo perché l’acqua, essendo più densa, esercita un attrito viscoso maggiore. Per questa ragione è molto più faticoso nuotare. Lo stesso accade nell'aria. Quando una foglia cade dall'albero, il suo moto è rallentato dalla presenza delle molecole presenti nell'aria.
- Attrito aerodinamico (resistenza dell’aria o drag)
Quando un copo si muove a velocità elevate si parla più propriamente di attrito aerodinamico. Qui l’aria non si comporta più solo come fluido viscoso, perché il corpo sposta le molecole d’aria violentemente, creando compressione, turbolenze, riscaldamento e perfino ionizzazione. Questo causa dei fenomeni non lineari, come vortici, onde d’urto e calore. È fondamentale in aerodinamica (auto, aerei, razzi, meteore).
Esempio. La velocità di un aeroplano o di un missile è ridotta dalla presenza delle molecole presenti nell'aria. E' l'attrito viscoso a causare il fenomeno delle stelle cadenti. Quando una piccola roccia spaziale entra nell'atmosfera terrestre, si trasforma in una meteora: l'attrito con le molecole dell'aria la riscalda rapidamente fino a incenerirla, producendo una scia luminosa visibile per pochi secondi nel cielo.
Ecco un riepilogo sintetico delle principali differenze tra le varie forze di attrito che è utile tenere a mente.
| Tipo di attrito | Quando si verifica | Intensità relativa | Dipende da |
|---|---|---|---|
| Attrito statico |
Corpo fermo, impedisce l’inizio del moto | Maggiore dell'attrito dinamico | Natura delle superfici |
| Attrito dinamico |
Corpo in moto, scivolamento | Minore dell’attrito statico | Natura delle superfici |
| Attrito volvente |
Corpo che rotola | Molto minore dell'attrito radente | Geometria del corpo e deformazioni |
| Attrito viscoso |
Corpo in un fluido | Variabile con la velocità | Velocità e viscosità del fluido |
La forza di attrito statico e dinamico
La forza di attrito statico tra un corpo e una superficie è una forza parallela alla superficie di contatto, indicata con $ F_s $.
Il suo verso è opposto a quello che avrebbe il moto del corpo in assenza di attrito (forza applicata $ F_x $), e non dipende dall'area della superficie di contatto.
La condizione di equilibrio statico si esprime come:
$$ \vec{F_s} + \vec{F_x} = 0 $$
Finché la forza applicata al corpo è inferiore alla forza massima di attrito statico, il corpo rimane fermo.
In questa situazione, il modulo delle due forze risulta uguale:
$$ F_x = F_s $$
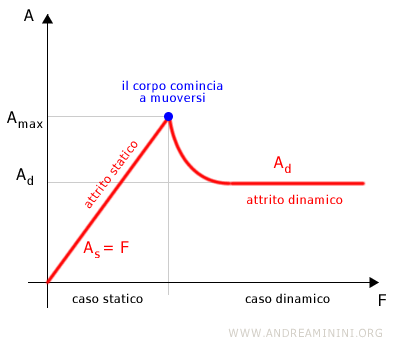
La forza di attrito statico si adatta progressivamente all'intensità della forza applicata, fino a raggiungere un valore massimo, oltre il quale il corpo inizia a muoversi.
La forza massima di attrito statico (detta anche "forza di attrito al distacco") è direttamente proporzionale al modulo della forza premente perpendicolare alla superficie di contatto.
$$ F_{s,max} = \mu_s F_N $$
Dove $ \mu_s $ è il coefficiente di attrito statico che dipende dalle proprietà delle superfici e $ F_N $ è il modulo della forza premente perpendicolare alla superficie di contatto (forza normale).
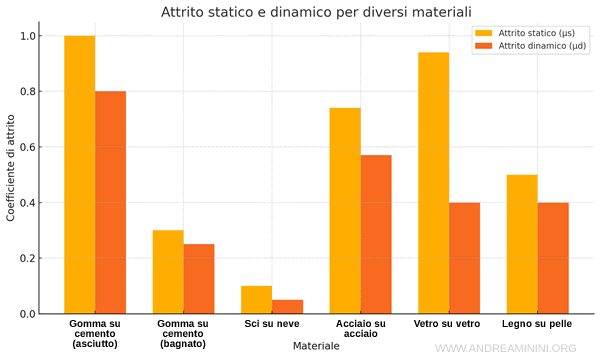
In genere, il coefficiente di attrito statico $ \mu_s $ è compreso tra 0 e 1.2 a seconda dei materiali delle superfici a contatto.
Una volta che il corpo è in movimento, entra in gioco un’altra forza: la forza di attrito dinamico.
Questa forza ha modulo inferiore rispetto all’attrito statico massimo, perché durante il moto gli asperità e le irregolarità delle superfici non riescono più ad agganciarsi efficacemente tra loro.
$$ F_d = \mu_d F_N $$
Per questa ragione il coefficiente di attrito dinamico $ \mu_d < \mu_s $ è minore rispetto a quello statico
Qual è la differenza? L'attrito statico impedisce l'inizio del moto mentre l'attrito dinamico agisce quando il corpo è già in movimento.
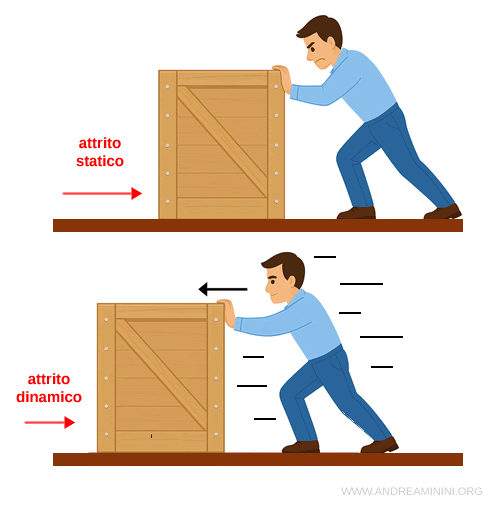
Poiché la forza di attrito statico si adegua alla forza applicata, quando il corpo comincia a muoversi viene raggiunta la forza di attrito massima. Dopodiché entra in gioco l'attrito dinamico.
Un esempio pratico
Una cassa di 100 kg è ferma su un piano inclinato di 20°, qual è la forza di attrito statico?
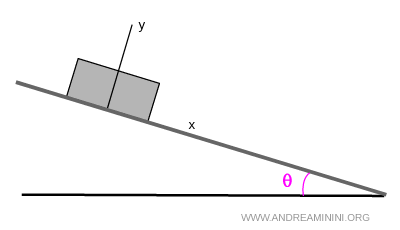
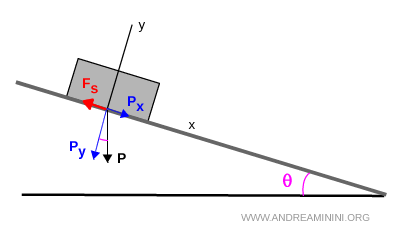
Considero come sistema di riferimento il piano come asse x e la perpendicolare al piano come asse y.
Inizialmente calcolo il modulo della forza peso del corpo.
$$ P = m \cdot g $$
In questo caso la massa del corpo è $ m = 100 \ kg $ mentre l'accelerazione della gravità terrestre è in media $ g = 9,81 \ N/kg $.
$$ P = 100 \ kg \cdot 9,81 \ N/kg $$
$$ P = 100 \ kg \cdot 9,81 \ N/kg $$
$$ P = 981 \ N $$
Il vettore della forza peso P è sempre orientato verso il centro della Terra.
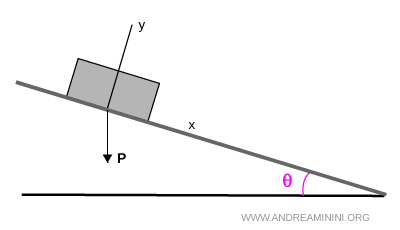
Scompongo la forza peso sugli assi del sistema di riferimento.
$$ \begin{cases}
P_x = P \cdot \sin 20° \\ \\
P_y = P \cdot \cos 20° \end{cases} $$
$$ \begin{cases}
P_x = 981 \ N \cdot 0,34 \\ \\
P_y = 981 \ N \cdot 0,94 \end{cases} $$
$$ \begin{cases}
P_x = 334 \ N \\ \\
P_y = 922 \ N \end{cases} $$
Le componenti della forza peso sugli assi x e y sono Px e Py.
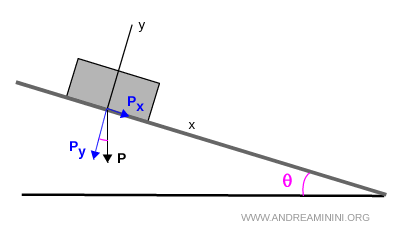
La forza di attrito statico $ F_s $ è la forza parallela al piano che si oppone allo scivolamento della cassa lungo l'asse $x$ e si adegua fino a un massimo $ F_{s,max} $.
Poiché la cassa è ferma, l'equilibrio si ottiene quando $ F_s = P_x $
$$ F_s = P_x = 334 \ N $$
In queste condizioni, la forza di attrito statico che si oppone al moto è $ F_s = 334 \ N $
Se la cassa comincia a muoversi quando il piano è inclinato di 30°, qual è la forza di attrito statico massima?
La formula della forza di attrito statico massimo è la seguente:
$$ F_{s,max} = \mu_s \cdot F_N $$
Ricalcolo la forza normale considerando un'inclinazione del piano di 30°.
$$ \begin{cases}
P_x = P \cdot \sin 30° \\ \\
P_y = P \cdot \cos 30° \end{cases} $$
La forza peso della cassa è sempre la stessa $ P = 981 \ N $
$$ \begin{cases}
P_x = 981 \ N \cdot 0,5 \\ \\
P_y = 981 \ N \cdot 0,87 \end{cases} $$
$$ \begin{cases}
P_x = 491 \ N \\ \\
P_y = 853 \ N \end{cases} $$
La forza normale $ F_N $ è la forza perpendicolare al piano, di reazione vincolare, che si oppone alla forza peso.
$$ F_N = P_y = 853 \ N $$
La forza di attrito statico è, invece, parallela al piano.
$$ F_s = P_x = 491 \ N $$
La forza di attrito statico raggiunge il suo valore massimo proprio quando la cassa inizia a muoversi.
Poiché la cassa comincia a muoversi, questa intensità è anche la forza di attrito statico massimo.
$$ F_{s,max} = 491 \ N $$
Quindi, riprendo la formula dell'attrito statico max e sostituisco i valori che ho appena trovato.
$$ F_{s,max} = \mu_s \cdot F_N $$
$$ 491 \ N = \mu_s \cdot 853 \ N $$
$$ \mu_s = \frac{ 491 \ N }{ 853 \ N} $$
$$ \mu_s = 0,58 $$
Pertanto, in questo esercizio il coefficiente di attrito statico del piano inclinato è 0,58.
E così via.
