La forza di attrito radente
La forza di attrito radente è una forza che si oppone al moto di un corpo a contatto con un piano d'appoggio.
Si tratta di una reazione vincolare che si verifica quando due superfici ruvide slittano l'una sull'altra.
E' causata della forza di coesione tra le superfici a contatto di un corpo e del piano. Dipende dalla rugosità di entrambe le superfici.
La forza di attrito radente è parallela al piano di appoggio e si oppone al moto relativo.
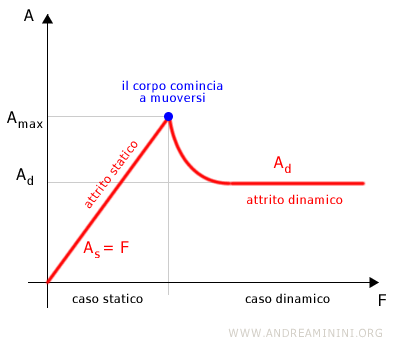
Esistono due tipi di attrito radente.
- L'attrito statico che impedisce a un corpo in condizione di quiete di iniziare a muoversi.
- L'attrito dinamico che ostacola il moto di un corpo già in movimento.
Nota. L'attrito statico è sempre maggiore dell'attrito dinamico perché è più semplice spostare nello stesso verso un corpo già in movimento che un corpo fermo.
Un esempio pratico
A] Caso statico
Considero un corpo poggiato su un piano in stato di quiete (equilibrio statico).
Sul corpo agisce la forza di gravità verso il basso P e la reazione vincolare Rn del piano.
La forza F trascina il corpo verso destra mentre la forza di attrito statico As si oppone al moto.
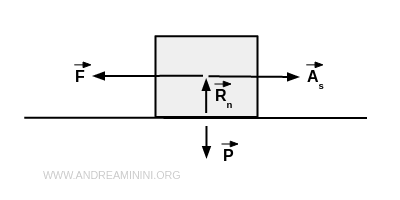
Per il secondo principio della dinamica il corpo è in equilibrio statico quando la somma algebrica delle forze si annulla
$$ \vec{P} + \vec{R_n} + \vec{F} + \vec{A}_s = 0 $$
Proietto tutte le forze coinvolte (vettori) sugli assi x e y rispetto al piano e alla forza trainante
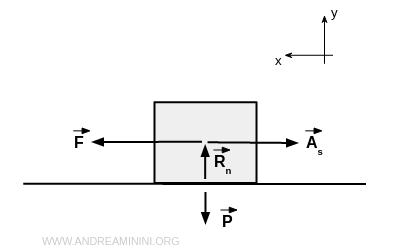
In questo modo trasformo le grandezze vettoriali in un sistema di grandezze numeriche (moduli).
$$ \begin{cases} F - A_s = 0 \ \ \ \ (asse \ x) \\ \\ R_n - P = 0 \ \ \ \ (asse \ y) \end{cases} $$
Ora i valori nel sistema sono i moduli (intensità o lunghezze) dei vettori ossia numeri.
Il segno algebrico dei valori è determinato dal verso dei vettori rispetto agli assi xy che ho scelto.
In genere, per convenzione la forza frenante dell'attrito (As) e la forza di gravità (P) sono negative.
$$ \begin{cases} F - A_s = 0 \ \ \ \ (asse \ x) \\ \\ R_n - P = 0 \ \ \ \ (asse \ y) \end{cases} $$
In questo esempio la direzione dei vettori coincide con il piano di appoggio. Il che semplifica l'analisi.
Nota. Nel problema ci sono due reazioni vincolari (colore blu). Una reazione normale (Rn) che si oppone alla forza di gravità e una reazione tangenziale (parallela) ossia l'attrito che si oppone al moto del corpo. La somma delle due reazioni vincolari è detta reazione totale del vincolo.
Il corpo resta fermo (equilibrio statico) fin quando la forza F è uguale all'attrito statico As ossia F=-As.
$$ \begin{cases} F = A_s \ \ \ \ (asse \ x) \\ \\ R_n = P \ \ \ \ (asse \ y) \end{cases} $$
L'attrito è una reazione vincolare, quindi il suo modulo As si adegua alla forza F che cerca di spostare il corpo.
Tuttavia, l'attrito è limitato a un valore massimo di attrito (Amax)
$$ A_{max} = \mu_s \cdot R_n $$
Dove il coefficiente di attrito statico (μs) è determinato dalla rugosità delle superfici mentre Rn è la reazione normale del piano al peso del corpo.
Pertanto, l'attrito massimo Amax dipende sia dalla rugosità della superficie (μs) e dal peso del corpo da spostare (Rn).
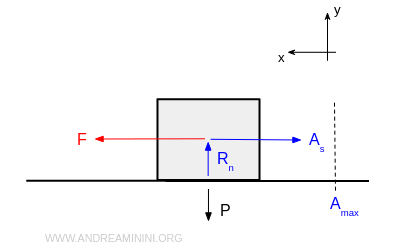
Nota. Se il corpo da spostare è molto pesante, la reazione normale Rn del piano è maggiore. Pertanto, anche il valore dell'attrito massimo è più alto.
Il sistema di equazioni posso riscriverlo sostituendo l'equazione F = As con la disequazione F ≤ Amax
$$ \begin{cases} F \le A_{max} \ \ \ \ (asse \ x) \\ \\ R_n = P \ \ \ \ (asse \ y) \end{cases} $$
Quando la forza tirante F supera l'attrito massimo Amax si verifica una diseguaglianza F > Amax e il corpo comincia a spostarsi nel verso della forza F.
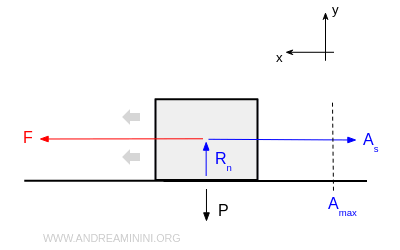
Nel momento in cui il corpo comincia a muoversi si passa dal caso statico al caso dinamico.
B] Caso dinamico
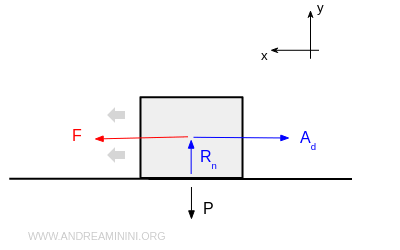
Quando il corpo comincia a muoversi (caso dinamico) l'attrito radente si riduce.
L'attrito di un corpo in movimento è detto attrito radente dinamico (Ad).
L'attrito dinamico è il prodotto tra il coefficiente di attrito dinamico μd e la reazione vincolare Rn (il peso del corpo).
$$ \vec{A_d} = \mu_d \cdot \vec{R_n} $$
L'attrito radente dinamico è costante ed è sempre inferiore all'attrito statico.
Questo accade perché la forza di coesione tra le superfici è minore.
$$ \mu_d < \mu_s $$
Quando il corpo comincia a muoversi cambia anche l'equazione da considerare.
L'equilibrio del moto di un corpo in movimento è F=ma dove le forze sono i vettori P+Rn+F+Ad
$$ \vec{P} + \vec{R_n} + \vec{F} + \vec{A_d} = m \cdot \vec{a} $$
Proietto le forze sugli assi xy rispetto al piano e al verso della forza.
In questo modo ottengo un sistema con grandezze numeriche (moduli).
$$ \begin{cases} F - A_d = m \cdot a_x \\ \\ R_n - P = m \cdot a_y \end{cases} $$
L'attrito dinamico si oppone al moto del corpo in movimento.
Nota. L'attrito statico e l'attrito dinamico si calcolano considerando le caratteristiche delle superfici di entrambi i corpi a contatto. Ad esempio, i coefficienti di attrito del legno sono μs=0.5 e μd=0.3, quelli dell'acciaio sono μs=0.8 e μd=0.4. In ogni caso i coefficienti di attrito sono sempre minori di uno.
Quanto spazio percorre un corpo in movimento
Considero un corpo in movimento su un piano con una velocità v0>0 nell'istante t0.
Questa situazione rientra nel caso dinamico.
$$ \begin{cases} F - A_d = m \cdot a_x \\ \\ R_n - P = m \cdot a_y \end{cases} $$
Il corpo si muove già in movimento senza alcuna forza a spingerlo. Quindi F=0
$$ \begin{cases} - A_d = m \cdot a_x \\ \\ R_n - P = m \cdot a_y \end{cases} $$
Il corpo si muove in orizzontale e la reazione vincolare del piano sorregge il corpo.
Quindi la seconda equazione è uguale a zero.
$$ \begin{cases} - A_d = m \cdot a_x \\ \\ R_n - P - m \cdot a_y = 0 \end{cases} $$
Per trovare la legge oraria del corpo mi concetro sulla prima equazione.
$$ - A_d = m \cdot a_x $$
Da questa equazione ricavo l'accelerazione
$$ a_x = \frac{- A_d}{m} $$
Sapendo che l'attrito dinamico è Ad=μdRn.
$$ a_x = \frac{- \mu_d \cdot \vec{R_n}}{m} $$
La reazione vincolare normale Rn (verticale) è uguale al peso (P) del corpo per la forza gravità (g) ossia Rn=P=mg
$$ a_x = \frac{- \mu_d \cdot \vec{m \cdot g}}{m} $$
$$ a_x = - \mu_d \cdot g $$
Quest'ultima è la legge dell'accelerazione.
Sapendo che l'accelerazione è la derivata prima della velocità rispetto al tempo.
$$ v_x = \int a_x \ dt $$
$$ v_x = \int - \mu_d \cdot g \ dt $$
L'integrale di ∫-μd·g dt rispetto al tempo è -μd·g·t + c
$$ v_x = - \mu_d \cdot g \cdot t + c $$
Dove la costante c è la velocità iniziale v0 al tempo t0.
$$ v_x = - \mu_d \cdot g \cdot t + v_0 $$
Una volta nota la legge della velocità, posso ricavare la legge oraria.
Sapendo che la velocità è la derivata della legge oraria rispetto al tempo
$$ s_x = \int v_x \ dt $$
$$ s_x = \int - \mu_d \cdot g \cdot t + v_0 \ dt $$
$$ s_x = \int - \mu_d \cdot g \cdot t \ dt + \int v_0 \ dt $$
$$ s_x = - \mu_d \cdot g \cdot t \cdot \frac{t}{2} + v_0 \cdot t + c $$
$$ s_x = \frac{- \mu_d \cdot g \cdot t^2}{2} + v_0 \cdot t + c $$
Dove la costante c=s0 è il punto dello spazio in cui si trova il corpo nell'istante t0.
$$ s_x = \frac{- \mu_d \cdot g \cdot t^2}{2} + v_0 \cdot t + s_0 $$
Per semplicità considero s0=0
$$ s_x = v_0 \cdot t - \frac{\mu_d \cdot g \cdot t^2}{2} $$
Quest'ultima è la legge oraria del corpo in movimento.
Il corpo in movimento si ferma quando la velocità si annulla.
$$ v_x = 0 $$
$$ - \mu_d \cdot g \cdot t + v_0 = 0 $$
Da quest'ultima equazione ricavo l'istante di tempo t* in cui il corpo si ferma
$$ t* = \frac{ v_0 }{ \mu_d \cdot g } $$
Una volta trovato l'istante di tempo t* in cui il corpo si ferma, lo sostituisco nella legge oraria.
$$ s_x = v_0 \cdot (t*) - \frac{\mu_d \cdot g \cdot (t*)^2}{2} $$
$$ s_x = v_0 \cdot ( \frac{ v_0 }{ \mu_d \cdot g } ) - \frac{\mu_d \cdot g \cdot ( \frac{ v_0 }{ \mu_d \cdot g } )^2}{2} $$
$$ s_x = \frac{ v_0^2 }{ \mu_d \cdot g } - \frac{\mu_d \cdot g \cdot ( \frac{ v_0 }{ \mu_d \cdot g } )^2}{2} $$
$$ s_x = \frac{ v_0^2 }{ \mu_d \cdot g } - \frac{1}{2} \cdot \mu_d \cdot g \cdot \frac{ v_0^2 }{ (\mu_d \cdot g)^2 } $$
$$ s_x = \frac{ v_0^2 }{ \mu_d \cdot g } - \frac{1}{2} \cdot \frac{ v_0^2 }{ \mu_d \cdot g } $$
$$ s_x = \frac{ v_0^2 }{ \mu_d \cdot g } \cdot ( 1 - \frac{1}{2} ) $$
$$ s_x = \frac{ v_0^2 }{ \mu_d \cdot g } \cdot \frac{1}{2} $$
Quest'ultima formula mi permette di calcolare il punto sx in cui il corpo si ferma.
L'attrito statico
L'attrito statico impedisce a un corpo in condizione di quiete di iniziare a muoversi.
Considero un corpo appoggiato su un piano orizzontale.
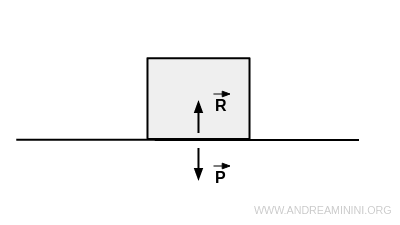
In equilibrio statico la reazione vincolare R compensa esattamente la forza peso P del corpo.
$$ \vec{R} + \vec{P} = 0 $$
Applico al corpo una forza F diagonale per trascinarlo.
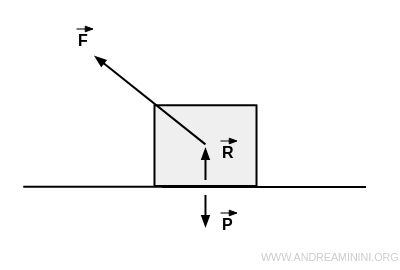
In questo caso la forza F è composta da due componenti ortogonali
- una componente normale alla reazione vincolare del piano (Fv) verso l'alto
- una componente parallela al piano (Fo) verso sinistra
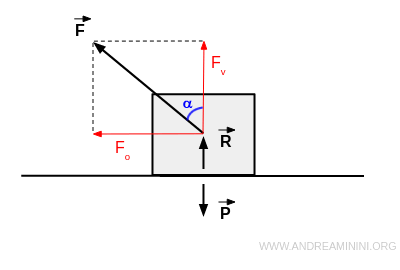
La forza applicata forma un angolo rispetto alla retta normale al piano.
Usando l'angolo posso esprimere le due forze usando le funzioni trigonometriche del seno e coseno
$$ \vec{F_v} = F \cdot \cos \alpha $$
$$ \vec{F_o} = F \cdot \sin \alpha $$
Quindi posso esprimere le stesse componenti Fv e Fo anche usando il modulo della forza applicata F
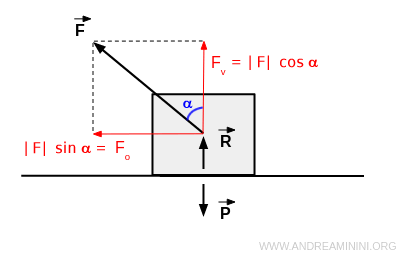
In equilibrio statico (corpo fermo) la reazione vincolare del piano compensa la forza peso P al netto della forza
$$ \vec{R} + \vec{P} + \vec{F} = 0 $$
La reazione vincolare R posso scomporla in due componenti ortogonali.
- La forza di attrito radente (Fa) si oppone al moto orizzontale e dipende dalle caratteristiche del piano.
- La reazione normale (N) si oppone al moto verticale. E' il piano che sostiene il corpo opponendosi alla forza di gravità.
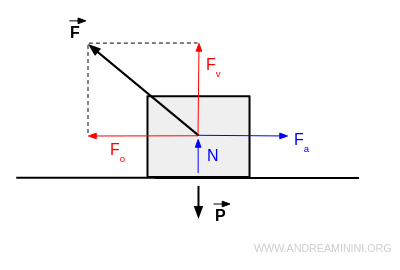
Scompongo l'equazione vettoriale R+P+F=0 in due direzioni ortogonali: parallela e normale (verticale) al piano
$$ \begin{cases} F_a + F_o = 0 \\ \\ N-P+F_v = 0 \end{cases} $$
Sull'asse parallelo (orizzontale) al piano agisce verso sinistra la componente Fo della forza applicata e verso destra la forza di attrito radente Fa della reazione vincolare.
Sull'asse normale (verticale) al piano agisce verso l'alto il modulo N della reazione vincolare e la componente Fv, il modulo P della forza peso, invece, agisce verso il basso.
Nota. Nelle due equazioni del sistema sono presenti le componenti dei vettori sugli assi ortogonali. Quindi, si tratta di grandezze scalari. Non sono vettori.
Esplicito la forza di attrito radente e la reazione normale vincolare
$$ \begin{cases} F_a = - F_o \\ \\ N = P-F_v \end{cases} $$
La seconda equazione N=P-Fv è la condizione di appoggio.
Il corpo comincia a muoversi solo quando il modulo della forza orizzontale Fo supera la forza di attrito.
$$ F_o > F_a $$
La forza di attrito Fa =μs|N| è il prodotto tra il coefficiente di attrito statico μs e il modulo della forza normale |N|.
Quindi, l'attrito dipende dalle caratteristiche del piano e dal peso del corpo.
$$ F_o > \mu_s \cdot N $$
Sapendo che Fo=F sin α
$$ F \cdot \sin \alpha > \mu_s \cdot N $$
Devo però considerare anche il caso in cui la forza applicata sia eccessiva e sollevi il corpo anziché trascinarlo.
Per evitare questo devo anche applicare la condizione P≥Fv.
$$ P \ge F_v $$
Il modulo della forza peso deve essere maggiore o uguale alla forza di sollevamento Fv.
Sapendo che Fv=F cos α
$$ P \ge F \cdot \cos \alpha $$
Quest'ultima condizione indica che la forza applicata F non solleva il corpo.
Pertanto, il corpo si muove soltanto per trascinamento sul piano.
L'attrito radente dinamico
L'attrito radente dinamico è una forza che si oppone al moto di un corpo quando è già in movimento. $$ \vec{F_a} = \mu_d \cdot N \cdot ( -\vec{u_v} ) $$ Dove μd è il coefficiente di attrito dinamico, N è il modulo della forza normale del piano che spinge il corpo verso l'alto e uv è il versore della velocità.
Il coefficiente di attrito dinamico μd è sempre inferiore al coefficiente di attrito statico μs perché occorre una forza maggiore per iniziare un moto piuttosto che mantenerlo.
$$ \mu_d < \mu_s $$
Il verso dell'attrito dinamico è contrario a quello della velocità del corpo (-uv) perché si oppone al moto del corpo.
Il coefficiente di attrito radente dinamico dipende dal materiale di cui sono composte le superfici a contatto del piano e del corpo.
Esempio. Se il piano è acciaio è μd=0.4, se è acciaio lubrificato scende a μd=0.05, se il piano è di gomma è μd=0.8, ecc.
Oltre alle superfici, l'attrito radente dipende anche dalla pressione esercitata dal corpo sul piano (N).
Quanto più è alta la pressione del corpo sul piano, tanto maggiore è la forza frenante dell'attrito dinamico.
In generale l'equazione del moto di un corpo è
$$ \vec{F} = m \cdot \vec{a} $$
Dove m è la massa e il vettore a è l'accelerazione.
Considerando l'azione dell'attrito radente dinamico l'equazione diventa
$$ \vec{F} + F_a = m \cdot \vec{a} $$
Sapendo che l'attrito dinamico è una forza opposta Fa=-μdNuv
$$ \vec{F} - \mu_d N \vec{u_v} = m \cdot \vec{a} $$
Nota. Quando la forza F è uguale e contraria alla forza di attrito radente Fa il corpo si muove in moto uniforme. In questo caso l'accelerazione è nulla e il corpo continua a muoversi in equilibrio dinamico.
E così via.
