Il metodo della proiezione delle forze sugli assi cartesiani

Quando si studiano le forze che agiscono su un corpo in equilibrio, è fondamentale proiettare tutti i vettori delle forze sugli assi di riferimento (di solito $x$ e $y$) per poter applicare correttamente le condizioni di equilibrio.

Questo metodo è detto "metodo della proiezione" o "metodo della scomposizione vettoriale".

A volte è indicato anche come "metodo delle componenti".

Nota. Questa tecnica non ha un "nome ufficiale" nei libri di fisica scolastici. Ad esempio, i manuali di fisica generale o fisica 1 (tipo Halliday, Mazzoldi-Nigro-Voci, Serway) non danno un nome univoco, ma parlano di "scomposizione vettoriale", "proiezione delle forze sugli assi cartesiani", "componenti cartesiane delle forze". E' un peccato perché è molto utile per iniziare a studiare i problemi di equilibrio e andrebbe imparato a usarlo fin da subito nei corsi di fisica.

Quali sono le condizioni di equilibrio (statica)

Per un corpo in equilibrio traslazionale (cioè che non si muove né accelera), devono essere soddisfatte queste due equazioni:

• $\sum F_x = 0 \quad \text{(somma delle forze lungo l'asse x)} $
• $\sum F_y = 0 \quad \text{(somma delle forze lungo l'asse y)} $

Perché si proiettano le forze?

I vettori forza possono avere direzioni qualsiasi: inclinata, verticale, orizzontale…

Per poterli sommarli algebricamente, devo scomporli lungo gli assi cartesiani, cioè trovare le componenti $F_x$ e $F_y$ di ogni forza.

Ad esempio, una forza $F$ inclinata di un angolo $\theta$ rispetto all’orizzontale avrà due componenti:

• la componente orizzontale è $F_x = F \cos\theta$
• la componente verticale è $F_y = F \sin\theta$

Poi cosa si fa? Dopo aver scomposto tutte le forze in componenti lungo $x$ e $y$, si impone la condizione di equilibrio $ R_x=0 $ e $ R_y= 0 $: 

• si sommano tutte le componenti lungo $ x $ e si impone $ R_x = \sum F_x = 0 $
• si sommano tutte le componenti lungo $ y $ e si impone $ R_y = \sum F_y = 0 $

Se serve, si applica anche la condizione di equilibrio rotazionale:

• $\sum M_O = 0 \quad \text{(somma dei momenti rispetto a un punto O)}$

Queste condizioni sono semplicemente la traduzione matematica di “non si muove”.

Quindi, per risolvere i problemi di equilibrio, dopo aver individuato i vincoli e le relative reazioni, è necessario scegliere un sistema di riferimento cartesiano, preferibilmente quello che semplifica i calcoli.

A questo punto si proiettano tutte le forze sugli assi $x$ e $y$, si applicano le condizioni di equilibrio traslazionale $\sum F_x = 0$ e $\sum F_y = 0$, e si sfruttano i momenti in modo strategico per determinare le incognite.

Un esempio pratico

Un blocco è appoggiato su un piano inclinato di 30° rispetto all’orizzontale.

La massa del blocco è $m = 10\, \text{kg}$. Il blocco è fermo.

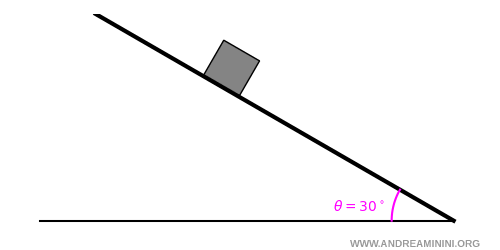
Devo calcolare la forza normale e l’intensità della forza di attrito statico che impedisce al blocco di scivolare.

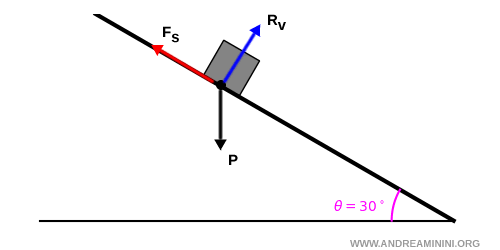
Per prima cosa individuo le forze agenti e le reazioni vincolari:

• Peso: $\vec{P} = m \vec{g}$
• Forza normale $\vec{R_V}$ (reazione vincolare)
• Forza di attrito statico $\vec{F_S}$

Le aggiungo nello schizzo grafico del piano inclinato per analizzarle.

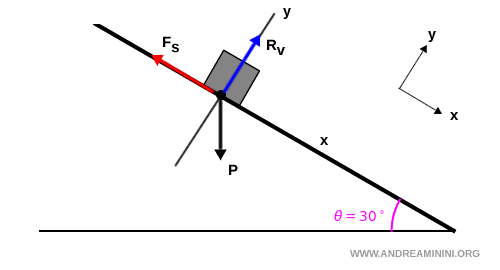
Poi scelgo il sistema di riferimento.

In questo caso, il sistema cartesiano che semplifica i calcoli è quello che ha l'asse x lungo il piano inclinato e l'asse y perpendicolare al piano.

• Asse $x$: lungo il piano inclinato
• Asse $y$: perpendicolare al piano

In questo modo due forze su tre sono già allineate lungo gli assi cartesiani.

Il vettore della forza peso non si trova lungo un asse cartesiano, quindi devo scomporlo usando il metodo della proiezione.

Proietto il vettore $ \vec{P} $ lungo gli assi.

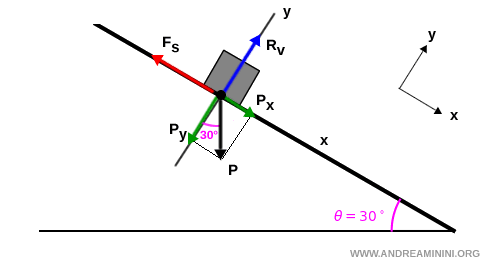
L'angolo tra il vettore $ \vec{P} $ e l'asse y è congruente con $ \theta = 30° $.

Questo mi permette di calcolare le componenti del vettore $ \vec{P} $ sui due assi.

$$ P_x = mg \sin\theta = 10 \ Kg \cdot 9.8 \ N/Kg \cdot \sin(30°) = 49\, \text{N} $$

$$ P_y = mg \cos\theta = 10 \ Kg \cdot 9.8 \ N/Kg \cdot \cos(30°) \approx 84.9\, \text{N} $$

A questo punto applico le condizioni di equilibrio su entrambi gli assi di riferimento:

$$ \begin{cases} \sum F_x = 0 \\ \\ \sum F_y = 0 \end{cases} $$

$$ \begin{cases} P_x - F_s = 0 \\ \\ F_N - P_y = 0 \end{cases} $$

Nota. La forza di attrito statico $ F_s $ ha il segno meno perché ha il verso opposto al semiasse x positivo del sistema di riferimento che ho scelto. Per la stessa ragione la forza peso $ P_y $ ha il segno meno, in quanto ha il verso opposto al semiasse y del sistema di riferimento.

Sostituisco le componenti $ P_x $ e $ P_y $ della forza peso e svolgo i calcoli.

$$ \begin{cases} 49\, \text{N} - F_S = 0 \\ \\ R_V - 84.9\, \text{N} = 0 \end{cases} $$

$$ \begin{cases} F_S = 49\, \text{N}  \\ \\ R_V = 84.9\, \text{N}  \end{cases} $$

Quindi, il modulo della reazione normale è $ R_V = 84.9 \ N $ mentre la forza di attrito statica è $ F_S = 49 \ N $.

E così via.