Forza normale
La forza normale è la forza esercitata da una superficie per sostenere un oggetto e impedire che lo attraversi. È sempre perpendicolare alla superficie stessa.
Quando un oggetto è a contatto con una superficie, questa esercita una forza di reazione perpendicolare al piano di appoggio.
Questa forza si chiama forza normale.
Nota. La forza normale non va confusa con la forza peso, che è sempre diretta verso il basso, verso il centro della Terra. Le due forze possono coincidere, ma non è sempre così.
Si chiama "normale" perché è perpendicolare alla superficie di contatto: in geometria, una retta perpendicolare a un piano si dice appunto "normale" al piano.
Quindi, la forza normale è la reazione della superficie nella direzione normale (cioè ortogonale) rispetto al punto di contatto.
La forza normale su una superficie orizzontale
Se l’oggetto è appoggiato su una superficie perfettamente orizzontale e non ci sono altre forze verticali, la forza normale equilibra esattamente la forza peso.
Esempio
Considero una scatola con una massa di 10 kg sul pavimento.
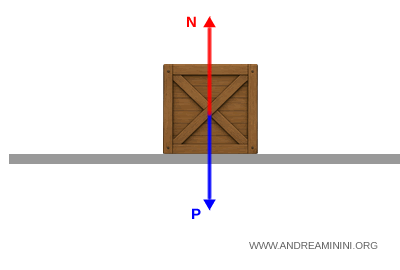
Le forze applicate a una scatola su un pavimento sono:
- Peso: diretto verso il basso $$ P = mg $$
- Forza normale: diretta verso l’alto $$ N = mg $$
La scatola resta ferma se le due forze si annullano $ P+N = 0 $.
La forza peso della scatola va verso il centro della terra ed è circa 98 N.
$$ P = mg = 10 \cdot 9.8 = 98 \, \text{N} $$
Per sorreggere la scatola il pavimento contrappone una forza normale identica ma in verso opposto.
$$ N = 98 \text{N} $$
In questo caso il modulo della forza normale è uguale a quello della forza peso.
La forza normale su piano inclinato
Quando l’oggetto è su un piano inclinato, la situazione cambia.
In questo caso la forza normale è minore del peso, perché la forza peso è sempre verticale mentre la forza normale è perpendicolare alla superficie inclinata.
Ora la componente normale del peso è:
$$ N = mg \cdot \cos(\theta) $$
Dove $ \theta $ è l’angolo d’inclinazione del piano.
Esempio
Considero una scatola con una massa di 10 kg su rampa inclinata di 30°
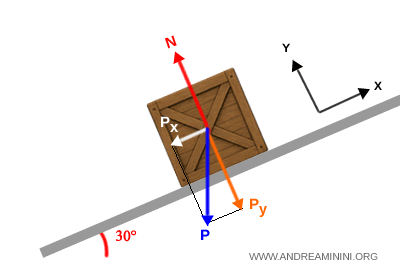
La forza peso che va verso il centro della terra è
$$ P = mg = 10 \cdot 9.8 = 98 \, \text{N} $$
La forza normale perpendicolare al piano inclinato è.
$$ N = 98 \cdot \cos(30^\circ) \approx 84.9 \, \text{N} $$
Quindi la forza normale è più piccola della forza peso.
La forza normale con altre forze applicate
Quando sull’oggetto agisce una forza aggiuntiva verso il basso (es. la mano che lo spinge), allora la forza normale diventa maggiore della forza peso.
Esempio
Considero una scatola con una massa di 10 kg su un piano orizzontale.
La forza peso della scatola è
$$ P = mg = 10 \cdot 9.8 = 98 \, \text{N} $$
Poi spingo una scatola verso il basso con una forza di 20 N.
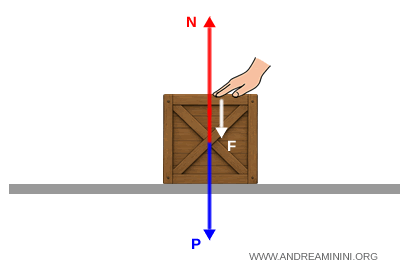
In questo caso la forza normale deve bilanciare sia il peso che la forza aggiuntiva. Quindi, è superiore alla forza peso.
$$ N = P + F = 98 + 20 = 118 \, \text{N}$$
Questi esempi dimostrano che la forza normale è sempre perpendicolare alla superficie di contatto ma non coincide sempre con la forza peso.
Il risultato finale dipende dall’inclinazione del piano e dalle forze aggiuntive.
E così via.
