Forze ed equilibrio in un sistema con corda e carrucola
Quando un corpo è appeso a una corda, il sistema si trova in equilibrio grazie a un gioco di forze che si bilanciano perfettamente.
La tensione di una corda tirata
Se una corda sottile è tirata da due estremità con forze opposte e uguali, in tutta la sua lunghezza si crea una tensione costante $ T $.
Questo vale se la massa della corda è trascurabile.
Esempio
Considero una fune tesa tra due pali.
Se tiro la fune con una forza di $ F_1 = 50 \ N $ da una parte e qualcun altro fa lo stesso dall’altra parte $ F_2 = 50 \ N $, in ogni punto della fune c’è una tensione $ T = 50 \ N $.
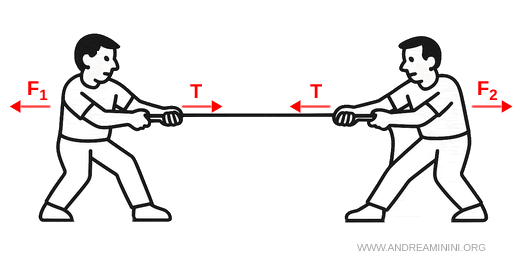
Lo stesso accade se taglio la corda in un punto qualsiasi e poi cerco di tenerle unite, la tensione $ T $ rappresenta la forza che le due parti della corda esercitano per rimanere unite.
Ogni parte eserciterebbe una forza di 50 N per contrastare quella dell’altra.
Corpo appeso a una corda
Quando una corda sostiene un corpo di peso $ P $, la tensione nella corda è esattamente uguale al peso:
$ T = P $
Anche il punto di fissaggio (soffitto o parete) subisce una forza pari a $ T $, ma diretta verso il basso.
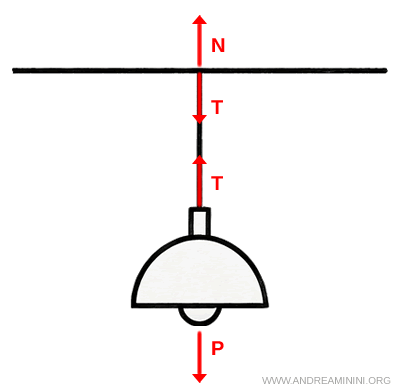
Questa è bilanciata da una reazione vincolare $ N $ al soffitto che mantiene il sistema in equilibrio.
Esempio
Se un lampadario pesa 5 kg (circa 49 N), la corda è tesa con $ T = 49 \ N $.
Il soffitto “reagisce” con una forza uguale e contraria $ N = 49 \ N $.
Uso della carrucola
Una carrucola ideale (senza massa e senza attriti) serve a cambiare la direzione della tensione, non la sua intensità.
Esempio
Se sollevo un peso di 5 kg con una corda passante su una carrucola, la tensione nella corda rimane sempre $ T = P $, anche se la tiro in orizzontale o verso il basso.
Sul peso agiscono due forze: il suo peso $ P $ (verso il basso) e la tensione della corda $ T = P $ (verso l’alto).
Per semplicità considero una carrucola ideale, cioè priva di massa
Se tiro la corda per sollevarlo, devo applicare una forza $ F $ verso il basso pari a $ T = P $.
Quindi, per sollevare un peso di 5 kg (circa 49 N), devo tirare la corda con una forza di 49 N.
Qual è l'equilibrio delle forze sulla carrucola?
La carrucola è, invece, sottoposta a tre forze.
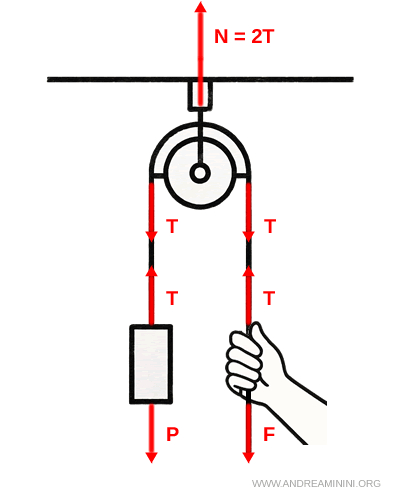
- Una forza $ N $ verso l’alto dal cavo che la sostiene.
- Due forze $ T $ verso il basso: una proveniente dalla fune collegata al peso, l’altra dalla fune che sto tirando.
Questo significa che per mantenere l’equilibrio è necessaria una reazione vincolare doppia sulla carricola:
$ \vec{N} + \vec{T} + \vec{T} = 0 $
Quindi, se l'oggetto pesa 49 N, la staffa che sostiene la carrucola deve esercitare una forza verso l’alto di $ N = 98 \ N $.
$$ \vec{N} = - 2 \vec{T} $$
Pertanto, la reazione vincolare $ N $ sulla staffa è doppia rispetto al peso $ P $ che devo sollevare.
Nota. In tutti questi casi, ho considerato la corda ideale, cioè perfettamente flessibile e senza massa, la tensione rimane costante lungo tutta la sua lunghezza, a meno che il problema non specifichi diversamente.
Un esempio pratico
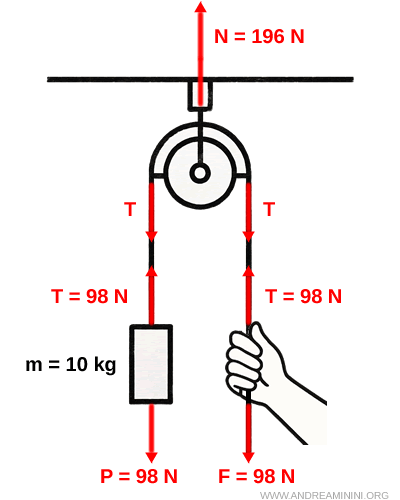
Un blocco di massa $m = 10 \ kg $ è appeso a una corda che passa su una carrucola ideale.
All’altro capo della corda c’è una persona che tira verso il basso con una forza costante per mantenere il blocco in equilibrio statico (cioè fermo).
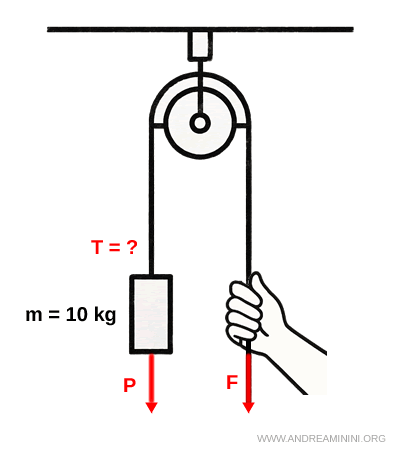
La carrucola è fissata a un soffitto tramite una staffa.
Qual è la tensione nella corda? Qual è la forza che l’omino deve applicare? Qual è la forza che la staffa deve esercitare sulla carrucola per mantenerla in equilibrio?
Per prima cosa calcolo la forza peso dell'oggetto con massa $ m = 10 \ kg $ sapendo che l'accelerazione della gravità terrestre è in media $ g = 9.8 \ N /kg $$.
$$ P = m \cdot g = 10 \ kg \cdot 9.8 \ N / kg = 98 \ N $$
La tensione sulla corda $T$ deve equilibrare il peso del blocco:
$$ T = P = 98 \ N $$
Siccome la carrucola è ideale e la corda è ideale, la tensione è la stessa ovunque:
Quindi, la forza che deve applicare la persona sull’altro capo della corda.
$$ F = T = 98 \ N $$
Sulla carrucola agiscono tre forze: la forza normale $N$ verso l’alto (reazione della staffa) e due tensioni $T$, entrambe verso il basso (una dal lato del blocco e una dal lato che tira la persona)
Quindi, l'equilibrio verticale delle forze è
$$ N = 2 \cdot T = 2 \cdot 98 \ N = 196 \ N $$
Come previsto, la reazione vincolare sulla staffa è doppia rispetto al peso dell'oggetto.
E così via.
