La forza (fisica)
Cos'è la forza
La forza (F) è una grandezza che esprime l’interazione tra i corpi. Misura la variazione di uno stato di quiete o di moto di un punto materiale.
Per modificare lo stato di quiete o di moto di un corpo devo esercitare una certa azione.
La forza misura l'azione.
L'unità di misura della forza è il kg m s-2 anche detta newton (N)
$$ N = kg \ m^{-2} $$
Un newton (1 N) causa un'accelerazione di m s-2 a un corpo con una massa di 1 kg
Nota. La forza non è solo la causa del passaggio dallo stato di quiete al moto, ma anche l'inverso (dal moto allo stato di quiete) o della variazione del moto. Ad esempio, quando un giocatore colpisce la palla di testa, stoppa o blocca un passaggio (azione) la palla varia il suo moto a causa di una forza esterna.

Per la seconda legge di Newton la forza è uguale alla massa (m) per l'accelerazione (a).
$$ \vec{F} = m \cdot \vec{a} $$
La massa (m) è anche detta massa inerziale perché la massa esprime l'inerzia del corpo, ossia la sua resistenza a modificare il proprio moto o stato di quiete.
Nota. In genere si parla di punto materiale anziché di corpo per intendere un corpo dotato di massa ma privo di struttura. La forma di un corpo influisce sul moto. In questo modo si semplifica lo studio della dinamica.
La forza è una grandezza vettoriale perché è determinata dal prodotto tra uno scalare (massa) per un vettore (l'accelerazione).
Pertanto, la forza ha un'intensità, una direzione e un verso.
Esempio. A parità di intensità (modulo) l'effetto di una forza cambia con la direzione e il verso. Ad esempio, nel primo caso la forza sposta un oggetto verso destra, nel secondo caso verso sinistra, nel terzo caso deforma l'oggetto verso il basso senza produrre alcun moto.
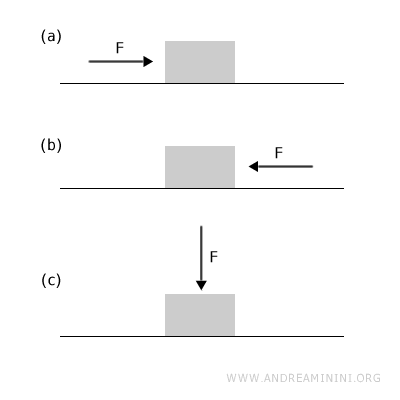
Un esempio pratico
Esempio 1
Una palla è ferma sul pavimento.
Ciò non vuol dire però che non ci siano delle forze sulla palla.
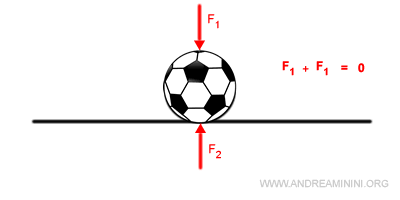
Sulla palla interagiscono due forze opposte che si compensano tra loro.
- La forza gravitazionale spinge la palla verso il basso (F1).
- Il pavimento esprime una forza di reazione vincolare verso l'alto (F2).
La palla è ferma perché le due forze si compensano.
Nota. Se la forza di reazione vincolare F2 fosse inferiore alla forza F1=m·a il piano si romperebbe. Ad esempio, è il caso di una palla di acciaio posta su una scatola di cartone. Il piano della scatola si piegherebbe fino a rompersi.
E' un esempio pratico di interazione tra forze in un oggetto privo di moto.
Esempio 2
Se lanciassi la palla nel vuoto dello spazio., non essendoci alcun attrito, la palla continuerebbe a muoversi nello spazio senza mai fermarsi.

Durante il moto rettilineo uniforme la palla non è soggetta ad alcuna forza anche se si muove.
La variazione del moto della palla si verifica soltanto quando incontra un'altra forza (es. forza gravitazionale di un pianeta oppure un urto con un altro oggetto).
Nota. Nell'antichità si pensava che la forza fosse la causa del movimento. Questo è errato perché, come dimostra l'esempio, il movimento di un corpo potrebbe verificarsi anche in assenza di forze agenti. Inoltre, come dimostra il precedente esempio, un oggetto fermo potrebbe essere sottoposto a forze. Pertanto, la forza non è la causa del moto bensì la forza è la causa della variazione del moto o della variazione dello stato di quiete. E' la prima legge di Newton (o principio di inerzia).
Come si misura la forza
La forza viene misurata tramite uno strumento detto dinamometro.
Il dinamometro è sostanzialmente una molla tarata che inizialmente è scarica.
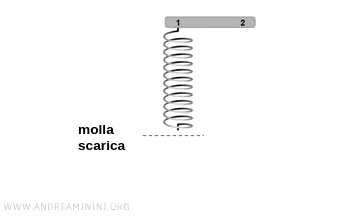
Quando appendo un oggetto di massa m all'estremità inferiore della molla, questa si estende verso il basso per effetto della forza di gravità (g).
La molla "caricata" del peso si estende fino a raggiungere una nuova posizione di equilibrio.
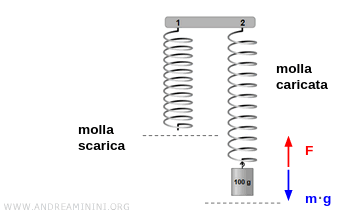
Nella nuova posizione di equilibrio la molla compensa la forza di gravità (g) nei confronti della massa (m).
Pertanto, la forza (F) è proporzionale all'allungamento della molla.
$$ \vec{F} = m \cdot \vec{v} $$
In assenza di altre forze, il dinamometro sta misurando la forza di gravità terrestre.
La dimostrazione matematica della formula F=ma
Secondo la seconda legge della dinamica la forza è il prodotto tra la massa del corpo e l'accelerazione.
$$ \vec{F} = m \cdot \vec{a} $$
Quanto più alta è la massa (m) del corpo, tanto maggiore è la forza (F) necessaria per accelerare un punto materiale.
Sapendo che la forza (F) è la variazione del moto di un corpo di massa m.
$$ \vec{F} = \frac{d(m \vec{v})}{dt} $$
Dove v è il vettore velocità.
Applico la regola della derivata del prodotto.
$$ \vec{F} = m'\vec{v} + m \vec{v}' $$
Sulla Terra la massa di qualsiasi corpo è considerata costante.
Sapendo che la derivata di una costante è zero.
$$ \vec{F} = 0 \cdot \vec{v} + m \vec{v}' $$
Nota. In realtà la massa non è costante. Con Einstein si è capito che anche la massa è relativa. La massa di un corpo aumenta con la velocità e la forza di gravità. Tuttavia, le variazioni della massa significative si verificano soltanto a velocità prossime alla luce.
La derivata prima della velocità v' è, invece, l'accelerazione (a)
Anche l'accelerazione è un vettore.
$$ \vec{F} = 0 \cdot \vec{v} + m \cdot \vec{a} $$
Elimino il primo termine in quanto è un prodotto per zero.
$$ \vec{F} = m \cdot \vec{a} $$
In questo modo ottengo la formula della seconda legge di Newton.
L'analisi dimensionale della forza
La formula della forza è
$$ \vec{F} = m \cdot \vec{a} $$
L'analisi dimensionale della formula è
$$ \vec{F} = [M] \cdot \frac{[L]}{[T]^{2}} = [M] \cdot [L] \cdot [T]^{-2} $$
Dove la massa è M, l'accelerazione è una lunghezza L fratto il tempo T alla seconda
L'unità di misura della massa è il chilogrammo (kg), l'unità di misura della lunghezza è il metro (m), l'unità di misura del tempo è il secondo (s).
$$ \vec{F} = m \cdot \frac{kg}{s^{2}} = m \cdot kg \cdot s^{-2}$$
Pertanto, l'unità di misura della forza è il kg m s-2
E' detta anche newton (N)
$$ 1 \ N = kg \ m \ s^{-2} $$
Un newton (1 N) provoca un'accelerazione di ms-2 di un punto massa pari a 1 kg
E così via.
