La forza elastica

La forza elastica è una forza che ha origine dalla deformazione dei corpi.

Per spiegare la forza elastica in fisica, in genere si utilizza l'esempio di una molla priva di massa.

Tuttavia, qualsiasi corpo è dotato di elasticità.

Ad esempio, un corpo solido sottoposto a compressione deforma temporaneamente la propria struttura chimica. Quando la compressione cessa, il solido torna alla propria situazione iniziale. Anche questa è una forza elastica.

A riposo la molla a una lunghezza pari a l₀.

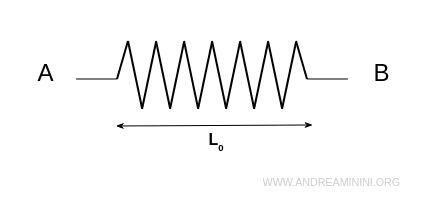
Quando tiro la molla a entrambe le estremità A e B, la molla si allunga fino a L.

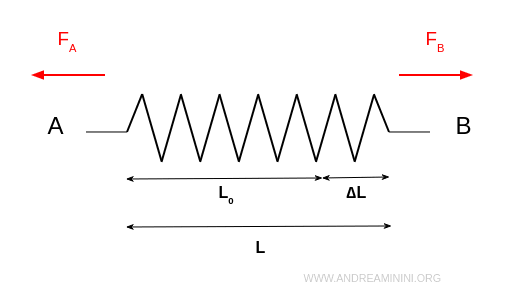
La lunghezza della molla estesa è pari alla lunghezza a riposo (L₀) più l'allungamento (ΔL).

$$ L = L_0 + \Delta L $$

Quando la molla è estesa si sviluppano due forze elastiche uguale e opposte F₁, F₂ in entrambi i capi della molla che cercano di riportarla alla condizione iniziale.

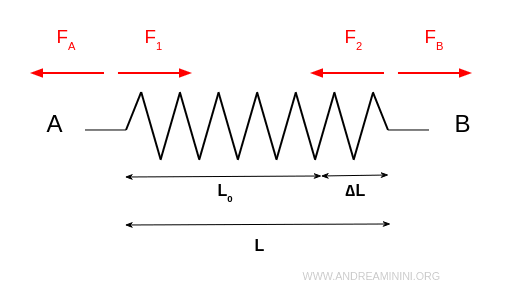
Secondo la legge di Hooke le forze elastiche sono proporzionali all'allungamento.

$$ F_E = k \cdot \Delta L $$

Dove k è la costante elastica della molla (o coefficiente di elasticità).

Analisi dimensionale. Sapendo che la forza elastica F_E è una forza, si misura in N. $$ F_E = k \cdot \Delta L $$ $$ [F] = k \cdot \Delta L $$ L'allungamento ΔL è invece una lunghezza e si misura in metri. $$ [F] = k \cdot \Delta [L] $$ Di conseguenza, il coefficiente di elasticità k deve essere una grandezza [F][L]^-1 e si misura in N/m (Newton fratto metri).

La legge oraria del movimento di una molla si basa sul moto oscillatorio armonico ed è la seguente:

$$ x(t) = A \sin ( \omega t + \phi ) $$

Dove ω sono le pulsazioni e φ è la fase.

La velocità è la derivata prima della legge oraria

$$ v(t) = \omega \cdot A \cos(\omega t + \phi) $$

L'accelerazione è la derivata seconda della legge oraria

$$ a(t) = - \omega^2 \cdot A \sin(\omega t + \phi) $$

Dimostrazione

La forza elastica è una forza con verso rivolto ad un punto O detto centro e con modulo proporzionale alla distanza dal punto O. Se il centro è l'origine dell'asse x la formula della forza elastica è la seguente $$ \vec{F} = - k \ x \ \vec{u_x} $$ Dove k è una costante positiva detta costante elastica mentre u_x è il versore dell'asse x.

La formula è anche detta legge di Hooke.

$$ \vec{F} = - k \ x \ \vec{u_x} $$

Ad esempio la forza elastica è applicata tramite una molla.

Considero una molla fissata alla parete sinistra.

In condizioni di riposo la molla è lunga l₀ e ha una elasticità k.

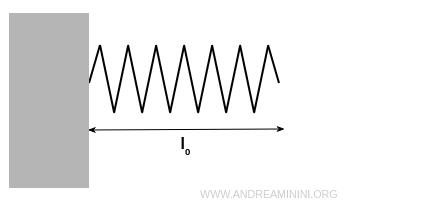
Nota. In questo caso la lunghezza a riposo (l₀) è uguale alla lunghezza corrente (l) della molla. $$ l_0 = l $$ Pertanto, la variabile x è uguale a zero. $$ x = l-l_0 =0 $$

Se tiro la molla verso destra, questa si estende fino a una lunghezza l.

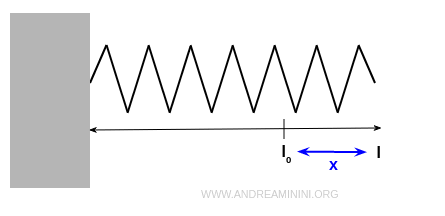
Ora la lunghezza corrente (l) della molla è maggiore rispetto alla lunghezza a riposo (l₀).

$$ x = l - l_0 $$

Si sviluppa una forza oppositiva che cerca di riportare verso sinistra la molla in modo proporzionale alla sua estensione.

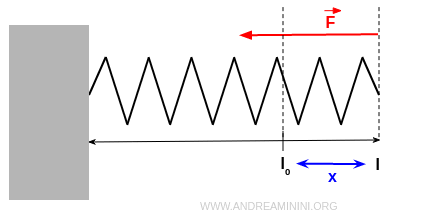
In base alla formula iniziale la forza oppositiva è un vettore di forza F.

$$ \vec{F} = - k \ x \ \vec{u_x} $$

Sapendo che x=l-l₀

$$ \vec{F} = - k \ ( l - l_0 ) \ \vec{u_x} $$

Nel punto B della molla deformata agisce una forza elastica F uguale e contraria alla forza esterna F2 che ho usato per tirare la molla.

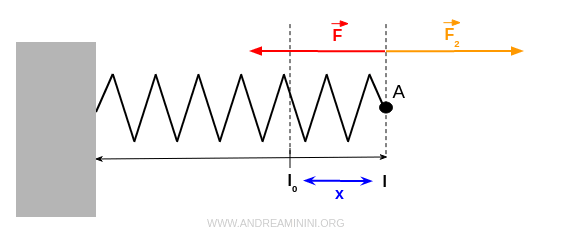
La stessa forza esterna F2=F3 agisce sul punto B in cui la molla è fissata alla parete.

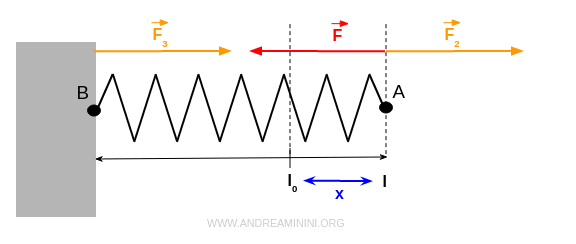
Infine, la parete oppone una forza uguale e contraria F4 per reazione vincolare.

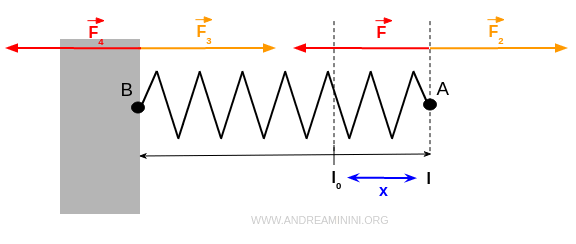
Fin quando mantengo tirata la molla, il sistema di forze agisce sulla molla mantenendola ferma.

Nota. Da questo deduco che se la molla non fosse fissata alla parete, per deformarla di una lunghezza x dovrei applicare due forze esterne uguali e contrarie F4 e F2 agli estremi della molla.

Per misurare le forze prendo come sistema di riferimento il versore u_x che ha origine nel punto O ossia nell'estremo della molla in equilibrio statico.

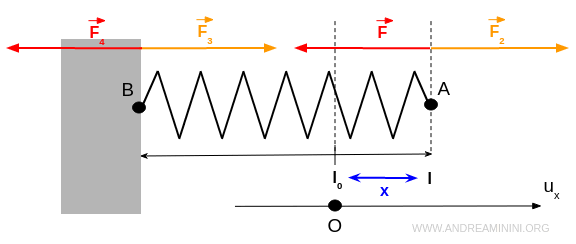
Pertanto le forze F e F4 sono negative perché hanno il verso contrario rispetto al versore u_x.

$$ \vec{F} = - kx \vec{u}_x $$

$$ \vec{F}_4 = - kx \vec{u}_x $$

Viceversa, le forze F2 e F3 sono positive perché hanno lo stesso verso del versore u_x.

$$ \vec{F}_2 = kx \vec{u}_x $$

$$ \vec{F}_3 = kx \vec{u}_x $$

Ora, aggancio all'estremità A un oggetto di massa m e tiro la molla verso destra deformandola fino a x₀.

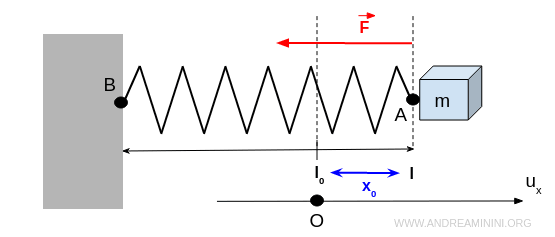
All'estremità B la molla è fissata alla parete.

Quindi, sulla molla si sviluppa una forza di rientro verso sinistra pari a

$$ \vec{F} = - kx \vec{u}_x $$

Dove x è inizialmente x=x₀.

Sapendo che la forza è F=m·a

$$ m \cdot \vec{a} = - kx \vec{u}_x $$

Ora, sapendo che l'accelerazione è la derivata seconda della legge oraria a=d²x(t)/dt² e x=x(t) è la legge del moto.

$$ m \cdot \frac{d^2x(t)}{dt^2} = - kx(t) \vec{u}_x $$

$$ m \cdot \frac{d^2x(t)}{dt^2} + kx(t) \vec{u}_x = 0 $$

$$ \frac{d^2x(t)}{dt^2} + \frac{k}{m} x(t) \vec{u}_x = 0 $$

Questa è un'equazione differenziale omogenea lineare del secondo ordine con coefficienti costanti.

La soluzione dell'equazione differenziale è la legge del moto.

$$ x(t) = A \sin ( \omega t + \phi ) $$

Quest'ultima è la formula del moto armonico semplice su una retta.

Dove A = k/m è l'ampiezza angolare del moto oscillatorio che varia da A a -A.

$$ A = \frac{k}{m} $$

Per trovare la fase iniziale basta verificare le condizioni iniziali del moto quando t=0.

$$ x(t) = A \sin ( \omega \cdot 0 + \phi ) = A \sin ( \phi) $$

Verifica. Per verificarlo basta derivare due volte l'equazione del moto x(t) rispetto al tempo, ricordandosi di applicare la regola di derivazione delle funzione composte. $$ x'(t) = \frac{d \ x(t)}{dt} = \omega \cdot A \cos(\omega t + \phi) $$ $$ x''(t) = \frac{d^{2} x(t)}{dt^2} = - \omega^2 \cdot A \sin(\omega t + \phi) $$ ovvero $$ \frac{d^{2} x(t)}{dt^2} + \omega^2 \cdot A \sin(\omega t + \phi) = 0 $$ Dove $$ \omega^2 = \frac{k}{m} $$ Quindi, le pulsazioni del moto armonico sono $$ \omega = \sqrt{ \frac{k}{m} } $$

Una volta trovata l'equazione del moto x(t), posso ricavare l'equazione della velocità e dell'accelerazione tramite le derivate prima e seconda rispetto al tempo.

$$ x'(t) = v(t) = \frac{d \ x(t)}{dt} = \omega \cdot A \cos(\omega t + \phi) $$

$$ x''(t) = a(t) = \frac{d^{2} x(t)}{dt^2} = - \omega^2 \cdot A \sin(\omega t + \phi) $$

Ora conosco sia x(t)=A sin(ωt+φ) che x''(t)=-ω²A sin(ωt+φ) e posso sostituirli nell'equazione differenziale iniziale.

$$ \frac{d^2x(t)}{dt^2} + \frac{k}{m} x(t) \vec{u}_x = 0 $$

$$ - \omega^2 \cdot A \sin(\omega t + \phi) + \frac{k}{m} A \sin ( \omega t + \phi ) = 0 $$

$$ A \sin(\omega t + \phi) \cdot [ \frac{k}{m} - \omega^2 ] = 0 $$

In questa forma si capisce immediatamente che l'equazione è soddisfatta quando ω² = k/m

$$ \omega^2 = \frac{k}{m} $$

Calcolo la radice quadrata in entrambi i membri e ottengo le pulsazioni del moto.

$$ \sqrt{ \omega^2 } = \sqrt{ \frac{k}{m} } $$

$$ \omega = \sqrt{ \frac{k}{m} } $$

Sapendo che il periodo T del moto oscillatorio è in relazione inversa con le pulsazioni, una volta note queste ultime ottengo anche il periodo.

$$ T = \frac{2 \pi}{\omega} = \frac{2 \pi}{ \sqrt{ \frac{k}{m} } } = 2 \pi \cdot \sqrt{ \frac{m}{k} } $$

E così via.