Centro di massa
Il centro di massa è il punto in cui si può considerare concentrata tutta la massa di un corpo o di un sistema di corpi per studiarne il moto o l'equilibrio delle forze in fisica.
È un concetto astratto ma molto utile in meccanica, perché riduce la complessità di un oggetto reale a un punto fittizio, ma rappresentativo, semplificando l'analisi.
Il centro di massa si muove come se tutta la massa del sistema fosse concentrata in un punto e su questo agisse la risultante delle forze esterne.
Ad esempio, nella dinamica dei sistemi posso studiare il moto traslazionale del corpo come se fosse un solo punto (il centro di massa), semplificando i calcoli.
Dove si trova?
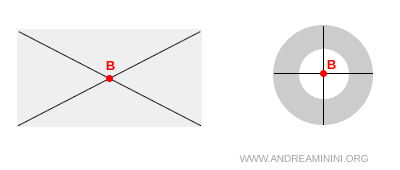
Il centro di massa dipende da come è distribuita la massa all'interno del corpo. In genere è il baricentro.
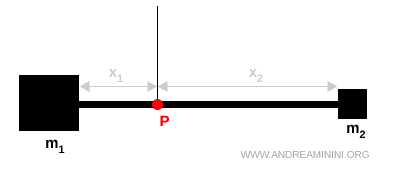
Nel caso semplice di un’asta con due masse $ m_1 $ e $ m_2 $ alle estremità, sospesa in un punto P, l’asta è in equilibrio orizzontale quando i momenti delle forze rispetto a P si compensano:
$$ m_1 x_1 = m_2 x_2 $$
Se questa condizione è soddisfatta, P si trova esattamente nel centro di massa del sistema.
Nota. In questo esempio ho considerato il peso dell’asta trascurabile. Se invece l’asta avesse una massa non trascurabile, occorrerebbe includerla nel calcolo aggiungendo la sua massa e il relativo braccio ai momenti delle altre masse.
Nel caso di un corpo rigido di forma irregolare, il baricentro può essere trovato appendendo il corpo in due punti di sospensione diversi e tracciando le verticali corrispondenti.
Ad esempio, considero una racchetta da tennis. La appendo con un filo nel punto \( P_1 \) e la lascio raggiungere l’equilibrio.
Il centro di massa è uno dei punti sulla verticale passante per \( P_1 \) ma non so ancora qual'è. Quindi traccio la semiretta verticale \( r_1 \) sotto quel punto.
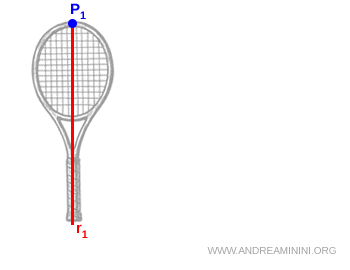
Nota. In equilibrio, la forza peso si scarica lungo la verticale $ r_1 $ e la risultante dei momenti delle forze si annulla. In altre parole, quando è in equilibrio la racchetta non ruota.
Poi appendo la racchetta con un filo da un altro punto di sospensione \( P_2 \) e ripeto la procedura, tracciando la semiretta verticale \( r_2 \).
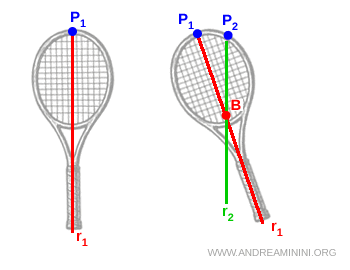
Le due semirette \( r_1 \) e \( r_2 \) si incontrano in un punto unico \( B \).
Quel punto è il centro di massa del corpo rigido.
Un esempio pratico
Considero una cassa di 10 kg su una rampa inclinata.
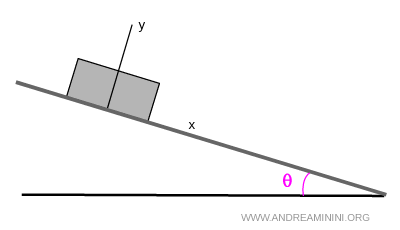
Sulla cassa agiscono diverse forze, ad esempio la forza peso, la reazione vincolare del piano, l'attrito ecc.
Per semplificare l'analisi, prendo come centro di bassa il baricentro $ C $ della figura geometrica e faccio finta che tutte le forze siano applicate su questo punto.
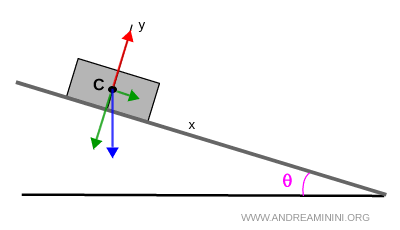
In questo modo il calcolo vettoriale delle forze è più immediato.
Nota. Questo è possibile se accetto l'ipotesi che la massa della cassa (10 kg) sia equamente distribuita in tutto il corpo. Se così non fosse, dovrei calcolare la posizione del centro di massa ponderando la posizione di ogni punto con la relativa massa.
Esempio 2
Una massa da 2 kg si trova a 0 m e una da 3 kg a 4 m su un'asta orizzontale.

In questo caso ci sono due masse, $m_1 = 2 \ kg$ e $m_2 = 3 \ kg$, poste lungo un asse orizzontale a distanze $x_1=0 \ m$ e $x_2=4 \ m$ dall’origine.
Il centro di massa si calcola così:
$$ x_{cm} = \frac{ m_1 x_1 + m_2 x_2 }{ m_1 + m_2 } $$
$$ x_{cm} = \frac{2 \cdot 0 + 3 \cdot 4}{2 + 3} = \frac{12}{5} = 2.4 \, \text{m}
$$
Quindi il centro di massa è più vicino alla massa maggiore, come ci si aspetta intuitivamente.
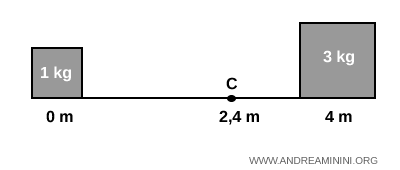
In questo modo, posso studiare il moto di traslazione di questo sistema di corpi come se fosse un unico punto materiale.
E così via.
