La forza di attrito viscoso
La forza di attrito viscoso F è una forza che si oppone al moto di un corpo in modo proporzionale alla velocità (v) del corpo $$ \vec{F} = b \cdot \vec{v} $$ quando il moto si muove in un fluido (gas o liquido). Dove b è un coefficiente che dipende dalla forma dell'oggetto e dalle caratteristiche fisiche del fluido.
Ad esempio, quando un oggetto si muove in un fluido (es. acqua, aria, ecc.) il fluido esercita una resistenza al moto.
Questa resistenza dipende dalla velocità, dalla forma e dalle dimensioni dell'oggetto e dalle caratteristiche del fluido (es. densità, viscosità, ecc.).
In questa pagina tratto il caso più semplice del punto materiale. ossia di un oggetto di forma regolare e di dimensione trascurabile che si muove a basse velocità, senza che ci siano turbolenze o vortici nel fluido (moto laminare).
Essendo una forza contraria, proporzionale alla velocità del corpo, la forza di attrito viscoso si annulla quando il corpo ha velocità nulla (v=0).
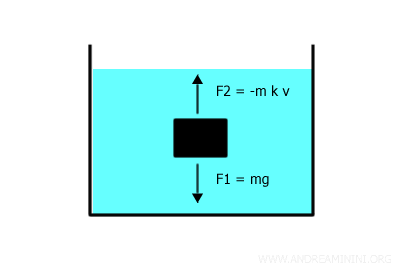
Considerando b=m·k dove m è la massa del corpo, la risultante delle due forze è la seguente:
$$ \vec{F}_1 + \vec{F}_2 = m \cdot \vec{g} - m \cdot k \cdot \vec{v} $$
Dove F1 è la forza peso e F2 è la forza di attrito viscoso che si oppone alla caduta del corpo ossia alla forza peso.
L'accelerazione del corpo in condizioni di gravità terrestre è la seguente
$$ \vec{a} = \vec{g} - k \cdot \vec{v} $$
Proiettando il moto di caduta sull'asse verticale, la formula si può scrivere anche in questo modo
$$ a = g - k \cdot v$$
La velocità è, invece, la seguente:
$$ v = \frac{ g }{k} \cdot (1 - e^{ -kt } ) $$
Analizzando il comportamento asintotico della velocità per t che tende a infinito, la componente e-kt si annulla.
$$ \lim_{t \rightarrow \infty} \frac{ g }{k} \cdot (1 - e^{ -kt } ) = \frac{ g }{k} $$
Pertanto, se il corpo inizialmente era fermo (v=0), la velocità di caduta aumenta sotto la spinta della forza peso ma sempre più lentamente perché la forza di attrito viscoso si oppone.
Il moto uniformemente accelerato si trasforma in un moto uniforme quando la velocità si avvcina al valore g/k
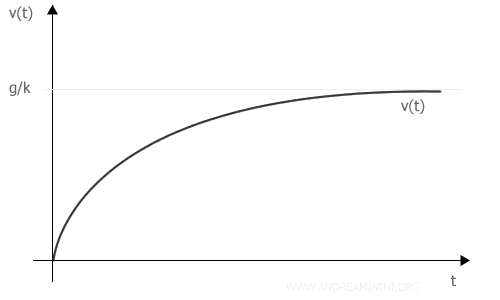
Da questo momento in poi l'accelerazione si annulla a=0 e la velocità di caduta resta costante al valore v=g/k.
In questa situazione asintotica si verifica un equilibrio dinamico tra le due forze F1+F2=0.
La dimostrazione
1] Analisi a una dimensione
Lascio cadere un corpo di massa "m" in un fluido.
Per semplicità considero un punto materiale ossia un corpo privo di forma e dimensioni.
Nell'istante iniziale (t=0) il corpo si trova in posizione x=0 e ha velocità nulla (v=0).
La forza di gravità attira il corpo verso il basso, facendolo accelerare a=g.
$$ \vec{F}_1 = m \cdot \vec{g} $$
Allo spostamento si oppone la forza di attrito viscoso.
$$ \vec{F}_2 = - m \cdot k \cdot \vec{v} $$
Quindi, lo spostamento del corpo è determinato dalle due forze
$$ \vec{F}_1 + \vec{F}_2 = m \cdot \vec{g} - m \cdot k \cdot \vec{v} $$
In questo caso la costante b=mk
Metto in evidenza la massa (m)
$$ \vec{F}_1 + \vec{F}_2 = m \cdot ( \vec{g} - k \cdot \vec{v} ) $$
Sapendo che inizialmente la velocità è nulla kv=0
$$ \vec{F}_1 + \vec{F}_2 = m \cdot ( \vec{g} - k \cdot \vec{v} ) = m \cdot ( \vec{g} - k \cdot \vec{0} ) $$
$$ \vec{F}_1 + \vec{F}_2 = m \cdot ( \vec{g} - k \cdot \vec{v} ) = m \cdot ( \vec{g} - 0 ) $$
$$ \vec{F}_1 + \vec{F}_2 = m \cdot ( \vec{g} - k \cdot \vec{v} ) = m \cdot \vec{g} $$
Inoltre, il vettore gravità rappresenta il vettore accelerazione a=g
$$ \vec{F}_1 + \vec{F}_2 = m \cdot ( \vec{g} - k \cdot \vec{v} ) = m \cdot \vec{a} $$
Ne consegue che il vettore accelerazione è a=g-kv
$$ \vec{a} = \vec{g} - k \cdot \vec{v} $$
Sapendo che l'accelerazione è la derivata della velocità rispetto al tempo a=dv/dt
$$ \frac{ d \ \vec{v}}{dt} = \vec{g} - k \cdot \vec{v} $$
Per ottenere la velocità integro entrambi i membri dell'equazione rispetto al tempo (t)
$$ \int \frac{ d \ \vec{v}}{dt} \ dt = \int \ \vec{g} - k \cdot \vec{v} \ dt $$
$$ \vec{v} = \int \ \vec{g} - k \cdot \vec{v} \ dt $$
Ora per risolvere l'integrale utilizzo il metodo della separazione delle variabili sapendo che dv/dt=g-kv
$$ \frac{ d \ \vec{v}}{dt} = \vec{g} - k \cdot \vec{v} $$
$$ \frac{ d \ \vec{v}}{ \vec{g} - k \cdot \vec{v} } = dt $$
Integro entrambi i membri per le rispettive variabili
$$ \int_0^v \frac{ d \ \vec{v}}{ \vec{g} - k \cdot \vec{v} } = \int_0^t dt $$
$$ \int_0^v \frac{ 1 }{ \vec{g} - k \cdot \vec{v} } \ d \ \vec{v} = \int_0^t dt $$
Il secondo integrale è facile, l'integrale ∫1 dt=t che nell'intervallo di integrazione da 0 a t è [t-0]=t
$$ \int_0^v \frac{ 1 }{ \vec{g} - k \cdot \vec{v} } \ d \ \vec{v} = t $$
Per risolvere il primo integrale introduco una variabile ausiliaria u=g-kv
$$ \int_0^v \frac{ 1 }{ u } \ d \ \vec{v} = t $$
Poi calcolo il differenziale di entrambi i membri
$$ du=(g-kv) dv $$
$$ du= -k \ dv $$
$$ \frac{du}{-k}= dv $$
Sostituisco dv = 1/(-k) dv nell'integrale
$$ \int_0^v \frac{ 1 }{ u } \cdot ( - \frac{1}{k} ) \ du = t $$
Poiché k è una costante, può uscire dall'integrale
$$ - \frac{1}{k} \cdot \int_0^v \frac{ 1 }{ u } \ du = t $$
Ora l'integrale è elementare ∫u=log(u)
$$ - \frac{1}{k} \cdot [ \log |u| ]_0^v = t $$
Sapendo che u=g-kv
$$ - \frac{1}{k} \cdot [ \log | \vec{g} - k \cdot \vec{v} | ]_0^v = t $$
$$ - \frac{1}{k} \cdot (-k) \cdot [ \log | \vec{g} - k \cdot \vec{v} | ]_0^v = t \cdot (-k) $$
$$ [ \log | \vec{g} - k \cdot \vec{v} | ]_0^v = -kt $$
$$ \log ( \vec{g} - k \cdot \vec{v} ) - \log( \vec{g} ) = -kt $$
Applico una proprietà dei logaritmi, in base al quale la differenza tra due logaritmi è uguale al logaritmo del rapporto.
$$ \log \frac{ \vec{g} - k \cdot \vec{v} }{ \vec{g} } = -kt $$
Per semplificare, calcolo l'esponenziale in entrambi i membri
$$ e^{ \log \frac{ \vec{g} - k \cdot \vec{v} }{ \vec{g} } } = e^{ -kt } $$
$$ \frac{ \vec{g} - k \cdot \vec{v} }{ \vec{g} } = e^{ -kt } $$
Infine, ricavo il vettore velocità da tutto il resto
$$ \vec{g} - k \cdot \vec{v} = \vec{g} e^{ -kt } $$
$$ - k \cdot \vec{v} = \vec{g} e^{ -kt } - \vec{g} $$
$$ k \cdot \vec{v} = \vec{g} - \vec{g} e^{ -kt } $$
$$ k \cdot \vec{v} = \vec{g} \cdot (1 - e^{ -kt } ) $$
$$ \vec{v} = \frac{ \vec{g} \cdot (1 - e^{ -kt } ) }{k} $$
$$ \vec{v} = \frac{ \vec{g} }{k} \cdot (1 - e^{ -kt } ) $$
2] Analisi a due dimensioni (x,y)
In questa seconda analisi considero entrambi gli assi x e y del piano.
L'equazione del moto del corpo F=ma è la risultante delle due forze
$$ m \cdot \vec{a} = \vec{F_1} + \vec{F_2} $$
Dove F1 è la forza peso
$$ \vec{F_1} = m \cdot \vec{a} = m \cdot \vec{g} $$
mentre F2 è la forza di attrito viscoso che si oppone al moto
$$ \vec{F_2} = - b \cdot \vec{v} $$
Peranto, l'equazione del moto è la seguente:
$$ m \cdot \vec{a} = \vec{F_1} + \vec{F_2} $$
$$ m \cdot \vec{a} = m \cdot \vec{g} - b \cdot \vec{v} $$
Sapendo che l'accelerazione (a) è la derivata della velocità (v) sostituisco a=dv/dt
$$ m \cdot \frac{ \vec{v} }{dt} = m \cdot \vec{g} - b \cdot \vec{v} $$
Proietto le grandezze vettoriali sugli assi x e y
$$ \begin{cases} - b \cdot v_x = m \cdot \frac{dv_x}{dt} \\ \\ -mg-bv_y = m \cdot \frac{dv_y}{dt} \end{cases} $$
Divido entrambi i membri delle equazioni per b
$$ \begin{cases} - b \cdot v_x \cdot \frac{1}{b} = m \cdot \frac{dv_x}{dt} \cdot \frac{1}{b} \\ \\ -mg-bv_y \cdot \frac{1}{b} = m \cdot \frac{dv_y}{dt} \cdot \frac{1}{b} \end{cases} $$
$$ \begin{cases} - v_x = \frac{m}{b} \cdot \frac{dv_x}{dt} \\ \\ - \frac{mg}{b} -v_y = \frac{m}{b} \cdot \frac{dv_y}{dt} \end{cases} $$
$$ \begin{cases} v_x = - \frac{m}{b} \cdot \frac{dv_x}{dt} \\ \\ \frac{mg}{b} + v_y = - \frac{m}{b} \cdot \frac{dv_y}{dt} \end{cases} $$
E così via
