Esercizio di fisica 1

Tre scatole di massa 5,0 kg, 3,0 kg e 2,0 kg sono impilate l’una sull’altra e appoggiate su un tavolo. Quanto vale la forza normale esercitata dal tavolo?

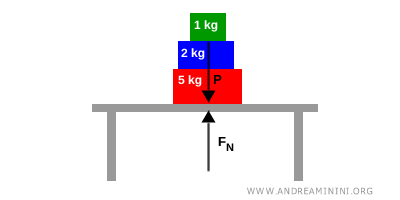
La reazione vincolare del tavolo si adegua, entro un certo limite, al peso degli oggetti. Quindi, la forza normale sarà uguale alla forza peso dei tre oggetti.

Per prima cosa, calcolo la forza peso in newton (N) delle scatole usando la formula della forza peso $ P=mg $ dove $ m $ è la massa e $ g = 9,81 \ N/kg $ è l'accelerazione di gravità.

In questo caso la massa delle tre scatole è 5,0 kg + 3,0 kg + 2,0 kg

$$ m = 5,0 \ kg + 3,0 \ kg + 2,0 \ kg = 10,0 \ kg $$

Sostituisco la massa nella forza peso.

$$ P = mg = 10,0 \ kg \cdot 9,81 \ N/kg = 98,1 \ N  $$

Poiché la reazione vincolare del tavolo si adegua al peso, nel verso opposto $ \vec{P} = - \vec{F}_N $ , la sua intensità è uguale a quella del peso $ F_N = P $.

$$ F_N = 98,1 \ N $$

Quindi, la forza normale del tavolo è 98,1 N.

Cosa succede se aggiungo un altra scatola di 1 kg?

Per ipotesi, aggiungo un'altra scatola di 1 kg sopra le precedenti. La forza normale del tavolo è sempre la stessa?

Se metto un’altra scatola da 1 kg sopra, la massa totale diventa 11 kg, e allora la forza peso aumenta.

$$ m_{\text{totale}} = 5{,}0 + 3{,}0 + 2{,}0 + 1{,}0 = 11{,}0 \ \text{kg} $$

Pertanto, la forza normale del tavolo non è più la stessa. Che genio eh...

$$ F_N = P = mg = 11{,}0 \cdot 9{,}81 = 107{,}91 \ \text{N} $$

Adesso è 107,91 N, perché c'è più massa sopra, quindi più peso, e il tavolo deve spingere di più verso l’alto.

Nota. Ovviamente questo processo non vale all'infinito. Se la forza peso supera la resistenza massima del tavolo, la reazione vincolare non può più bilanciare e si spacca in due come una noce. Ad esempio, se la resistenza massima del tavolo è 100 kg, oltre questo limite il tavolo si rompe. Quindi, non posso mettere un frigorifero e una lavatrice sopra il tavolo...

Cosa succede se il piano è inclinato di 15°?

Per ipotesi, il tavolo è in pendenza di 15° rispetto alla terra e le tre scatole restano ferme, la forza normale del tavolo è sempre la stessa?

 

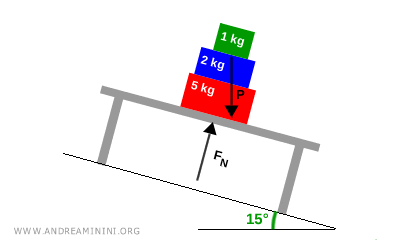
Se le scatole non si muovono, questo significa che l’attrito statico è sufficiente a contrastare la tendenza delle scatole a scivolare lungo il piano.

In questo caso, la forza normale esercitata dal tavolo non è più uguale a quella di prima (cioè col tavolo orizzontale), perché la forza peso resta verticale, mentre la normale è perpendicolare alla superficie inclinata.

Le due forze non sono più direttamente opposte, quindi devo scomporre il vettore della forza peso in due componenti:

• una componente perpendicolare $ P_y $ al piano che viene bilanciata dalla normale $ F_N $
• una componente parallela $ P_x $  al piano che viene contrastata dall’attrito statico $ A_x $

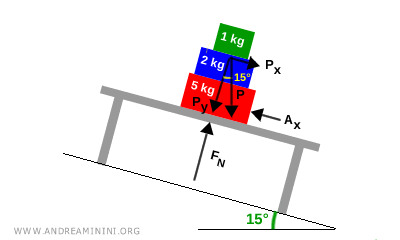
L'angolo tra i vettori $ \vec{P_y} $ e $ \vec{P} $ è uguale all'inclinazione del piano ossia $ 15° $

Per calcolare la lunghezza di $ \vec{P_y} $ posso usare la formula del coseno

$$ \cos \theta = \frac{ \text{cateto adiacente} }{ \text{ipotenusa} } $$

In questo caso $ \theta = 15° $, il cateto adiacente è $ P_y $ e l'ipotenusa è $ P $.

$$ \cos 15° = \frac{ P_y }{ P } $$

$$ P_y = P \cdot \cos 15° $$

Dove $\cos(15^\circ) \approx 0{,}9659$

$$ P_y = P \cdot 0,9659 $$

La forza peso è sempre la stessa.

$$ P_y = mg \cdot 0,9659 $$

$$ P_y = 10 \ kg \cdot 9{,}81 \ N/kg \cdot 0,9659 $$

$$ P_y = 94,7 \ N $$

Quindi, la forza normale diminuisce perché si oppone a $ P_y $ con la stessa intensità:

$$ F_N = P_y  $$

Pertanto, la forza normale del tavolo è circa 94,7 N.

$$ F_N \approx 94,7 \ N $$

In conclusione, la forza normale non è più la stessa. È un po’ più bassa, perché spinge perpendicolarmente al piano e ora non è più dritta contro la forza peso.

E così via.