Risultante delle forze
Quando su un punto materiale agiscono più forze contemporaneamente F1, F2, ... Fn, l'effetto sul moto del punto equivale a quello di un'unica forza R composta dalla somma vettoriale delle forze, detta risultante delle forze. $$ \vec{R} = \vec{F_1}+\vec{F_2} + ... + \vec{F_n} $$
Le componenti della risultante delle forze si ottengono sommando le componenti delle singole forze.
$$ R_x = F_{1x} + F_{2x} + ... + F_{nx} $$
$$ R_y = F_{1y} + F_{2y} + ... + F_{ny} $$
$$ R_z = F_{1z} + F_{2z} + ... + F_{nz}$$
Dove ogni forza è un vettore nello spazio a tre dimensioni (x,y,z)
Nota. Nel caso in cui le forze agiscano sul piano i vettori sono a due dimensioni (x,y). Il ragionamento è comunque sempre lo stesso. La risultante delle forze è la somma vettoriale delle forze.
Un esempio pratico
Un punto materiale P si trova sul piano nella posizione (0,0)
Sul punto materiale agiscono due forze F1 e F2
$$ \vec{F1} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} $$
$$ \vec{F2} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$
Dal punto di vista grafico
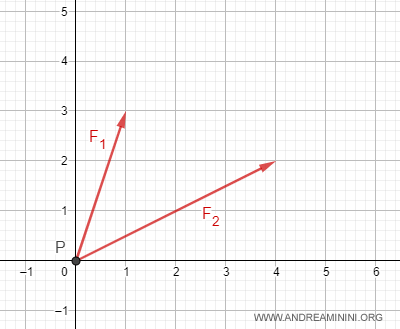
La risultante delle forze R è la somma vettoriale delle due forze F1+F2
$$ R = \vec{F1} + \vec{F2} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} + \begin{pmatrix} 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 1+4 \\ 3+2 \end{pmatrix} = \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$
Pertanto, il punto materiale si sposta sul piano dalle coordinate (0,0) nel verso, nella direzione e con l'intensità (modulo) del vettore R=F1+F2.
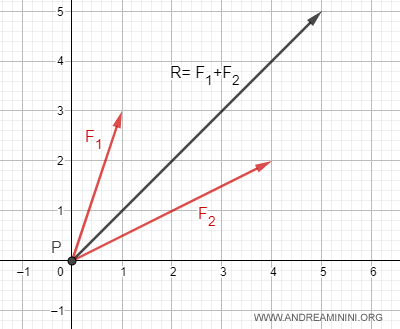
Nota. La direzione della risultante delle forze è la retta in cui si trova il vettore R. Il verso del vettore è indicato dalla freccia. L'intensità (o modulo) del vettore è la lunghezza della freccia. Per calcolare la lunghezza della freccia utilizzo il teorema di Pitagora. $$ |R| = \sqrt{5^2+5^2} = \sqrt{50} ≅ 7,07 $$ In genere per indicare il modulo del vettore si scrive il nome del vettore tra due barre verticali |R|.
L'equilibrio statico
L'equilibrio statico è un caso particolare che si verifica quando la risultante delle forze è nulla R=0 in presenza di forze non nulle. $$ \vec{R} = \vec{F_1}+\vec{F_2} + ... + \vec{F_n} = \vec{0} $$
Ad esempio, questo accade quando le forze sono uguali ma opposte.
$$ \vec{R} = \vec{F_1}+\vec{F_2} = \vec{0} $$
Dove F1 e F2 sono due vettori opposti.
$$ \vec{F_1} = - \vec{F_2} $$
Dal punto di vista grafico sul punto materiale agiscono due forze di pari intensità che condividono la stessa direzione ma hanno verso opposto.
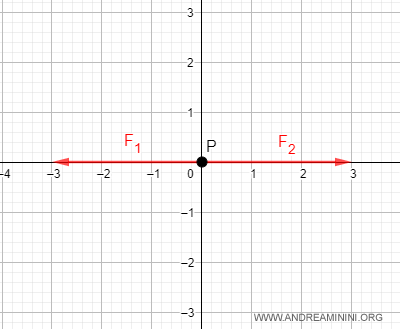
Nell'esempio precedente il punto materiale si trova alle coordinate (0;0)
La risultante delle forze è un vettore nullo.
$$ \vec{R} = \vec{F_1} + \vec{F_2} = \begin{pmatrix} -3 \\ 0 \end{pmatrix} + \begin{pmatrix} 3 \\ 0 \end{pmatrix} = \begin{pmatrix} -3+3 \\ 0+0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$
Quindi il punto resta alle coordinate (0;0), non si muove pur essendo sottoposto a due forze.
Nota. L'intensità della forza è il modulo ossia la lunghezza della freccia. La direzione è la retta in cui si trovano i vettori. Il verso è il segno algebrico del vettore.
In questo caso la somma delle componenti dei due vettori sugli assi del piano è nulla.
$$ F_{1x} + F_{2x} = -3 + 3 = 0 $$
$$ F_{1y} + F_{2y} = 0 + 0 = 0 $$
Pertanto, l'assenza di una forza agente non vuol dire necessariamente che il punto materiale non interagisca con l'ambiente esterno.
Nota. La somma vettoriale delle forze è un vettore. Il risultato è un vettore nullo. $$ \vec{F_1}+\vec{F_2} = \vec{0} $$ La somma delle componenti dei vettori, invece, è una somma tra numeri scalari perché le componenti (x,y) sono numeri reali. Pertanto, il risultato è zero. $$ F_{1x} + F_{2x} = -3 + 3 = 0 $$ $$ F_{1y} + F_{2y} = 0 + 0 = 0 $$
Cosa accade se le forze sono più di due?
Se le forze sono più di due vale sempre lo stesso ragionamento.
Il punto materiale è in equilibrio statico se la somma vettoriale delle forze (vettori) è un vettore nullo.
$$ \vec{R} = \vec{F_1}+\vec{F_2}+\vec{F_3} = \vec{0} $$
Ad esempio, sul punto P agiscono tre forze F1, F2 e F3
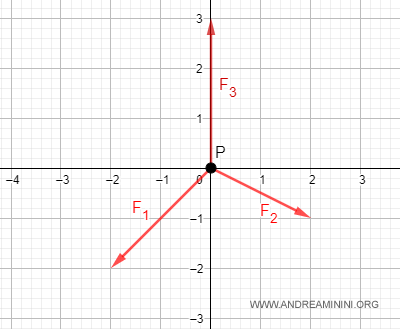
La somma vettoriale delle tre forze è un vettore nullo.
$$ \vec{R} = \vec{F_1} + \vec{F_2} + \vec{F_3} = \begin{pmatrix} -2 \\ -2 \end{pmatrix} + \begin{pmatrix} 2 \\ -1 \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \end{pmatrix} = \begin{pmatrix} -2+2+0 \\ -2+-1+3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$
Quindi, il punto si trova in equilibrio statico. Non si muove.
Nota. Nel caso di tre forze in equilibrio statico sul piano, i vettori hanno un modulo uguale al modulo della risultante degli altri due vettori. Ad esempio, la lunghezza (modulo) del vettore F3 è uguale a |F3|=3. Essendo un equilibrio statico, anche la lunghezza (modulo) della risultante degli altri due vettori è uguale a |F1+F2|=3. Dal punto di vista grafico la risultante degli altri due vettori F1+F2 è un vettore opposto rispetto al vettore F3, ha la stessa lunghezza (modulo) e direzione ma verso opposto.
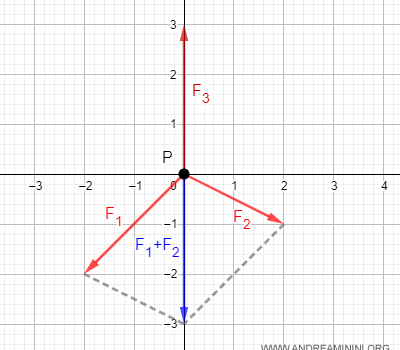
In generale, se concateno geometricamente tre o più vettori tra loro (in qualsiasi combinazione) in equilibrio statico la somma algebrica forma una poligonale chiusa. Ad esempio, la concatenazione F3+F2+F1 forma un triangolo.
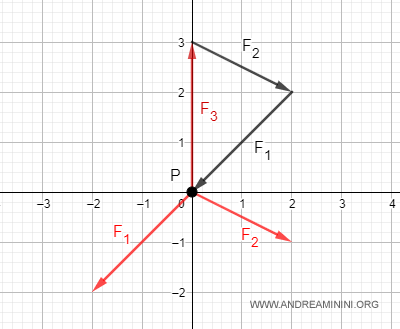
E così via.
