Momento di una coppia di forze
Il momento di una coppia è l’effetto rotatorio prodotto da una delle due forze per la distanza tra le loro linee d’azione, e si calcola con $$ M = F \cdot d $$ Dove $ F $ è l'intensità di una sola delle due forze e $ d $ è la distanza tra le linee d'azione.
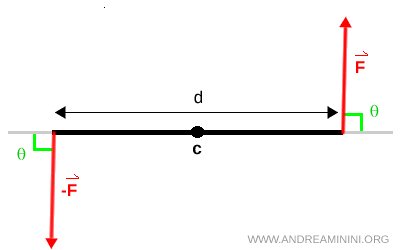
Se le forze non agiscono perpendicolarmente alla congiungente, la formula diventa $$ M = F \cdot d \cdot \sin\theta $$ dove $ \theta $ è l’angolo tra forza e congiungente.
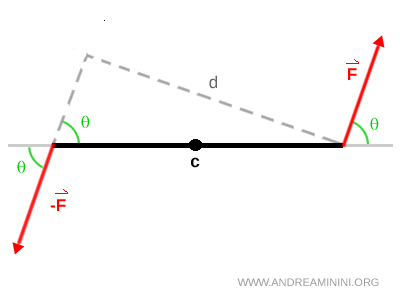
Una coppia di forze è un sistema di due forze uguali, parallele e opposte che non producono traslazione ma solo una rotazione.
In una coppia due forze sono uguali in intensità, con le linee di azione parallele, separate e opposte in verso.
La distanza tra le linee d’azione è detta braccio della coppia.
Le due forze, pur annullandosi tra loro come risultante, generano un effetto rotatorio perché agiscono ai due lati dell’oggetto, in versi opposti, senza alcuna traslazione.
Nota. Come accade per il momento di una forza, il segno del momento della coppia è positivo ( $ M > 0 $ ) se causa una rotazione antioraria, è negativo ( $ M < 0 $ ) se causa una rotazione oraria. Se $ M=0 $ non si verifica nessuna rotazione del corpo rigido.
Esempio
Afferro una valvola idraulica con due mani, la mano sinistra spinge verso il basso, la mano destra verso l'altro con la stessa forza $ F = 8 \ N $.
Ogni mano si trova a $ 10 \ cm $ dal centro della valvola e spingono perpendicolarmente al braccio delle forze.
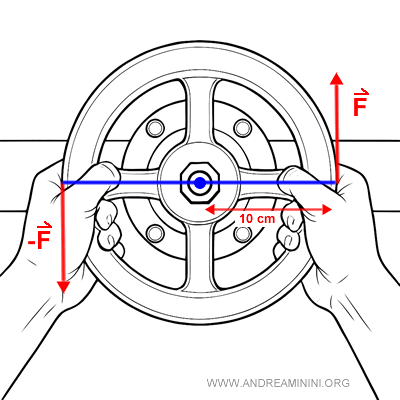
Questo gesto genera un momento di coppia, ossia un effetto rotatorio.
$$ M = F \cdot d $$
La distanza tra le forze è quindi $ 10 \ cm + 10 \ cm = 20 \ cm $.
$$ M = F \cdot ( 20 \ cm ) $$
Converto in mertri
$$ M = F \cdot ( 0.2 \ m ) $$
Considero una sola delle due forze.
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) $$
$$ M = 1.6 \ Nm $$
Quindi, il momento della coppia di forze è 1.6.
Esempio 2
Considero l'esempio precedente, ora però le forze spingono con un angolo di 110° rispetto al braccio. Come cambia il momento?.
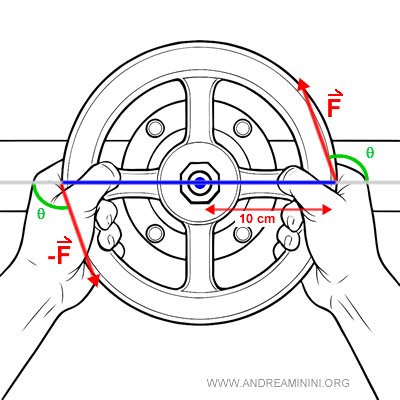
Gli altri dati sono invariati, ogni mano spinge con un'intensità di $ 8 \ N $ e si trova a $ 10 \ cm $ dal centro della valvola.
In questo caso, per calcolare il momento delle forze devo considerare anche l'angolo $ \theta = 110° $.
$$ M = F \cdot d \cdot \sin\theta $$
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot \sin 110° $$
Poiché il seno si trova nel secondo quadrante posso usare la formula equivalente $ \sin \theta = \sin ( 180°- \theta ) $ ovvero $ \sin 110° = \sin (180°-110°) = \sin ( 70° ) $
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot \sin 70° $$
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot 0.94 $$
$$ M \approx 1.50 \ Nm $$
Il momento delle coppie è leggermente inferiore rispetto all'esempio precedente, dove le forze agivano perpendicolarmente al diametro della valvola.
E così via.
