Le leve in fisica
Una leva è un corpo rigido che può ruotare attorno a un punto fisso, detto fulcro. Su una leva agiscono sempre tre elementi fondamentali:
- il fulcro, cioè il punto attorno al quale la leva ruota;
- la forza motrice \( F_M \), cioè la forza applicata per ottenere il movimento;
- la forza resistente \( F_R \), cioè la forza da vincere, spesso il peso di un oggetto.
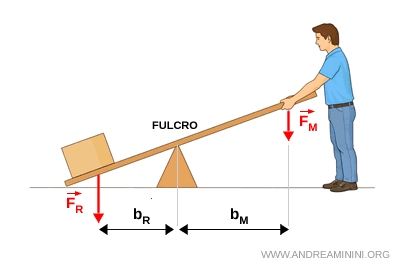
A ciascuna forza è associato un braccio, che è la distanza tra il fulcro e il punto di applicazione della forza. Si indicano con:
- \( b_M \) il braccio della forza motrice
- \( b_R \) il braccio della forza resistente
La forza motrice \( F_M \) e la forza resistente \( F_R \) sono bilanciate dalla reazione vincolare del fulcro.
Per ottenere l'equilibrio è necessario che anche il momento totale delle forze sia nullo, scegliendo il fulcro come centro di rotazione.
$$ b_R F_R = b_M F_M $$
Questa relazione mostra che l’intensità di una forza può essere ridotta aumentando il suo braccio, oppure aumentata se il braccio è più corto.
Ad esempio, per sollevare un oggetto pesante è conveniente applicare la forza motrice \( F_M \) il più lontano possibile dal fulcro, in modo da aumentare il suo braccio \( b_M \) e ridurre l’intensità della forza necessaria.
Quindi, dal punto di vista pratico le leve sono semplici macchine che permettono di equilibrare o amplificare una forza per sollevare, spostare o vincere una resistenza.
Un esempio pratico
Considero una leva in equilibrio per cui vale:
$$ b_R F_R = b_M F_M $$
Supponiamo che la forza resistente sia
$$ F_R = 100\ \text{N} $$
e che il suo braccio sia
$$ b_R = 0.20\ \text{m} $$
Se la forza motrice è applicata a un metro dal fulcro $ b_M = 1.00\ \text{m} $, la forza motrice necessaria è:
$$ F_M = \frac{b_R}{b_M} F_R = \frac{0.20}{1.00} \cdot 100 = 20\ \text{N} $$
La forza motrice è quindi molto più piccola della forza resistente.
Nota. Se invece la forza motrice fosse applicata da 10 centimetri, ossia $ b_M = 0.10\ \text{m} $, la forza motrice necessaria sarebbe molto più alta $$ F_M = \frac{0.20}{0.10} \cdot 100 = 200\ \text{N} $$ In questo caso la forza motrice deve essere maggiore della forza resistente.
Pertanto, a parità di forza resistente, aumentare il braccio della forza motrice riduce la forza necessaria, mentre accorciare il braccio la aumenta.
Leve vantaggiose, svantaggiose e indifferenti
In base al confronto tra i bracci, una leva può essere vantaggiosa, svantaggiosa o indifferente.
- Leva vantaggiosa
Una leva è vantaggiosa se il braccio della forza motrice è maggiore del braccio della forza resistente $$
b_M > b_R $$ In questo caso, per mantenere la leva in equilibrio è sufficiente una forza motrice minore della forza resistente $$ F_M < F_R $$ La leva consente quindi di vincere una forza grande applicando una forza più piccola.
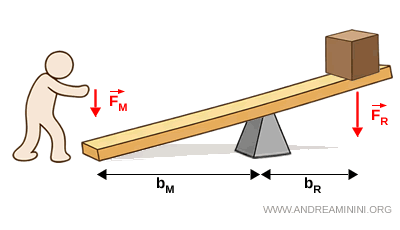
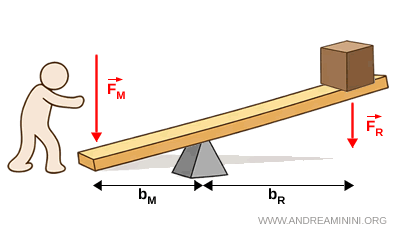
- Leva svantaggiosa
Una leva è svantaggiosa se il braccio della forza motrice è minore del braccio della forza resistente $$ b_M < b_R
$$ In questo caso, per l’equilibrio è necessaria una forza motrice maggiore della forza resistente $$ F_M > F_R
$$ La leva non riduce la forza, ma può essere utile per ottenere maggiore precisione o velocità di movimento.
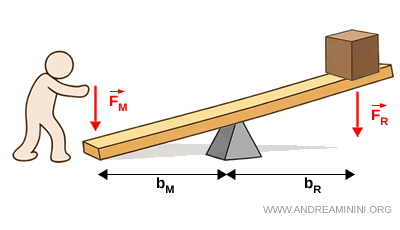
- Leva indifferente
Una leva è indifferente se i due bracci sono uguali $$ b_M = b_R $$ In questo caso la forza motrice è uguale alla forza resistente $$ F_M = F_R $$ La leva non fornisce né vantaggio né svantaggio in termini di intensità della forza.
Tipi di leve
Le leve si classificano in tre generi, in base alla posizione relativa di fulcro, forza motrice e forza resistente.
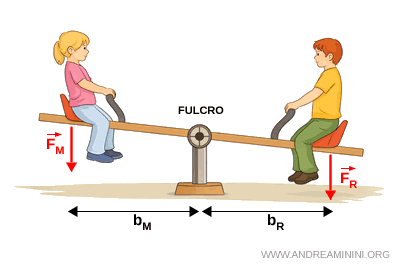
- Leva di primo genere
Il fulcro si trova tra la forza motrice e la forza resistente. Può essere vantaggiosa, svantaggiosa o indifferente. Ad esempio, le forbici o un'altalena.
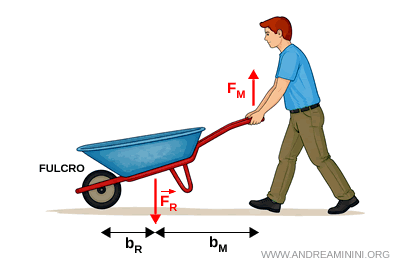
- Leva di secondo genere
La forza resistente si trova tra il fulcro e la forza motrice. È sempre vantaggiosa. Ad esempio, una carriola, lo schiaccianoci, l'apribottiglie.
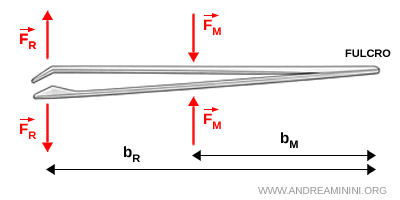
- Leva di terzo genere
- La forza motrice si trova tra il fulcro e la forza resistente. È sempre svantaggiosa perché il braccio $ b_R $ è più lungo del braccio $ b_M $, ma permette movimenti rapidi e precisi. Ad esempio, le pinzette.
Questi tre generi di leve mostrano come la posizione delle forze sia spesso più importante della loro intensità.
Con un corretto uso dei bracci, una forza piccola può vincerne una molto più grande.
Un esercizio pratico
Un operaio utilizza una leva rigida per sollevare una cassa che ha una massa di 75 kg.
La cassa è posta a 0.40 m dal fulcro e l’operaio applica la forza motrice all’estremità opposta della leva, a 1.60 m dal fulcro.
I dati del problema sono:
- \( b_R = 0.40 \ \text{m} \)
- \( b_M = 1.60 \ \text{m} \)
- \( m = 75 \ \text{kg} \)
Qual è l’intensità della forza resistente esercitata dalla cassa?
La forza resistente è il peso della cassa:
$$ F_R = P = mg $$
La massa è $ m=75 \ kg $ l'accelerazione di gravità \( g = 9.8 \ \text{N/kg} \)
$$ F_R = 75 \ ( \text{kg} ) \cdot 9.8 \ ( \text{N/kg} ) = 735 \ \text{N} $$
Quindi, la forza resistente della cassa è:
$$ F_R = 735 \ \text{N} $$
Qual è la forza motrice che l’operaio deve applicare per mantenere la leva in equilibrio?
La condizione di equilibrio della leva è:
$$ b_R F_R = b_M F_M $$
Ricavo \( F_M \):
$$ F_M = \frac{b_R}{b_M} F_R = \frac{0.40}{1.60} \cdot 735 $$
$$ F_M = 0.25 \cdot 735 = 183.75 \ \text{N} \approx 184 \ \text{N} $$
Quindi, la forza motrice necessaria in equilibrio è:
$$ F_M \approx 184 \ \text{N} $$
Di che tipo di leva si tratta?
Una leva è vantaggiosa se \( b_M > b_R \)
In questo caso ho $ b_M = 1.60 \ m $ e $ b_R = 0.40 \ m $. Quindi la leva è vantaggiosa.
Inoltre il vantaggio meccanico vale:
$$ \frac{F_R}{F_M} = \frac{b_M}{b_R} = \frac{1.60}{0.40} = 4 $$
Questo vuol dire che la forza motrice è circa 4 volte più piccola della resistente.
Esercizio 2
Un sacco con una massa di $ m=200 \ kg $ si trova a un'estremità di una leva del primo genere, all'altra estremità un operaio applica una forza motrice di $ F_M=200 \ N $.
A quale distanza si trova il fulcro in condizioni di equilibrio?
La condizione di equilibrio della leva è:
$$ b_R F_R = b_M F_M $$
So già che la forza motrice è $ F_M = 200 \ N $
$$ b_R F_R = b_M \cdot 200 \ ( N ) $$
La forza resistente è la forza peso del masso.
$$ F_R = mg = 200 \ (kg) \cdot 9.81 \ (N/kg) = 1962 N $$
Sostituisco $ F_R = 1962 \ N $ nella condizione di equilibrio.
$$ b_R \cdot ( 1962 \ N ) = b_M \cdot 200 \ ( N ) $$
$$ b_R \cdot 1962 = b_M \cdot 200 $$
Ricavo $ b_R $
$$ b_R = \frac{ b_M \cdot 200}{1962 } $$
$$ b_R = b_M \cdot 0.102 $$
Sapendo che la leva è lunga $ L=b_R+b_M= 3.00 \ m $, posso sostituire $ b_M = 3.00 \ m - b_R $
$$ b_R = (3.00 \ m - b_R) \cdot 0.102 $$
$$ b_R = 0.306 \ m - b_R \cdot 0.102 $$
$$ b_R + b_R \cdot 0.102= 0.306 \ m $$
$$ b_R \cdot (1+ 0.102) = 0.306 \ m $$
$$ b_R \cdot (1.102) = 0.306 \ m $$
$$ b_R = \frac{0.306 \ m}{1.102} $$
$$ b_R \approx 0.28 \ m $$
In condizioni di equilibio il fulcro deve trovarsi $ a 0.28 \ m $ dal sacco.
Per completezza, il braccio della forza motrice è lungo:
$$ b_M = 3.00 - 0.28 = 2.72 \ m $$
La leva è quindi vantaggiosa, perché il braccio motrice è molto più lungo del braccio resistente ( $ b_M>b_R $ ).
Esercizio 3
Un apribottiglie lungo 10 cm viene utilizzato per stappare il tappo a corona di una bottiglia.
La distanza tra il fulcro e il punto di contatto sul tappo è di 2 centimetri e il tappo esercita una forza resistente di 100 N.
Quale forza motrice va applicata all'estremità dell'apribottiglie?

Per semplificità uso il sistema di riferimento xy facendo coincidere l'asse x con l'apribottiglie.
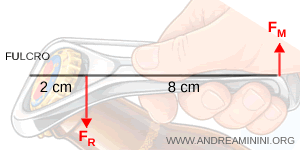
La leva è in equilibrio quando i momenti delle forze rispetto al fulcro si compensano:
$$ b_R F_R = b_M F_M $$
Sapendo che $ b_R = 2 \ cm = 0.02 \ m $, $ b_M = ( 10 - 2 ) \ cm = 0.08 \ m $ e $ F_R = 100 \ N $
$$ ( 0.02 \ m ) \cdot ( 100 \ N ) = (0.08 \ m ) \cdot F_M $$
Semplifico le unità di misura $ m $ in entrambi i lati
$$ 0.02 \cdot ( 100 \ N ) = 0.08 \cdot F_M $$
Quindi, ricavo la forza motrice
$$ F_M = \frac{ 0.02 \cdot ( 100 \ N ) }{0.08} = 25 \ N $$
Per stappare la bottiglia è necessario applicare una forza motrice di almeno 25 N.
Nella pratica, la forza applicata deve essere leggermente superiore a questo valore per vincere attriti, deformazioni e perdite meccaniche.
E così via.
